ибо здесь х =

к − np

4 − 800 0,005

0

=

= 0 ;

е =1, так что ошибка

npq

800 0,005 0,995

некоторого промежутка времени t

равна 0,008, найти вероятность то-

го, что за это время произойдет не

Д

олее 10 обрывов.

4. В магазине 10 000 книг. Вероятность продажи каждой из них в

А

течение дня равна 0,8. Какое максимальное число книг будет продано

в течение дня с вероятностью 0,999?

б

и

1. а) P = 0,321; б)

P = 0,244 . 2.

n ≥ 298 . 3.

P = 0,94255 . 4. 8124.

5.100.

С

X примет значение меньше x:

И

F(x) = P(X < x) . Для дискретной слу-

чайной величины функция

F(x) вычисляется

по формуле

Д

F(x) =

∑ Pi , где суммирование ведется по всем значениям i , для к о-

xi <x

торых

xi < x.

А

если ее функ-

Случайная величина X называется непрерывной,

Плотностью распределения непрерывной случайной величины

и

X называется функц я

P(x < X < x + ∆x)

С

′

f (x) =

limб

∆x

= F (x).

∆x→0

Плотность распределения любой случайной величины неотрица-

тельна ( f (x) ≥ 0) и обладает свойством

+∞

∫ f (x)dx =1.

−∞

Функция распределения F(x) выражается через плотность рас-

пределения формулой

x

F(x) =

∫ f (x)dx .

участок от α до β

может быть вычислена по формуле

β

P(α < X < β ) = ∫ f (x) dx .

(2.16)

α

Математическое ожидание mx = M (X ) случайной величины X

вычисляется по формулам:

∞

M (Х ) = ∑ xi Pi

(для дискретной случайной величины);

М(С)=С.

2.

Постоянный множитель можно выносить за знак математиче-

ского ожидания:

А

И

M (СХ ) = СM (Х ).

б

3.

Математическое ожидание суммыДнескольких случайных ве-

личин равно сумме их математических ожиданий:

и

М(Х+ Y+...+Z) = M(X)+ M(Y) +... +M(Z).

4.

Математическое ож дание произведения двух независимых

С

D(CX)=C2D(X).

3. Дисперсия суммы независимых случайных величин равна сум-

ме дисперсий слагаемых:

D(X+Y)=D(X)+D(Y).

4. Дисперсия разности независимых случайных величин равна

сумме дисперсий слагаемых:

И

k

D(X–Y)=D(X)+D(Y).

Средним квадратичным отклонением случайной величины Х

называется корень квадратный из дисперсии σ (X ) =

D(X ).

Начальными

αk

и центральными

µk моментами

k -го порядка

случайной величины

Х

А

αk = M (X ) ;

называются

соответственно

µk

= M (X − mx )k

.

Д

Начальные αk и центральные

µk моменты случайной величины

Х

и

n

P ;

n

(x

− m

)k P (для

вычисляются по формулам

α

k

= ∑ xk

µ

k

=

∑

i

x

С

бi=1

i=1

+∞

дискретной

случайной

величины);

αk

=

xk f (x)dx ;

∫

−∞

µk

= +∞∫ (x − mx )k f (x)dx

(для

непрерывной

случайной величины).

−∞

S X

=

µ3

называется

коэффициентом

асимметрии,

характеризует

σ 3

асимметричность распределения.

EX =

µ4

− 3

называется эксцессом,

характеризует крутость кри-

σ 4

если 0 < x ≤ 1.

Если x ≤ 0 , то X > x всегда и равенство X < x невоз-

можно, т.к. 0 < X < 1. Если x > 1,

то X < x всегда,

т.к.

0 < X < 1. По-

этому F(x) = 0, если x ≤ 0 и F(x) = 1, если x > 1. Таким образом,

0,

если x ≤ 1;

если 0 < x ≤ 1;

F(x) = x,

если х > 1.

1,

Задача 2. Пусть X – число гербов в двух независимых бросаниях

монеты. Х может принимать значения 0, 1, 2, причём

P{x = 0}= P{x= 2}= 1 ; P{x = 1}= 1 .

Д

4

4

2

т.к. X прини-

Поэтому,

если x ≤ 0 , то F(x) = P(−∞ < X < x) = 0,

А

мает только положительные значения: 0,1,2.ИЕсли 0 < x ≤ 1, то

F(x) = P(0 < X < x) = P{x= 0}=

1 ,

F(x) = P(X < x) = P{(x = 0) (x = 1)}= P{x = 0}+ P{x = 1}= 1 + 1 = 3 .

С

б

4 2 4

Т.к. если x пр надлеж т нтервалу

[1;2], то x больше двух значе-

ний случайной величиныи: x = 0 и x = 1.

Если x > 2 , то P{X < x}= 1,

0,

если x ≤ 0;

1

, если 0 < x ≤ 1;

Итак,

4

F(x) =

3

, если 1 < x ≤ 2;

4

если x > 2.

1,

P = P(x = 1) = 0,1;

P = P(x = 2) = 0,9 0,1; P = P(x = 3) = 0,92 0,1;

1

2

3

P = P(x = 4) = 0,93

0,1;

P = P(x = 5) = 0,94

0,1 0,95

= 0,6591,

4

5

ны.

И

Таким образом, ряд распределения будет иметь вид табл.1.

Таблица 1

Х

1

2

3

4

5

р

0,1

0,09

0,081

0,0729

0,6591

А

n

б

0,081Д+ 4 0,0729 + 5 0,6521 = 4,0951;

M (Х ) = ∑ pi xi = 1 0,1 + 2 0,09 + 3

l=1

D(Х ) = М (Х 2 ) − (М (Х ))2

= 1 0,1 + 22 0,09 + 32 0,081 + 42 0,0729 +

+ 52 0,6521 − (4,0951)2

=

1,9881 .

С

Задача 4. Плотность вероятности случайных амплитуд боковой

качки корабля имеет в

д (закон Релея)

и

x

−x2

f (x) =

2a2 (x ≥ 0).

Определить:

a2

а) функцию распределения;

б) математическое ожидание.

Решение

x

. Так как x ≥

0 , то

а) F(x) = ∫

f (x)dx

−∞

x

x

−x2

x

−x2

x

2

x2

2a2 dx =

2a2 d(−

) = 1− 2a2 .

F

(x) = ∫

∫

a2

2a2

0

0

∞ x

2

−x2

∞

π

б) М х

=

хf (x)dx

=

2a

2

dx = a

.

∫

∫

2

2

−∞

0 a

При вычислении воспользовались формулой интегрирования по

частям

b

b

b

∫ udv = u v

− ∫ vdu ,

a

a

a

x

− x2

− x2

И2

где u = x; du = dx; dv =

a2

2a

2 dx; v = − 2a2 .

Д2

Задача 5. Случайная величина Х

имеет плотность

Acos2 x при

х

≤ π ;

f (x) =

А

> π .

0 при

х

Найти:

б

а) коэффициент А;

б) М (Х ) и D(Х ) .

Решение

С

а) Так как все значен я случайной величины Х принадлежат от-

π

,

π

, то

и

резку −

2

2

π

2

f ( x )dx =1,

∫

то есть

−π 2

π

∫2 Acos2 xdx =1,

π 2 1+ cos 2x

−π 2

1

sin 2x

π

π

=1, А =

2

,

A ∫

dx = A(

x

+

)

−π2

=

A

2

2

2

2

π

−π

2

2

то есть

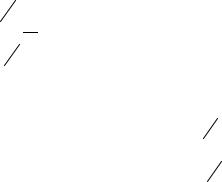
2

cos

2

x при

x

≤

π

;

2

f (x) = π

> π .

0

при

х

2

D(Х ) = M (Х

2

) − (M (Х ))

2

=

π 2

2

x

2

cos

2

xdx =

π 2

−

1

.

∫

12

2

π

−π

2

При вычислении воспользовались формулами:

cos2 x =

1

+ cos 2x

;

в

= u v

в

в

∫ udv

− ∫ vdu.

2

Д

а

а

а

А

Задачи для самостоятельногоИрешения

1. В партии из 10 деталей имеются 8 стандартных. Наудачу ото-

б

браны 2 детали. Составить закон распределения числа стандартных

деталей среди отобранных. Найти математическое ожидание и сред-

и

нее квадратичное отклонен

е стандартных деталей.

2. Непрерывная

случайная величина

X

имеет плотность рас-

пределения

С

π

< −

;

0 при x

2

π

≤ π ;

f (x) = Acos x при −

≤ x

π

2

2

>

.

0 при x

2

а) найти коэффициент А; б) построить график плотности рас-

пределения f (x);

в)

найти вероятность попадания случайной вели-

чины на интервал

π

;

π

−

4

4

; г) найти функцию распределения F(x) ;