
- •Введение
- •Раздел 1. ЭЛЕМЕНТЫ ТЕОРИИ РЯДОВ
- •§1. Числовые ряды
- •§2. Числовые ряды с неотрицательными членами
- •§3. Знакопеременные и знакочередующиеся ряды
- •§4. Степенные ряды
- •§5. Ряды Фурье для функций с периодом 2π и 2ℓ
- •Вопросы и упражнения для самопроверки
- •Контрольная работа по разделу «Элементы теории рядов»
- •Раздел 2. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТИ
- •§1. Основные правила комбинаторики
- •§3. Операции над событиями
- •§4. Формула полной вероятности. Формула Бейеса
- •§6. Случайные величины. Законы распределения случайных величин. Числовые характеристики
- •§7. Важнейшие примеры распределений
- •Контрольная работа по разделу «Элементы теории вероятности»
- •§1. Задачи математической статистики
- •§2. Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот
- •§3. Эмпирическая функция распределения
- •§4. Числовые характеристики статистического распределения: выборочное среднее, дисперсия
- •§5. Статистическая проверка статистических гипотез
- •§6. Критерий Пирсона для проверки гипотезы о виде закона распределения случайной величины
- •Пример решения контрольной работы
- •Библиографический список
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|||||||
1. Область сходимости: а) 0 ≤ x < 2; |
б) − ∞ < x < +∞ ; в) − 2 ≤ x < 2 ; |
||||||||||||||||||||||||||||
г) − 4 < x < 0 |
; д) − 1 ≤ x < |
1 |
|
. 2. –2 < x < |
|
|
и |
|
< x < 2. |
|
|||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n+1 |
|
|
|
π 2n (x − |
4)2n |
|
|
π (x |
− 4) |
|
|
|
|
|||||||||||||||
∞ |
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
3. ∑(−1) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
|
|
. 4. 0,4992. |
|
||||||||||
|
|
2 42n (2n)! |
|
|
|
|
|
|
|||||||||||||||||||||
n=0 |
|
|
|
|
|
|
|
|
4(2n +1) |
|
|
|
|
||||||||||||||||
5. у(x) = π + |
2π |
(x −1) + |
12π |
(x −1)2 + |
80π |
(x −1)3 + … . |
|
||||||||||||||||||||||
1! |
2! |
3! |
|
||||||||||||||||||||||||||
|
§5. Ряды Фурье для функций с периодом 2π и 2ℓ |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||
|
|
|
|
|
|
|
|
|
|
Теоретический материал |
|
||||||||||||||||||
Рядом Фурье периодической функции |
f (x) с периодом |
2π , оп- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
||||||||
ределенной на сегменте [− π ,π ], называется ряд |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
∞ |
А |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ |
∑(an cosnx + bn sin nx), |
|
||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
π∫ f (x)cos nx dx (n = 0,1,2, ); |
|
|||||||||||||||
|
|
|
|
|
|
a |
n |
|
= |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
π −π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
b |
|
= |
1 |
|
π |
|
f |
(x)sin nx dx (n = 1,2, ). |
|
||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
бπ ∫ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если ряд Фурье сход тся, |
то его сумма S(x) есть периодическая |
||||||||||||||||||||||||||||
функция с периодом 2π , т.е. |
S(х + 2π ) = S(x). |
[− π ,π ] |
|||||||||||||||||||||||||||
Теорема Дирихле. |
Пусть функция |
f (x) на сегменте |
|||||||||||||||||||||||||||
имеет конечноеСчисло экстремумов и является непрерывной за ис- |
|||||||||||||||||||||||||||||
ключением конечного числа точек разрыва 1-го рода (т.е. удовлетво- |
|||||||||||||||||||||||||||||
ряет так называемым условиям Дирихле). Тогда ряд Фурье этой |
|||||||
функции сходится в каждой точке сегмента [− π ,π ] |
и сумма этого |
||||||
ряда S(x) вычисляется: |
|
|
|
||||
1) |
S(x) = f (x) |
во всех |
точках неразрывности |
f (x), лежащих |
|||
внутри сегмента [− π ,π ]; |
|
|
|
||||
2) |
S(x |
) = 1 [f (x |
0 |
− 0)+ f |
(x |
+ 0)], где x − точка разрыва 1-го ро- |
|
|
0 |
2 |
|
0 |
0 |
|
|
да функции |
f (x); |
|
|
|
|
|
|
44
3) |
S |
(x) = 1 [f (− π + 0) |
+ f (π − 0)] на концах промежутка, т.е. при |
||||||||||||||||||||||||
x = ±π . |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае, когда f (x) |
|
– четная функция, ее ряд Фурье содержит |
|||||||||||||||||||||||||
только свободный член и косинусы, т.е. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
f (x) = a0 |
|
|
|
∞ |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
+ |
∑an cosnx, |
|
|
|
||||||||||||||
|
|
|
|
|
2 |
π∫ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n=1 |
|
|
|
|
|
|
|
где an |
= |
|
f (x)cos nx dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
π 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В случае, когда f (x) – нечетная функция, ее ряд содержит толь- |
|||||||||||||||||||||||||||
ко синусы, т.е. |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = |
∑bn sin nx dx, |
|
|
|
|||||||||
|
|
|
|
|
2 |
|
π f (x)sin nxdx. |
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|||||
где b |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n |
|
π |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Часто приходится разлагать в тригонометрический ряд функции |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
– периодическая |
|||
периода, отличного от 2π. В этом случае, если |
f (x) |
||||||||||||||||||||||||||
функция |
с |
периодом |
2 , |
для |
которой |
выполняются на сегменте |
|||||||||||||||||||||
[− , ] |
условия Дирихле, |
то указаннаяДфункция может быть пред- |
|||||||||||||||||||||||||
ставлена в виде суммы ряда Фурье: |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
f (x) = |
|
a |
0 |
|
|
|
∞ Аπ n |
|
|
|
π n |
|
|||||||
|
|
|
|
|
|
|
|
|
|
+ |
∑ |
a |
n |
cos |
|
x + b |
sin |
|
x , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
n=1 |
|
|
|
|
|
n |
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
и |
1 |
|
|
|
|
π n |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
f (x)cos |
x dx; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
an |
= |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
Сb |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
= |
1 |
|
|
f (x)sin π n x dx . |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
||
В случае, когда f (x) – четная функция, ее ряд Фурье содержит |
|||||||||||||||||||||||||||
только свободный член и косинусы, т.е. |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (x) = a0 |
|
|
|
∞ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
∑an cos nπx dx, |
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
f (x)cos nπx dx . |
|
|
2 |
|
|
|
n=1 |
|
|
|
|
|
|
||||||
где a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
= |
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В случае, когда f (x) – нечетная функция, ее ряд Фурье содержит только синусы, т.е.
45

|
|
|
|
|
|
|
∞ |
|
π nx |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = ∑b sin |
|
|
|
|
|
|
|||||
|
= 2 |
f (x)sin π nx dx . |
|
n=1 |
n |
|
|
|
|
|
|
|
|
|
|||
где b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При разложении в ряд Фурье целесообразно придерживаться сле- |
|||||||||||||||||
дующей схемы. Вначале проверяем, что данная функция удовлетво- |
|||||||||||||||||
ряет условиям Дирихле; затем вычисляем коэффициенты |
an |
и bn по |
|||||||||||||||
соответствующим формулам; подставляя их в ряд, получаем искомое |
|||||||||||||||||
разложение; наконец, основываясь на теореме Дирихле, определяем, |
|||||||||||||||||
при каких |
x полученный ряд сходится к данной функции. Рассмот- |
||||||||||||||||
рим примеры разложения в ряд Фурье периодических функций [5]. |
|||||||||||||||||
|
|
|
|
Образцы решения задач |
|
|
|
|
|
|
|||||||
Пример 1. Разложить в ряд Фурье функцию |
f (x) = x |
|
периода 2π, |
||||||||||||||
заданную на интервале −π < х ≤π . |
|
|
И |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
||
-4π |
-4π |
-3π |
|
-2π -π |
0 π |
π |
2π |
3π |
3π |
4π x |
x |
||||||
-3π |
|
-2π |
|
-Аπ 0 |
|
2π |
|
|
4π |
|
|||||||
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Р с. 1.1. График функции f(x)=x |
|
|
|
|
|
||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Эта функция удовлетворяет условиям Дирихле, следо- |
|||||||||||||||||
вательно, может быть разложена в ряд Фурье. Так как функция нечет- |
|||||||||||||||||
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ная, найдем коэффициенты Фурье: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
π |
|
|
|
|
интегрируем по частям |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
b = |
|
|
∫ x sin nx dx = |
x = u, sin nxdx = dv; |
= |
|||||||||
π |
||||||||||||||
n |
|
|
0 |
|
|
|
|
dx = dv, v = − |
1 cos nx |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 |
|
|
|
cos nx |
|
π |
π cos nx |
|
|
|
|||
|
|
|
|
|
|
|||||||||
= |
|
|
− x |
n |
|
|
+ ∫ |
n |
dx = |
|
|
|||
π |
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
46

|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
π |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
− π cos πn |
|
+ 0 cos 0 + |
|
sin n x |
|
= |
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
π |
|
|
|
n |
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
= 2(−1)n+1 . |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= − |
|
2cosπ n |
|
+ |
2sin πn − 2sin 0 |
|
= − 2(−1)n |
|
|
|
||||||||||||||||
|
|
π n |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
πn2 |
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|||||
|
|
|
Следовательно, ряд Фурье функции |
f (x) будет иметь вид |
||||||||||||||||||||||
2 sin x − sin 2x + sin3x − sin 4x + ... + (−1)n sin nx + ... . |
|
|
||||||||||||||||||||||||
|
1 |
|
|
2 |
|
|
3 |
4 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
sin 2x |
|
sin 3x |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin x − |
2 |
|
+ |
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − |
sin 2x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2sin x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Рис. 1.2. Графики функции f(x)=x и её частичных сумм |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
||||
|
|
|
Так как функц я |
f (x) = x |
|
удовлетворяет условиям Дирихле, то в |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
б |
сумма ряда равна значению функ- |
|||||||||||||
любой точке непрерывности |
|
|
f |
(x) |
||||||||||||||||||||||
ции. В точках С‒ nπ ииnπ сумма ряда равна нулю. На рис. 1.2 показаны графики: функции f (x) и частичных сумм ряда, содержащие 1, 2 и 3
члена. Из рисунка видно, как график частичных сумм ряда приближается к графику функции f (x) при увеличении членов суммы.
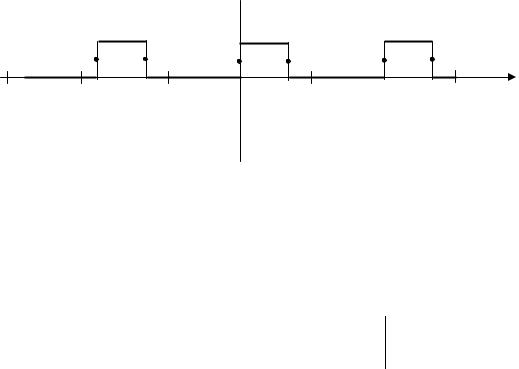
Пример 2. Разложить в ряд Фурье функцию с периодом 2π , заданную на интервале [− π ,π ] формулой
0, − π ≤ x ≤ 0, 2 < x ≤ π; f (x) = 1, 0 < x < 2;
1
, x = 0, x = 2.
2
Решение. Построим график функции (рис. 1.3).
47
 y
y
-3π -2π |
-π |
2 π |
2π |
3π |
x |
Рис. 1.3. График функции
Функция удовлетворяет условиям Дирихле. Находим коэффициенты Фурье
a0 |
= |
1 |
|
∫ f |
(x) dx = 1 ∫ dx = x |
|
2 |
= 2 ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
π |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
π −π |
π 0 |
|
|
|
π |
|
0 |
π |
|
|
|
|
|
2 |
= sin 2n |
− sin 0 = |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
a |
|
|
= |
|
1 π |
f |
(x)cos nx dx = |
1 |
|
21 cos nx dx = |
|
1 |
sin nx |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
n |
|
|
π −∫π |
|
|
|
|
|
|
π 0∫ |
|
|
|
|
|
π n |
И0 |
π n |
π n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
= |
sin 2n |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|||||||||||
|
π n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 π |
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
b |
|
|
= |
|
|
|
|
f |
(x)sin nx dx = |
|
|
|
|
1 |
sin nx dx = − |
|
|
cos nx |
= |
|
|
|||||||||||||
n |
|
|
π −∫π |
|
|
|
|
|
|
π 0∫ |
|
|
|
|
А |
|
π n |
|
|
0 |
|
|
||||||||||||
|
|
|
cos 2n |
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
cos 0 |
1− cosб2n |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= − |
|
π n |
|
− π n = |
|
|
|
π n . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Разложение в ряд Фурье |
f (x) имеет вид |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
f (x) = |
+ |
∑ sin 2n cos nx + 1− cos 2n sin nx . |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
π |
n=1 |
|
|
|
π n |
|
|
|
π n |
|
|
|
|||||||||||
|
|
|
|
Оно справедливо во всей области определения данной функции: в |
||||||||||||||||||||||||||||||
интервале |
(0,2) сумма |
ряда |
S(x) = 1, |
в интервалах |
(−π , 0) и(2,π ) – |
|||||||||||||||||||||||||||||
S(x) = 0 . В точке разрыва x = 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(x) = |
1 |
[f (0 − 0)+ f (0 + 0)]= 1. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
В точке разрыва x = 2,
S(x) = 12 [f (2 − 0)+ f (2 + 0)]= 1.
48
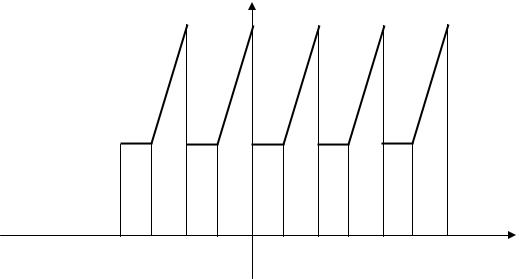
Пример 3. Разложить в ряд Фурье функцию с периодом T = 4 , заданную на интервале(0;4) формулой
( ) 6, 0 < x < 2; f x = 3х, 2 < x < 4.
Решение. Построим график функции (рис. 1.4).
y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
И4 6 8 10 12 |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
-8 -6 -4 -2 0 2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.4. График функции |
|
|
|
|
|||||||||||||||||||
|
|
Эта функция удовлетворяет условиям Дирихле, следовательно, |
||||||||||||||||||||||||||||||||||||||
может быть разложена в ряд Фурье. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Пользуясь формулами |
разложения |
|
в |
ряд |
|
|
Фурье |
|
на сегменте |
|||||||||||||||||||||||||||||
[− , ], |
полагая |
= 2 |
|
|
разб вая интервал интегрирования точкой |
|||||||||||||||||||||||||||||||||||
x = 2 |
на две части, ипоскольку в каждой из них функция задана раз- |
|||||||||||||||||||||||||||||||||||||||
личными формулами, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
an = |
1 |
4 |
|
|
|
|
|
nπx |
|
1 |
|
2 |
|
|
nπx |
|
|
|
4 |
3x cos |
nπx |
dx |
|
= |
|
|||||||||||||||
2 |
∫ |
|
f (x)cosСdx = |
2 |
|
∫6cos |
|
2 |
|
dx +∫ |
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
12 |
|
|
|
nπx |
|
2 |
2π |
|
|
|
nπx |
|
|
|
4 |
|
|
|
|
nπx |
|
4 |
|
|
|
|
6 |
|
|
(1− cos nπ ). |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
|
|
|
sin |
|
|
|
+ 3 |
sin |
|
|
+ |
|
|
|
|
|
|
cos |
|
|
|
|
|
|
= |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
n2π 2 |
|
|
|
|
|
n2π 2 |
|
||||||||||||||||||||||||
|
2 |
nπ |
|
|
|
2 |
|
0 |
nπ |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
При n четном cos nπ =1 и аn |
= 0 , при n нечетном cos nπ = −1 и |
|||||||||||||||||||||||||||||||||||||
an = |
|
12 |
|
, при n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n2 π 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 4 |
|
|
|
|
|
|
1 2 |
|
|
4 |
|
|
|
1 |
|
|
2 3x2 |
|
4 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a0 = |
|
∫ |
f (x)dx = |
∫6 dx +∫3x dx |
= |
|
|
6x |
+ |
|
|
|
|
|
|
=15. |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
0 |
|
|
|
|
|
|
2 0 |
|
|
2 |
|
|
|
|
|
2 |
|
|
0 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
49
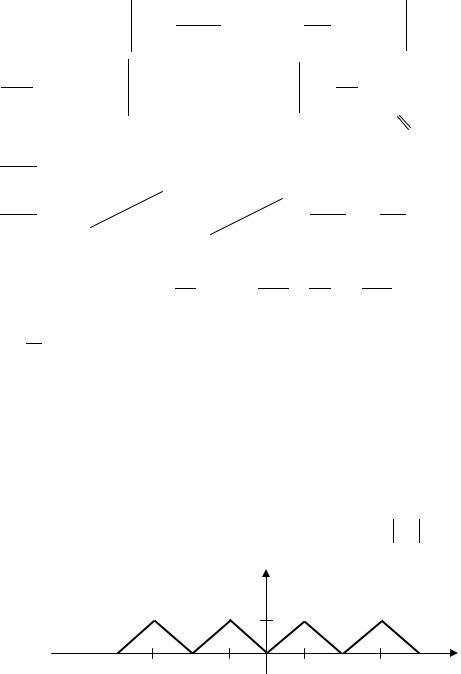
bn = |
1 |
4 |
|
|
|
|
|
nπx |
dx |
= |
1 |
2 |
|
6sin |
|
nπx |
|
|
4 |
|
|
|
|
nπx |
|
= |
||||||||||||||||
2 |
∫ f (x)sin |
|
2 |
|
|
|
2 |
∫ |
|
|
2 |
dx +∫3x sin |
2 |
|
|
dx |
||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||
= |
1 |
|
|
12 |
cos |
nπx |
|
2 |
|
|
|
|
|
|
4 |
|
|
sin |
nπx |
− |
2x |
cos |
nπx |
4 |
|
= |
|
|||||||||||||||
2 |
− |
nπ |
|
2 |
|
|
|
|
+ 3 |
|
|
|
|
|
|
|
2 |
nπ |
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
n2π 2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||
= |
|
1 |
|
12cos |
|
πnx |
0 |
+ |
3 |
|
2x |
− cos |
πnx |
4 |
4 |
2 |
cos |
πnx |
|
|
= |
|||||||||||||||||||||
2πn |
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
+ ∫ |
πn |
|
2 |
|
dx |
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
πn |
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
= |
|
|
[12(1 − cos nπ )− 3(2 4cos2πn − 4cos πn)]= |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
1 |
|
[12 −12cos nπ + 24 +12cosnπ ]= |
−12 |
= − |
|
6 . |
|
|
|
|
||||||||||||||||||||||||||||||
|
2nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2nπ |
|
|
nπ |
|
|
|
|
|||||
|
Искомое разложение данной функции имеет вид |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
f (x) = |
15 |
+ |
|
12 |
|
|
|
πx |
+ |
|
1 |
cos |
3πx |
+ |
1 |
cos |
5πx |
|
|
|
|
|
||||||||||||||||||
|
|
2 |
π 2 |
|
cos |
|
2 |
|
9 |
2 |
25 |
2 |
|
+ ... − |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
− |
6 |
|
πx |
+ |
1 |
sin |
2πx |
+ |
1 |
sin |
|
3πx |
|
|
|
|
И |
|
|||||||||||||||||||||||
|
|
sin |
2 |
2 |
|
2 |
|
|
3 |
|
2 |
+ ... . |
|
|||||||||||||||||||||||||||||
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Оно справедливо во всей области определения данной функции: в |
|||||||||||||||||||||||||||||||||||||||||
интервале (0,2) сумма ряда S(x) = 6 ,Дв интервале (2,4) – S(x) = 3x . В |
||||||||||||||||||||||||||||||||||||||||||
точке разрыва x = 2, |
|
|
|
|
|
|
|
|
1 |
А |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (2 + 0)]= 6. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(x) = |
2 |
[f |
(2 − 0) + |
|
||||||||||||||||||||
|
|
Пример 4. |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Разлож ть в ряд Фурье функцию с периодом T = 2 , |
||||||||||||||||||||||||||||||||||||||||
заданную на интервале |
(−1,1) формулой f (x) = |
|
x |
|
|
(рис. 1.5). |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
-4 -3 -2 -1 0 |
|
|
1 2 |
|
3 |
|
|
4 x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.5. График функции |
|
||||||||||||||
Решение. Функция удовлетворяет условиям Дирихле. Функция f (x) – четная; полагая =1, получим
|
1 |
x2 |
|
|
1 |
|
|
|
|
||||
a0 |
= 2∫ x dx = 2 |
|
|
|
|
=1; |
2 |
|
|
0 |
|||
|
0 |
|
|
|
50
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
sin nπx + |
|
|
|
|
|
= |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|||||||||
an = 2∫ x cos nπx dx = 2 |
|
|
|
|
cos nπx |
|
|
||||||||||||||||
|
0 |
|
|
|
|
|
nπ |
|
|
|
|
n |
|
π |
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
0, |
n − четные; |
|
|
|
|
|
|
|
||||||||
= |
|
(cos nπ −1) = |
|
|
4 |
|
, |
n − нечетные. |
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
n2 π 2 |
|
|
|
|
− |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n |
2 |
π |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
(x) = |
1 |
− |
4 |
∞ cos(2n −1)πx |
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
∑ |
(2n −1)2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
π 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задачи для самостоятельной работы
1. Разложить в ряд Фурье функцию с периодом 2π , заданную на
интервале [− π ,π |
] уравнением f (x) |
|
|
|
− 2x |
при |
− π ≤ x < 0; |
|||||||
|
= |
3x |
при |
0 ≤ x ≤ π. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Д |
2π , заданную на |
|||
2. Разложить в ряд Фурье функцию с периодом |
||||||||||||||
интервале [0, 2π ] формулой f (x) = |
x |
. |
|
И |
|
|||||||||
2 |
|
|||||||||||||
|
|
|
|
|
А |
|
|
|
||||||
3. Разложить в ряд Фурье функцию с периодом 2π , заданную на |
||||||||||||||
интервале [− π ,π |
] формулой |
y = |
sin x |
. |
|
|
|
|||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
||
4. Разложить в ряд Фурье периодическую функцию f (x) с перио- |
||||||||||||||
|
|
|
и |
|
|
|
,π ] уравнением |
f (x) = π + x . |
||||||
дом 2π , заданную на интервале [− π |
||||||||||||||
5. Разложить в ряд Фурье периодическую функцию |
||||||||||||||
x |
при |
0 ≤ x < 1; |
|
|
f(x+2)=f(x) |
|
||||||||
f (x) = |
|
|
|
1 ≤ x ≤ 2. |
|
|
|
|||||||
2 − x при |
|
|
|
|
|
|
|
|||||||
6. Разложить в ряд Фурье периодическую функцию |
||||||||||||||
|
0 |
при |
− 3 < x ≤ 0; |
|
|
f(x+6)=f(x) |
|
|||||||
f (x) = |
|
С |
0 < x < 3. |
|
|
|
|
|||||||
x |
|
при |
|
|
|
|
|
|
|
|||||
7. Разложить в ряд Фурье периодическую функцию |
||||||||||||||
f (x) = 10 − x |
при 5 < x < 15, |
|
|
f (x +10) = f (x). |
||||||||||
Ответы
1.f (x)
2.f (x)
= |
5π |
− |
10 |
cos |
x |
+ |
cos 3x |
+ |
cos 5x |
|
sin x |
− |
sin 2x |
|
||
4 |
π |
|
12 |
|
32 |
52 |
+ ... |
+ |
1 |
2 |
+ ... . |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
=π − ∑∞ sin nx . 2 n=1 n
51
