Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1802.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.85 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

χ2 = 0,0,532209 + 0,1,542116 + 1,4,112321 + 8,973,88 + 014,66,4356 + 18,999,06 + 19,645,56 +

+015,21,0441 + 9,542,37 + 4,486,15 + 01,71,3741 + 0,0,482704 = 4,5.

Согласно теореме Пирсона, при n → ∞ распределение величины

χ 2 зависит от параметра k , который называют числом степеней сво-

боды. k = l – 1 – r, где r – число параметров предполагаемого распределения, оцененных по данным выборки; l – число интервалов. Число степеней свободы k = 8 −1− 2 = 5 . Выберем уровень значимости

α = 0,05 и по таблице квантилей χ 2 -распределения для числа степеней свободы k = 5 и уровня значимости α = 0,05 (см. прил. 4) найдем

1.Что такое вариационныйбряд?АДИ

2.Дать определен ие эмп р ческой функции распределения и числовых характеристик выборки.

3.СформулируйтеСсвойства оценок.

4.Как определяется довер тельный интервал для оценки математического ожидания?

5.Дайте определение статистической гипотезы.

6.Дайте понятие критерия согласия.

7.Сформулируйте основные этапы проверки статистической гипотезы о законе распределения случайной величины. :

Пример решения контрольной работы

Задача

а) ∑∞ 7n

n=12n

1. Исследовать сходимость следующих числовых рядов.
+1	; б)	∞ n +1		n	∞ ln(n +1)+1		.
+1		∑	2		; в) ∑	(n +1)
		n=1			n=1

139

Решение

а) Используем признак Даламбера для исследования на сходи-

мость данного ряда:

7n+1 +1

an+1

2n +

an+1

7n+1

2 + n

Тогда

lim

= 7 >

2n + 3

n→∞

2 + n

1 +

Ряд расходится, так как предел больше 1.

б) Используем предельный признак Коши для

исследования на

сходимость данного ряда: an

n +1 n

n +1

Тогда

lim n

= lim n

= ∞.

n→∞

Ряд расходится, так как предел больше И1.

в) Используем интегральный признак для исследования на схо-

димость данного ряда.

Подынтегральная функция непрерывна на промежутке [1;∞).

∞ ln(x +1)+1

t = ln(x +

1)+1

∞

(ln(x +1)+1)

∫

dx =

∫ tdt = lim

= lim

(x +1)

b→∞

x +

lim (ln((b +1)+1)

− (ln 2 +1) )= ∞.

2 b→∞

Ряд расходится, так как несобственный интеграл, соответствую-

щий данному рядуС, стремится к бесконечности, т.е. расходится.

Задача 2. Исследовать сходимость следующих степенных рядов.

Найти их области сходимости.

∞ xn

;б)

∞ (x + 3)n

а) ∑

∑

n=1 n!

n=1

Решение

а) Найдем радиус сходимости ряда

R = lim

;

; a

an+1

n+1

(n +1)!

n→∞

140

Тогда

(n +1)!= lim

(n +1) = ∞ .

R = lim

= lim

an+1

n→∞

n→∞ n!

n→∞

Ряд сходится при x (− ∞;∞).

б) Найдем радиус сходимости ряда

R = lim

; an =

; an+1 =

an+1

3n+1

n→∞

Тогда

3n+1 = 3.

R = lim

= lim

an+1

n→∞

n→∞ 3n

Следовательно, ряд сходится для значений х, удовлетворяющих

неравенству

x + 3

< 3, или − 6 < x < 0 .

Исследуем сходимость ряда на концах промежутка.

При x = −6 получим ряд

∞

который расходится, так как

∑ (−1)n ,

n=1

последовательность частичных сумм этого ряда не имеет предела.

∞

При x = 0 получим ряд ∑1n = 1+Д1+1+ ... +1+ ..., который расхо-

n=1

дится согласно необходимому признаку сходимости рядов (n-й член

ряда не стремится к нулю).

Следовательно, промежутком сходимости ряда является интервал

(− 6;0).

Задача 3. Вычислить определенный интеграл с помощью разложения подынтегральной функции в степенной ряд. Обеспечить абсолютную погрешность h < 0,001:

1	2	x		2
				dx .
∫ cos
			5
0

Решение

12	x		2
Соответствующий неопределенный интеграл ∫ cos			dx не
Соответствующий неопределенный интеграл ∫ cos		5	dx не
0		5

может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона−Лейбница здесь нельзя. Вычислим интеграл приближенно.

141

Разложим подынтегральную функцию в степенной ряд

cos x = 1

−

+ ...

(−1)n x2n

...,

x (−∞;+∞);

(2n)!

x 2

2 4

(−1)

cos

=1−

−

+ ...+

+ ...,

(2n)!

x (−∞;+∞);

(−1)

cos

=1−

−

+ ... +

+ ...,

(2n)!

x (−∞;+∞);

(x)4

(x)8

(x)12

(−1)n (x)4n

cos

= 1 −

−

+ ... +

...,

512 6!

54nИ(2n)!

x (−∞;+∞). Д

Интегрируя этот ряд почленно (это возможно, так как пределы

интегрирования принадлежат интервалу сходимости данного ряда),
получаем									2														А
1		2	cos				x		2				1		2					x	4						x	8				x	12		(−1)			n	x	4n
		2													2						4							8					12					n		4n
									dx =							1 −								+						−				+ ... +							+ ... dx =
	∫								dx =					∫		1 −								+						−				+ ... +							+ ... dx =
	∫													∫				б									8				12					4n
0						5												5		4		2! 5					8				12			5		4n	(2n)!
0						5							0					5				2! 5							4! 5				6!	5			(2n)!
										5		1	2						9				1		2
												1											1

				1					x					и
	= x				2 −				x						+			x								+ ...
	= x			0	2 −			55			2!	0			+		9	58 4!					0			+ ...
				0				55			2!	0					9	58 4!					0
	Так как полученныйС																			ряд удовлетворяет условиям Лейбница и
1						< 0,001, достаточно взять первый член, чтобы получить ис-
	25 55 2!					< 0,001, достаточно взять первый член, чтобы получить ис-

комое значение с заданной точностью. Таким образом, находим

12 cos x 2 dx ≈ x 1 = 0,5.

∫ 5 02 0

Задача 4. В группе из восьми студентов шесть мастеров спорта. Найти вероятность того, что из двух случайным образом отобранных

142

спортсменов хотя бы один – мастер спорта. В ответ записать число, имеющее три знака после запятой без округления.

Решение

Обозначим событие А ={из восьми спортсменов хотя бы один – мастер спорта}.

Найдем вероятность события А, применив формулу классической вероятности.

P(A) = mn .

Общее число n исходов испытания равно числу сочетаний из восьми по 2 и составляет n = C82 .

Событие A и событие А ={из двух отобранных спортсменов нет ни одного мастера спорта} составляют полную группу, тогда вероятность P(A) равна

			C0	1
			C0	1
			Д
P(A) =1	− P(A) =1−		6 =1−	28	= 0,964.
			C2	28
			8
		А
Задача 5. Для поисков спускаемого аппаратаИкосмического ко-
рабля выделено 4 вертолета первого типа и 6 вертолетов второго ти-
	б

па. Каждый вертолет первого типа обнаруживает находящийся в районе поиска аппарат с вероятностью 0,6, второго типа – с вероятно-

стью 0,7. а) Найти вероятностьи того, что наугад выбранный вертолет

обнаружит аппарат. б) Вертолет обнаружил спускаемый аппарат. Найти вероятность того, что он принадлежит к первому типу. В ответ записать суммуСполученных ч сел, записанных с двумя знаками после запятой без округления.

Решение

A={вертолет обнаружит аппарат}. Возможны гипотезы: Н1={вертолет первого типа}; Н2={вертолет второго типа}.

P(H1) = 0,4; P(H2 ) = 0,6.

Найдем условные вероятности

P(A/ H1) = 0,6; P(A/ H2 ) = 0,7.

а) Используем формулу полной вероятности

P(A) = ∑ P(Hi ) P(A/ Hi ) ;

i=1

P(A) = 0,4 0,6 + 0,6 0,7 = 0,66.

143

б) Используем формулу Байеса

P(Hi / A) =	P(Hi )P(A / Hi )			.
P(Hi / A) =	2			.
	∑ P(Hi ) P(A / Hi )
Тогда	i=1
Тогда
P(H1 / A) = P(H1)P(A/ H1)		= 0,24	= 0,36.
	P(A)	0,66

Ответ: 1,02.

Задача 6. Размеры диаметров деталей, выпускаемых цехом, – случайная величина, распределена по нормальному закону; М[X]= =5 см; D[X]=0,81cм2. Найти вероятность того, что диаметр наугад взятой детали – от 4 до 7 см. Ответ записать с тремя знаками после запятой без округления, учитывая, что Ф(1,11) = 0,3665; Ф(1) = 0,3413;

Ф(1,15) =0,3749; Ф(2,22) =0,4868.

σД

Решение

Вероятность попадания значений нормальной случайной величи-

ны в интервал (α,β ) определяется формулойИ

P(α ≤ X

≤ β ) =

β − a

α − a

− Ф

По условию,

a = 5;

σ =

D(X )

= 0,9;

α = 4; β = 7 , тогда

7 − 5

4 − 5

P(4

≤ X ≤ 7) = Ф

0,9

−Ф

0,9

= Ф(2,22)−Ф(−1,11)=

= Ф(2,22)+ Ф(1,11)= 0,4868 + 0,3665 = 0,8533.

Задача 7. Наблюдения за межремонтными интервалами Т (в месяцах) работы зерноуборочного комплекса дали результаты, приведенные ниже:

0,000; 0,000 0,002 0,006 0,023 0,084 0,382 0,810 0,003 0,864 1,033 0,912 0,093 0,323 0,194 0,522 2,336 0,057 0,648 0,250 0,877 0,271 0,037 0,537 0,183 1,306 0,752 0,198 1,623 0,875 0,184 0,276 0,613 0,362 0,654 0,676 1,079 0,500 0,900 0,191 0,250 0,348 0,318 0,182 0,458 0,936 0,567 0,303 0,487 0,522

1.Составить выборочное распределение.

2. Построить гистограмму и график выборочной функции распределения.

144

3.Найти состоятельные несмещенные оценки математического ожидания и дисперсии.

4.Построить доверительные интервалы для математического ожидания и дисперсии с уровнем доверия р = 0,95.

5.На основании анализа формы построенной гистограммы выдвинуть гипотезу о законе распределения и проверить справедливость гипотезы по критерию Пирсона с уровнем значимости α=0,05.

Решение

1. Первым этапом статистического изучения вариации являют-

ся построение вариационного ряда [упорядоченного распределения единиц совокупности по возрастающим (чаще) или по убывающим (реже) значениям признака] и подсчет числа единиц с тем или иным

значением признака. Для этого сначала построим ранжированный
	И
ряд. Ранжированный ряд – это перечень отдельных единиц совокуп-
ности в порядке возрастания (убывания) изучаемого признака.
Построим ранжированный ряд:	Д

0,000 0,000 0,002 0,003 0,006 0,023 0,037 0,057 0,084 0,093
0,182 0,183 0,184 0,191 0,194 0,198 0,250 0,250 0,271 0,276
0,303 0,318 0,323 0,348 0,362 0,382 0,458 0,487 0,500 0,522
0,522 0,537 0,567 0,613 0,648 0,654 0,676 0,752 0,810 0,864
		б
0,875 0,877 0,900 0,912 0,936 1,033 1,079 1,306 1,623 2,336
1. Находим размах вы орки
	и
	R = xmax − xmin =А2,336 − 0,000 = 2,336 .
2. Назначаем ч сло част чных интервалов к.
	С			к=10. Находим длину (шаг разбие-
Обычноk = 9 ÷12. Выберем
ния):			R =	2,336
		∆ =			≈ 0,24.
				10
			k

3) Численность отдельной группы сгруппированного ряда опытных данных называется выборочной частотой. Обозначается: ni – вы-

борочная частота.

∑k ni* = n.

i=1

Относительная выборочная частота – отношение выборочной частоты данных вариантов к объёму выборки. Обозначается: pi* – относительная выборочная частота.

145

pi* = ni , n

где i – номер варианты.

Выборочная относительная частота сходится по вероятности к соответствующей вероятности.

∑k pi* =1.

i=1

2. Построение гистограммы плотностей относительных частот.

							∆		Таблица 24
							∆	2
i	[аi ; ai +1]	n i				hi* =	pi*		~xi =	xi + xi+1
							pi*

1	0-0,24	16		0,32		1,333			0,12
					И
2	0,24-0,48	11		0,22		0,917			0,36

3	0,48-0,72	10		0,2		0,833			0,6
				Д
4	0,72-0,96	8		0,16		0,667			0,84
5	0,96-1,2	2		0,04		0,167			1,08
			А
6	1,2-1,44	1		0,02		0,083			1,32
7	1,44-1,68	1		0,02		0,083			1,56
8	1,68-1,92	0		0		0			1,8

9	1,92-2,16	и		0		0			2,04
9	1,92-2,16	0		0		0			2,04
10	2,16-2,4	1		0,02		0,083			2,28
		б
		∑=50		∑=1

ных интервалов;*С– определяет эмпирические значения.

Примечание. hi* − плотность относительной частоты; xi − середина частич-

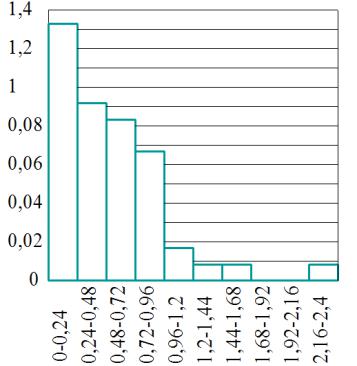
Построим гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной ∆ = 0,24 , а высоты равны отношению

h* =	p*
	i	. Площадь всей гистограммы должна быть равна 1. Гисто-
		. Площадь всей гистограммы должна быть равна 1. Гисто-
i	∆

грамма является оценкой генеральной функции плотности f(x). Полученные значения высот вносим в табл. 24.

Строим гистограмму относительных частот.

146

Рис. 3.8. Гистограмма относительных частот

можно выдвинуть гипотезу о по-

По виду гистограммы (рис. 3.8)

казательном законе распределенияАслучайной величины X.

25,92

∑ xi ni

а ≈ xв =

i=1

= 0,52;

С l

− x

)

∑(x

σ 2 ≈ D

i=1

= 9,17 = 0,18,

т.е.

= 0,18.

∑n

− (xв )

n i=1

147

		Таблица 25

2,56	1,92
0,28	3,96
0,06	6
0,82	6,72
0,63	2,16
0,64	1,32
1,08	1,56
0	0
0	0
3,1	2,28
	∑=25,92

s= 0,43(табл.С25). ибАДИ

4.Построим довер тельные интервалы для математического ожидания и дисперсии. Найдем доверительный интервал для оценки с на-

дежностью 0,95 неизвестного математического ожидания M(Х) показательно распределенного признака X генеральной совокупности, ес-ли генеральное стандартное отклонение s = 0,43, отклонениевыборочная сред-

няя хв = 0,52, объем выборки n = 50. Требуется найти доверительный интервал

х − t

; х + t

Все величины, кроме tγ , известны. Найдем tγ из соотношения

Ф(t)= γ2 = 0,295 = 0,475.

148

По прил. 2 находим tγ= 1,96.

Подставив tγ= 1,96;

х = 0,52; s = 0,43;n = 50 , окончательно полу-

чим доверительный интервал для М(х):

х − t

; х + t

I p = (0,4;0,64).

Найдем доверительный интервал для оценки дисперсии D(х).

Согласно формуле (3.7)

(n −1)s2

≤ σ

≤

(n −1)s

, а так как при

χ22

χ12

k=50–1=49 верхняя доверительная граница равна

χ22 (р;к) =

1−γ

(0,05;49) = 67,5,

χ22

;

к = χ22

нижняя определяется как

1−γ

χ 2 (р;к) = χ 2

χ 2 (0,95;49) = 34,8

−

;к

(см. прил. 4),

то

49 0,432

≤ σ ≤

0,432

67,5

34,8

или 0,3663 ≤ σ ≤ 0,51 – эта оценка не

симметрична относительно σ.

5. Построенная гистограмма по форме напоминает график плот-

ности вероятности показательного распределения. Поэтому естест-

венно выдвинуть г потезу о показательном распределении случайной
		С
величины Х. Провер м справедливость выдвинутой гипотезы по кри-
терию Пирсона с уровнем значимости α=0,05.
				f (x)= λ e−λx ;
				λ =	1 =		1	=1,92;
				λ =	1 =	0,52		=1,92;
					x	0,52
				f (x)=1,92 e−1,92x .
	Найдем вероятности попадания Х в каждый из интервалов по
формуле
P = P(x < X < x			) = e−λxi − e−λxi+1 .
i	i	i+1
P	= P(0 < X < 0,24)= e0 − e−1,92 0,24 =1− 0,631 = 0,369;
1	= P(0,24	< X < 0,48)= e−1,92 0,24				− e−1,92 0,48 = 0,631− 0,398 = 0,233;
P	= P(0,24	< X < 0,48)= e−1,92 0,24				− e−1,92 0,48 = 0,631− 0,398 = 0,233;
2		< X < 0,72)= e−1,92 0,48
P	= P(0,48	< X < 0,72)= e−1,92 0,48				− e−1,92 0,72 = 0,398 − 0,251 = 0,147;
3
P = P(0,72		< X < 0,96)= e−1,92 0,72				− e−1,92 0,96 = 0,251− 0,158 = 0,093;
4

149

P5 = P(0,96 < X <1,2)= e−1,92 0,96 − e−1,92 1,2 = 0,158 − 0,1 = 0,058; P6 = P(1,2 < X <1,44)= e−1,92 1,2 − e−1,92 1,44 = 0,1− 0,063 = 0,037; P7 = P(1,44 < X <1,68)= e−1,92 1,44 − e−1,92 1,68 = 0,063 − 0,4 = 0,023;

P = P(1,68 < X <1,92)= e−1,92 1,68 − e−1,92 1,92					= 0,4 − 0,25 = 0,015;
8
P = P(1,92 < X < 2,16)= e−1,92 1,92 − e−1,92 2,16					= 0,25 − 0,16 = 0,009;
9	= P(2,16 < X < 2,4)= e−1,92 2,16 − e−1,92 2,4
P	= P(2,16 < X < 2,4)= e−1,92 2,16 − e−1,92 2,4				= 0,16 − 0,01 = 0,006;
10	= P(2,4 < X < ∞)= e−1,92 2,4 − e−∞ = 0,01− 0 = 0,01.
P	= P(2,4 < X < ∞)= e−1,92 2,4 − e−∞ = 0,01− 0 = 0,01.
∞	Найдем теоретические частоты:
	Найдем теоретические частоты:
	n1′	= n P1 = 50 0,369 =18,45;
	′	= n P2 = 50 0,233 =11,65;
	n2	= n P2 = 50 0,233 =11,65;
	′		= n P3 = 50 0,147 = 7,35;
	n3		= n P3 = 50 0,147 = 7,35;
	′				И
	n4		= n P4 = 50 0,093 = 4,65;
	′		= n P5 = 50 0,058 = 2,9;
	n5		= n P5 = 50 0,058 = 2,9;
	′			Д
	n6		= n P6 = 50 0,037 =1,85;
	′		= n P7 = 50	0,023 =1,15;
	n7		= n P7 = 50	0,023 =1,15;
	′		А
	n8		= n P8 = 50 0,015 = 0,75;
	′		= n P9 = 50 0,009		= 0,45;
	n9		= n P9 = 50 0,009		= 0,45;
	′		б
	n10		= n P10 = 50 0,006 = 0,3;

n∞′ = n P∞ = 50 0,01 = 0,5.

Сравним эмп р ческ е теоретические частоты с помощью критерия Пирсона. Для этого cоставим расчетную таблицу, причем объе-

диним малочисленные частоты и сответствующие им теоретические
частоты.				и
			С							Таблица 26
	i			′		′		′			′

	1	16		18,45	-2,45		6,0025		0,3752
	2	11		11,65	-0,65		0,4225		0,0384
	3	10		7,35	2,65		7,0225		0,7023
	4	8		4,65	3,35		11,225		1,4028
	5	2		2,9	-0,9		0,81		0,405
	6	2		0,75	1,25		1,5625		0,7812
	7	1		0,25	0,75		0,5625		0,5625
									χ2набл = 4,2674

150

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1816 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.84 Mб81799.pdf
#
07.01.2021201.85 Кб018.pdf
#
07.01.2021329.58 Кб0180.pdf
#
07.01.20211.84 Mб21800.pdf
#
07.01.20211.84 Mб01801.pdf
#
07.01.20211.85 Mб171802.pdf
#
07.01.20211.85 Mб21803.pdf
#
07.01.20211.85 Mб111804.pdf
#
07.01.20211.86 Mб21805.pdf
#
07.01.20211.86 Mб21806.pdf
#
07.01.20211.86 Mб31807.pdf