Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1802.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.85 Mб

Скачать

☆

1 / 181 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Министерство образования и науки Федеральное бюджетное образовательное учреждение высшего образования «Сибирская государственная

автомобильно-дорожная академия (СибАДИ)»

Кафедра «Высшая математика»

Е.Ю. Руппель

		И
МАТЕМАТ КА:
	Д
ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ.
А
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
б
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
С
иУчебное пособие

Омск ♦ 2016

Согласно 436-ФЗ от 29.12.2010 «О защите детей от информации, причиняющей вред их здоровью и развитию» данная продукция

УДК 512 маркировке не подлежит.

ББК 22.14 Р86

Рецензенты:

канд. физ.- мат. наук, доц. Ю.Б. Никитин (ФГБОУ ВПО ОмГМУ); канд. техн. наук, доц. А.С. Котюргина (ФГБОУ ВПО ОмГТУ)

Работа утверждена редакционно-издательским советом СибАДИ в качестве учебного пособия.

Руппель, Елена Юрьевна.

Р86 Математика: Числовые и функциональные ряды. Элементы теории вероят-

ностей и математической статистики [Электронный ресурс] : учебное пособие/ Е.Ю.

Руппель. –Электрон. дан. − Омск : СибАДИ, 2016. – URL: http://bek.sibadi.org/cgi-bin/ irbis64r_plus/cgiirbisСибАДИ64 ft.exe. - Режим доступа: для авторизованных пользователей.

ISBN 978-5-93204-951-8.

Является руководством к решению задач по разделам математики «Числовые и функциональные ряды», «Элементы теории вероятностей и математической статистики» для студентов заочной формы обучения. Ко всем разделам приведены необходимые теоретические пояснения, детально разобраны типовые задачи. В каждом разделе содержатся задания для самостоятельной работы студентов, приведены вопросы для

самопроверки и контрольная работа.

Имеет интерактивное оглавление в виде закладок. Содержит видеофрагмент обучающего характера длительностью 1 час 36 минут, который воспроизводится по интерактивной ссылке с помощью про грывателя Windows Media.

Предназначено для обучающ хся по техническим направлениям, преподавателей и аспирантов, изучающ х курс математики.

Мультимедийное издание (2,0 МБ)

Системные требования : Intel, 3,4 GHz ; 150 МБ ; Windows XP/Vista/7 ; DVD-ROM ;

1 ГБ свободного места на жестком диске ; программа для чтения pdf-файлов

Adobe Acrobat Reader; Google Chrome ; Windows Media Player, колонки

Редактор И.Г. Кузнецова Техническая подготовка − Т.И. Кукина

Издание первое. Дата подписания к использованию 05.10.2016

Издательско-полиграфический центр СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПЦ СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1

«Высшее назначение математики … состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает».

Н. Винер

Введение

В пособии представлены материалы, необходимые для изучения таких разделов курса «Высшая математика», как «Теория рядов» и «Теория вероятностей и математическая статистика» студентами технических направлений высших учебных заведений. Пособие не содержит подробного теоретического материала, т.е. не дублирует известных учебников по данным дисциплинам. Основная особенность пособия ‒ сочетание необходимого теоретического материала с широким использованием методов решения основных типов задач по из-

него чтения лекций для студентов техническихИнаправлений и переработки уже известной литературы по данным разделам. Опыт работы в вузе выявил особенности в изложении теоретического материала

ложенным в нём разделам курса.

для студентов технических направленийД. Основной принцип ‒ его доступность в сочетании со строгостью изложения, поэтому пособие

Идея написания такого пособия пришла автору после многолет-

отличается высоким уровнем строгостиАи методической продуманности изложенных тем, точностью формулировок основных понятий и

теорем, краткостью идоступностьюб при решении задач. Предложенные для решенияСзадачи прошли многолетнюю апробацию. Пособие содержит задачи по всем разделам теории вероятностей и теории рядов, изучаемых в технических вузах. Большинство задач сопровождаются решениями, а те из них, которые предлагаются для самостоятельного решения, ‒ ответами. В учебном пособии приведен подробный разбор типовых задач по теории вероятностей и математической статистике, решение которых позволит студенту глубже понять тео- ретико-вероятностные построения, научиться применять их при проведении конкретных экспериментов и опытов в своей инженерной и экспериментальной деятельности. Пособие содержит необходимые для решения задач таблицы и соответствует требованиям, предъявляемым к компетенциям Федерального государственного образовательного стандарта высшего образования.

Раздел 1. ЭЛЕМЕНТЫ ТЕОРИИ РЯДОВ

§1. Числовые ряды

Теоретический материал

Определение 1. Числовой ряд есть алгебраическая сумма бесконечного числа слагаемых. Всякий ряд имеет, таким образом, вид

a1 + a2 + a3 + + an−1 + an + an+1 + .

Причем написанное выражение не имеет последнего члена, но за каждым из слагаемых имеется следующее слагаемое.

Для сокращенного обозначения рядов используется знак сумми-

рования Σ, а именно:	И
a1 + a2	∞
a1 + a2	+ + an + = ∑an .
	n=1

Определение 2. Числа a1 , a2 ,..., an ,... называются членами ряда

∞

∑ an , an называется общим членом ряда.

n=1

Рассмотрим некоторые примеры рядов. В курсе математики

средней школы мы уже встречались Дс понятием ряда, который полу-

чается при вычислении суммы членов геометрической прогрессии:

Аn

∞

a + aq + + aq

+ =

∑ aq

б∞

n=0

Определение 3. Ряд

∑ aqn

называется рядом геометрической

n=0

прогрессии.

Если, например, a = 1; q =

, то получим ряд

∞

∑

n=0 5

Определение 4. Ряд

∞

= 1+

+ +

∑

n=1n

называется гармоническим рядом.

Определение 5. Сумма первых n членов ряда называется час-

тичной суммой ряда.

Если частные суммы ряда становятся все более и более точными

приближениями некоторого числа, то ряд мы назовем сходящимся, т. е. если существует число S , для которого S1, S2 ,..., Sn ,... являются приближенными значениями, то S называют суммой ряда и пишут

a1 + a2 + a3 + + an + = S .

∞

Определение 6. Ряд ∑ an называется сходящимся, если последо-

n=1

вательность его частных сумм S1, S2 ,..., Sn ,... сходится, т.е. если существует конечный предел

nlim→∞ Sn = S .

Если lim Sn				не существует или lim Sn = ∞,							то ряд называется
n→∞									n→∞
расходящимся			и	ему		не приписывается никакое числовое значе-
ние[1].										И
Свойства сходящихся рядов:									Д
Свойства сходящихся рядов:
				∞				А
1. Если ряд				∑ an		сходится и его сумма равна S , то для прои з-
			n=1				б
вольного числа c ряд
					∞		= ca1 + ca2		+ + can +
					∑ can		= ca1 + ca2		+ + can +
					nи
				n=1
также сходится и его сумма равна cS . Если же ряд											∞
также сходится и его сумма равна cS . Если же ряд											∑ an расходится и
		С									n=1
c ≠ 0 , то и ряд			∞
c ≠ 0 , то и ряд			∑ ca расходится.
			n=1
2. Если ряды
∞	= a1 + a2 + + an + и								∞
∑ an	= a1 + a2 + + an + и								∑ bn = b1 + b2 + + bn +
n=1									n=1
сходятся и их суммы равны соответственно S ′ и S ′′, то и каждый из
двух рядов
∞			± bn )= (a1 ± b1 )+ (a2						± b2 )+ + (an ± bn )+
∑ (an			± bn )= (a1 ± b1 )+ (a2						± b2 )+ + (an ± bn )+
n=1

сходится и сумма каждого равна соответственно S ′ ± S ′′.

Другими словами: сходящиеся ряды можно почленно складывать и вычитать.

∞

3. Если в ряде ∑ an добавить или отбросить конечное число чле-

n=1

нов, то полученный ряд

a1′ + a2′ + + an′ +

сходится или расходится одновременно с данным. В случае сходимости рассматриваемых рядов их суммы отличаются на сумму добавленных или отброшенных членов.

∞

4. Если ряд ∑ an сходится, то его общий член an стремится к ну-

n=1

лю.

Следствие. Если n-й член стремится к нулю, еще не следует, что ряд сходится, ряд может и расходиться.

Образцы решения задач

Пример 1. Исследуем на сходимость ряд геометрической

грессии

∞

∑ aqn .

n=0

nД+1

Решение

n+1

Sn = a + aq + aq2

+ + aqn = a(1 − q

)

= a − aq

− aq

1− q

1 − q

1− q

Рассмотрим q , удовлетворяющее условию

< 1.

Тогда

aqn+1

S = lim S

= lim

−

= lim

− lim

n→∞

n→∞ 1− q n→∞

1− q

n→∞

1− q

−

lim qn+1

−

1 − q

1 − q nС→∞

про-

∞

Итак, при

< 1 ряд

∑ aqn сходится и его сумма S равна

. В

1 − q

n=0

частности, сумма ряда

∞

равна

S =

∑

n=0

1 −

∞

Если

≥ 1,

то ряд

∑ aqn сходится лишь при a = 0 . В этом слу-

n=0

чае Sn = 0 и, следовательно,

lim Sn

= 0. Если

a ≠ 0 и

≥ 1, то

n→∞

lim Sn

= lim

a(1 − qn+1 )=

lim(1

− qn+1 )=

∞ = ∞ , т.е. ряд

1 − q

n→∞

1 − q

1 − q n→∞

∞

расходится.

∑ aqn

n=0

Если a ≠ 0 и

= 1, то получим при q = 1 ряд

а + а + + а + .

Следовательно, lim

Sn = lim n a = a lim n = a ∞ = ∞ , т.е. ряд

n→∞

является расходящимся. При q = −1 ряд

a − a + a − a + + (−1)n+1a + ,

где S2n = 0; S2n−1 = a , следовательно, последовательность частичных сумм a , 0, a , 0,... не имеет предела.

Пример 2. Исследовать на сходимость ряд

ln 2 + ln 3 + ln 4 + ln 5 + + ln n + 1 +

= ∑ ln n + 1 .

∞

n=1 n

Решение. Для частных сумм данного рядаИимеем

Sn = ln 2 + ln 3 + ln 4 + ln

+ + ln

n + 1

+ =

nД

= ln 2 3 4 n (n + 1) = ln(n +

1).

1 2 3

Следовательно,

lim Sn

= lim ln(n +1) = ∞ .

n→∞

→∞

Согласно определен ю 6, ряд является расходящимся.

Пример 3. Исследовать на сходимость ряд

1 .

1 + 1 + 1 + +

+ = ∑

∞

1 3 2 4 3 5

n(n + 2)

n=1

n(n + 2)

Решение. Преобразуем частные суммы данного ряда. Для этого

запишем общий член ряда следующим образом:

n(n + 2)

n + 2

Найдем числа A и B :

A(n + 2)+ Bn

(A + B)n + 2A

n(n + 2)

n + 2

n(n + 2)

Если две равные дроби имеют одинаковые знаменатели, то и их числители равны, т.е.

1 = (A + B)n + 2A или 0 n + 1 = (A + B)n + 2A.

Два многочлена являются равными, если равны коэффициенты при одинаковых степенях неизвестных, т.е.

A + B = 0;2A = 1.

		Откуда A =												1			;			B = −									1			. Тогда an													=			1					1				−			1						;

														2															2																			2											n + 2
						1								2															2																			2			n								n + 2
S1 = a1				=		1							1				;
S1 = a1				=		2		1 −					3				;
						2							3
S2 = a1				+ a2					=			1									1				+			1					1	−			1				;
S2 = a1				+ a2					=			2		1 −							3				+			2					2	−			4				;
												2									3							2					2				4
S3 = a1				+ a2 + a3											=				1						−		1						+	1 1							−		1				+				1				1			−			1			=
S3 = a1				+ a2 + a3											=			2			1				−		3						+					2			−		4				+				2				3			−		5				=
																		2									3							2				2					4								2				3					5
=	1	+	1		−		1			+			1				−			1
=	4	+	2		−		4			+			2				−			5		;
	4		2				4						2							5						1							1					1							1							1								1				1			1
S = a + a + a + a =																										1				+			1		−			1					+		1							1								1				1	−		1
S = a + a + a + a =																														+					−								+				−								+										−			=
	4		1					2						3							4															А																		И
																										4 2												4							2 5															2				4			6
=	1	+	1		−		1			+		1					−			1																								Д
=	4	+	2		−		5			+			2				−			6		;																						Д
	4		2				5						2							6
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
																					и
Sn =			1	+		1			−		1				+			1						−	1						+		1	1					−			1			+ +											1				1						+
			4			2					5							2							6		б2 5															7													2			n −1
	1	1						1								1							1										1							1								1
+				−									=							+						−												+					−												.
+	2			−		n		+ 2					=			4				+			2			−				n + 1								+			2		−				n + 2								.
	2	n				n		+ 2								4							2							n + 1											2						n + 2
										lim Sn										= lim											1		+	1					−				1								+		1					−					1					=
		Отсюда
		Отсюда																													4			2								n +1																			n + 2
											С																				4			2								n +1											2								n + 2
										n→∞														n→∞
= lim			1	−		1 lim								1						−		1 lim											1				=			1		, т.к. lim																1					= 0				и lim		1	= 0.
= lim				−		1 lim														−		1 lim												2			=		4			, т.к. lim																					= 0				и lim			= 0.
	n→∞ 4 2 n→∞ n +1																					2 n→∞ n +												2					4											n→∞ n +1																		n→∞ n + 2
		Следовательно, данный ряд сходится и его сумма равна																																																												1 .
																																											∞		1																								4
		Пример 4. Известно, что ряд																																									∞		1						сходится. Показать, что схо-
																																										∑
																																										∑				5n
																																					1					n=0				5n					1
дится и ряд 54 + 53 + 52 + 5 +1+																																					1			+ +											1						+
дится и ряд 54 + 53 + 52 + 5 +1+																																					5			+ +									5n−4								+
																																					5												5n−4

Решение. Последний ряд получается из ряда

∞

умножением

∑

n=0

на c = 54 , следовательно, он сходится согласно свойству 1.

Пример 5. Исследовать на сходимость ряд

∞

2n + 3n

+ +

2n + 3n

∑

= 2 +

n=0

и, если он сходится, найти его сумму S .

Решение. Данный ряд можно представить в виде

∞

2n + 3n

∞

3 n

∞

∑

n=0

n=0 3

= (1

+ 1)+

Так как ряды

∞

∑

+ +

n=0

∞

= 1

+ +

∑

n=0

являются рядами

геометрической прогрессии, его знаменателями,

меньшими единицы, то они сходятся и их суммы равны соответст-

венно S

′

;

′′

= 2 (см. пример 1).

б1

1−

−

Следовательно, данный ряд сходится по свойству 2 и его сумма

равна S = S′ + S′′ =

2 .

∞

Пример 6. Как известно,

ряд геометрической прогрессии ∑

n=0

является сходящимся. Тогда сходящимся является, например, и ряд 5 + 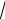2 + 513 + 515 + 516 + + 5n1+1 + , который получается из данного отбрасыванием конечного числа членов: 5 + 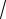2 и добавлением сла-

гаемых: 1+ 15 + 512 + 514 .

Рассмотрим необходимое условие сходимости ряда.

Пример 7. Ряд 24 + 74 + 106 + + 3n2n+1 +

расходится, так как в силу необходимого признака сходимости (свойство 4)

lim a

= lim

≠ 0.

3n +1

n→∞

3 +

При вычислении предела воспользовались тем, что lim 1 = 0 .

n→∞ n

Подчеркнем, что рассматриваемый признак является только необходимым, но не является достаточным, т.е. из того, что общий член

ряда стремится к нулю, еще не следует, что ряд сходится, ряд может и расходиться. Примером такого ряда может служить гармо-

∞ 1

нический ряд ∑

= lim

= 0. Чтобы до-

. Он расходится, хотя

lim a

n=1n

n→∞

n→∞ n

1 n

казать это, напомним, что 1+

< e, т.е.

n +1

< e.

Логарифмируя неравенство по основанию e, получим

n +1

n +1б

< ln e , или nln

Отсюда

n +1

1 .

, или ln(n +1)− ln(n) <

Подставим в

полученное неравенство поочередно n = 1, 2,3,...,

n −1, n.

Получаем неравенства

1 ; ln 4 − ln 3 < 1 ;

ln 2 < 1; ln 3 − ln 2 <

- - - - - - - - - - - - - - - - - - - - - - - - - - -

ln n − ln(n −1)<

,ln(n +1)− ln n < 1 .

n −1

1 / 181 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.84 Mб81799.pdf
#
07.01.2021201.85 Кб018.pdf
#
07.01.2021329.58 Кб0180.pdf
#
07.01.20211.84 Mб21800.pdf
#
07.01.20211.84 Mб01801.pdf
#
07.01.20211.85 Mб151802.pdf
#
07.01.20211.85 Mб21803.pdf
#
07.01.20211.85 Mб111804.pdf
#
07.01.20211.86 Mб21805.pdf
#
07.01.20211.86 Mб11806.pdf
#
07.01.20211.86 Mб31807.pdf