
1770
.pdfгде т± – средняя ионная моляльность электролита. Для электролитов типа КС1, ZnSO4 средняя ионная моляльность совпадает с моляльностью раствора (моль/1000 г Н2О). Для других типов электролитов среднюю ионную моляльность т± вычисляют по соответствующим формулам. Э.Д.С. гальванического элемента при 25° С рассчитывают по формуле
Е Е1 Е2 Е0 Е0 |
0,059 |
lga1 |
0,059 |
lga2 , |
(6.24) |
п |
n |
||||
|
е1 |
|
e2 |
|
|
где Е0 и Е0 – нормальные потенциалы электродов (находят по таблице ряд напряжений); а1 и а2 – активности (для разбавленных растворов концентрации) ионов в растворах. Если nе1=nе2 =ne, то при 25° С
Е Е0 Е0 |
0,059 |
lg |
a1 |
, |
(6.24) |
||||||
п |
|
|
|||||||||
|
|
|
|
|
a |
2 |
|
|
|||
|
|
е |
|
|
|
|
|
|
|
||
при 18°С |
|
a1 |
|
|
|
|
|||||
E E0 E0 |
0,058 |
lg |
. |
|
(6.25) |
||||||
|
|
|
|||||||||
|
n |
|
a |
2 |
|
|
|
|
|||
|
|
e |
|
|
|
|
|
|
|||
При вычислении Э.Д.С. Е от большего потенциала вычитают меньший, руководствуясь данными таблицы ряда напряжений. Таким образом, во всех случаях E>0. На опыте измерение Э.Д.С. гальванических элементов обычно выполняют компенсационным методом. При использовании потенциометрического мостика с реохордной проволокой вычисление Э.Д.С. производят по формуле:
Ех = Ew (AKх/AKW), |
(6.26) |
где Ех – Э.Д.С. исследуемого элемента; Ew – Э.Д.С. нормального элемента Вестона: АКх – отрезок реохордной проволоки при компенсации Э.Д.С. испытуемого элемента; AKW – отрезок реохордной проволоки при компенсации Э.Д.С. элемента Вестона. При 20°С Ew= 1,01830 В; при 25° С Ew= = 1,01807 В. При опытном измерении потенциала отдельного электрода его соединяют в гальваническую пару с электродом сравнения (с нормальным водородным или каломельным) и определяют Э.Д.С. составленной гальванической цепи. Измерив Э.Д.С. этой цепи методом компенсации и зная величину потенциала электрода сравнения, по разности находят потенциал исследуемого электрода. Потенциал нормального водородного электрода условно принимают равным нулю (Е°н2/н+ =0). Потенциал каломельного электрода при заданной температуре и соответствующей концентрации раствора КСl находят по таблице.
Обратимый гальванический элемент, составленный из двух пластинок одного и того же металла, погруженных в растворы солей этого же металла, но с различной концентрацией (активностью) ионов металла, назы-
80
вается концентрационным элементом. Э.Д.С. концентрационного элемента при 18° С вычисляют по формулам:
Еконц |
|
0,058 |
lg |
C1 |
, |
(6.27) |
|
п |
|
||||||
|
|
|
C |
2 |
|
|
|
|
|
е |
|
|
|
|
|
Е |
|
0,058 |
lg |
a1 |
, |
(6.28) |
|
|
|
||||||
конц |
|
п |
|
a |
2 |
||
|
|
е |
|
|
|
|
|
где пе –заряд иона; С1 и С2 – концентрации ионов металла в растворах солей, г·ион/л (C1>C2); a1 и а2 – активности ионов в растворах (a1>a2). Концентрационная цепь может быть составлена из двух водородных электродов, погруженных в растворы с различным содержанием ионов Н+. Потенциометрически можно точно определять концентрацию ионов водорода и рН раствора. При этом используются различные гальванические цепи. Если цепь состоит из водородного электрода, погруженного в исследуемый раствор, и каломельного электрода, то при 25° С
рН=(Ец –Ек.э)/0,059, |
(6.29) |
где Ек.э – потенциал каломельного электрода (с 1 н., 0,1 н. или насыщенным раствором КСl) при 250С.
Для растворов, рН которых не превышает 8, можно применять хин- дронно-водородную, хиндронно-каломельную или хиндроннохингидронную цепи. При хингидронно-водородной цепи рН раствора вычисляют по формуле (t=180C)
рН=(0,6940 – Ец)/0,058. |
(6.30) |
если вместо водородного электрода применен насыщенный каломельный электрод, то при 18°С
рН=(0,4457 – Ец)/0,058. |
(6.31) |
При хингидронно-хингидронной цепи водородный показатель одного из растворов должен быть известен. Обычно применяют буферную смесь (10см3 0,1 н. НСl+90 см3 0,1 н. КСl), рН которой 2,08. Тогда при 180С
рН=2,08+Ец/0,058. (6.32)
Концентрацию веществ в растворе можно с большой точностью определять методом потенциометрического титрования. При этом в ходе титрования непрерывно измеряют Э.Д.С. цепи, составленой из индикаторного электрода, погруженного в исследуемый раствор, и электрода сравнения. Момент эквивалентности определяют по резкому изменению (скачку) Э.Д.С. (безындикаторное титрование).
При работе гальванического элемента протекает определенная химическая реакция. Если химическая реакция протекает обратимо, то при постоянных температуре и давлении получаемая от нее работа будет максимальной полезной работой химического процесса А′макс, которая равна убыли изобарно-изотермического потенциала системы А′макс = –ΔG (2.58). Работа, совершаемая гальваническим элементом в этих условиях, равна
81
Э.Д.С. элемента, умноженной на количество прошедшего электричества, т. е.
|
G neFE , или ΔG=-neFE, |
(6.33) |
Амах |
где пе – число электронов, участвующих в реакции; F – число Фарадея (9,65·107 Кл/кг·экв); Е – Э.Д.С., В. Величина изобарно-изотермического потенциала выражается в Дж/кмоль. Изменение изобарно-изотермического потенциала и максимальную работу можно также рассчитать по тепловому эффекту реакции (Δi = –QP) и соответствующему изменению энтропии ΔS
(2.57):
ΔG=Δi – TΔS. |
|
||
В термодинамике доказывается, что |
|
||
|
д G |
|
|
S |
|
, |
(6.34) |
|
|||
|
дT р |
|
|
т. е. изменение изобарно-изотермического потенциала с температурой, равно частной производной ΔG по температуре при постоянном давлении, определяется изменением энтропии системы. Тогда можно записать, что
|
G i T |
|
д G |
|
|
||||||||
|
|
|
|
|
|
. |
|
(6.35) |
|||||
|
дТ |
|
|
||||||||||
|
|
|
|
|
|
|
|
р |
|
|
|||
Сопоставляя уравнения (6.34) и (6.35) с учетом, что |
|
||||||||||||
|
д G |
|
|
|
дЕ |
|
|
||||||
|
|
|
пеF |
|
|
|
, |
|
|
||||
|
|
|
|
|
|
||||||||
|
дЕ р |
|
|
|
дТ р |
|
|
||||||
получим |
|
|
|
i |
|
|
|
дЕ |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
Е |
|
T |
|
|
|
. |
(6.36) |
|||||
|
n F |
|
|
|
|||||||||
|
|
|
|
|
|
|
дТ |
р |
|
||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
Согласно (6.34)
ΔS=neF(дElдT)p. (6.37)
Математические формулы (6.33), (6.36) и (6.37) связывают основные термодинамические характеристики (Δi, ΔG и ΔS) химических реакций, протекающих в гальванических элементах, с величиной Э.Д.С., которую измеряют с весьма большой точностью.
Пример. Вычислить потенциал медного электрода в растворе, содержащем 0,16 г CuSO4 в 200 см3 воды при 25° С.
Решение. Рассчитываем моляльность раствора
ССиSO4 |
|
mCuSo4 1000 |
|
0,16 1000 |
|
|
|
|
|
|
0,005 |
моль/1000 г Н2О. |
|
200MCuSO |
|
|||||
|
|
|
200 159,6 |
|
||
|
4 |
|
|
|
|
|
По справочнику находим коэффициент активности γ± для 0,005 т
СuSO4: γ±=0,573.
Из формулы (6.23) средняя активность Сu2+ равна
82

|
|
аСи2 CCuSO4 |
0,005 0,573 0,002865. |
|
||
Е0 |
Электродный потенциал вычисляем по формуле (6.21). Значение |
|||||
2 находим по прил. 14: |
|
|
||||
Си / Си |
|
|
0,059 |
|
|
|
|
ЕСи / Си2 |
0,34 |
lg0,002865 0,34 0,075 0,265В. |
|||
|
|
|||||
|
|
2 |
|
|
|
|
|
Пример. Вычислить Э.Д.С. гальванического элемента при 25° С: |
|||||
|
(+) Cu | |
CuSO4 |
|| ТiС14 |
| Тi (–) |
||
|
0,1 моль/1000 г Н2О |
0,01 моль/1000 г Н2О |
||||
|
Решение. По прил. 14находим нормальные электродные потен- |
|||||
циалы для меди и таллия. Используем формулу (6.23). В справочнике находим средние коэффициенты активности солей CuSO4 и Т1С1 указанной моляльности. Для CuSO4 γ±=0,154; для Т1С1 γ±=0,876. Средние активности ионов меди и таллия равны:
аCu2 =0,1·0,154= 0,0154; |
аCu2 = 0,01 · 0,876 =0,00876; |
|
|||
Е 0,34 0,335 |
0,059 |
lg0,0154 |
0,059 |
lg0,00876 0,741 |
В. |
|
|
||||
2 |
1 |
|
|
||
Пример. Вычислить при 18°С Э.Д.С. концентрационного элемента, состоящего из серебряных электродов, погруженных в 0,1 н. и 0,01 н. растворы AgNO3. При этой температуре эквивалентная электрическая
проводимость 0,1 н. AgNO3 9,43 См·м2·кг·экв-1, а 0,01 н. AgNO3 – 10,78 См·м2·кг·экв-1.
Решение. Э.Д.С. концентрационного элемента вычисляем по – формуле (6.27). Для AgNО3 пe=1. По электрической проводимости определяем α0,1 и α0,01 растворов AgNO3.
|
l |
|
l |
|
5,32 6,26 11,58 |
2 |
-1 |
; |
|
|
|
Ag |
|
NO3 |
|
|
См·м ·кг·экв |
|
|
|
|
|
|
|
|
|
|
||
0.1 9,43/11,58 0,814; |
0,01 10,78/11,58 0,931, |
||||||||
Eконц 0,058lg 0,1 0,814 0,0546 В. 0,01 0,931
Пример. При 25° С отсчет на потенциометрическом мостике при включении, элемента Вестона равен 73,7 см, а для элемента, состоящего из нормального каломельного электрода и водородного, погруженного в исследуемый раствор, – 30,2 см. Вычислить водородный показатель раствора.
Решение. Используем формулу (6.29): рН=(Ец – Ек.э)/0,059, Ек25.э для
1 н. КСl находим по прил. 28: Ек25.э =0,2828 В. Согласно (6.26)
Е |
Е |
w |
AKX |
1,01807 |
30,2 |
0,4171 |
В; |
|
|
||||||
ц |
|
AK |
73,7 |
|
|||
W
рН=(0,4171 – 0,2828)/0,059=2,27.
83
Пример. Вычислить ПРAgI при 25° С, если потенциал серебряного электрода, погруженного в насыщенный раствор иодида серебра, равен 325 мВ (относительно водородного электрода).
Решение: Потенциал серебреного электрода равен
Е |
|
E0 |
|
0,059 lgC |
|
Ag / Ag |
|
Ag / Ag |
|
Ag |
|
0,325 0,799 0,059lgCAg
lgC |
|
|
0,474 |
8,0339 |
|
9,9661. |
|
|
|
|
||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
Ag |
|
0,059 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
CAg |
9,249 10 9 г·ион / л. |
|
|
|
|
||||||
Такая же концентрация и ионов иода в |
|
|
|
|
||||||||
растворе: СI- = 9,249·109 г·ион/л. |
|
|
|
|
|
|
||||||
ПР AgI |
|
= |
CAg + CI- |
= (9,249·10-9)2 |
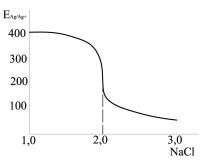
= Рис. 9. Потенциометрическое тит- |
|||||||
= 8,555·10-17. |
|
|
|
|
|
|
рование нитрата серебра хлори- |
|||||
Табличная величина ПР AgI = 8,500·10-17 |
дом натрия |
|
|
|||||||||
|
Пример. Раствор нитрата серебра |
|
|
|
||||||||
потенциометрически титруют 0,5 н. NaCl. Определить содержание |
AgNO3 |
|||||||||||
(мг) в титруемом растворе. Гальваническая цепь |
|
|
|
|||||||||
|
|
|
|
Ag │ AgNO3 │ KNO3 |
│ KCl │ Hg 2 Cl2 |
│ Hg |
|
|||||
|
|
|
|
|
|
|
|
|
1н. |
|
|
|
Объем прибавленного раствора NaCl, см3 |
|
|
|
|||||||||
|
|
|
1,0 |
1,8 |
1,98 |
2,00 |
2,02 |
2,2 |
3,0 |
|||
Е Ag/Ag= относительно нормального каломельного электрода, мВ
383 342 283 224 165 106 64
Решение. Массу AgNO 3 можно вычислить по формуле:
m |
AgNO3 |
T |
vNaCl |
|
NaCl/ AgNO3 |
т.э |
(vтNfCl.э
vтNaCl.э
TNaCl / AgNO3 |
|
NNaClЭAgNO3 |
|
0,5 169,88 |
|
|
|
|
|
|
0,08494 |
г/см3. |
|
|
1000 |
|||||
|
1000 |
|
|
|
||
Объем раствора NaCl, соответствующий точке эквивалентности ), находим по графику с координатами ЕAg/Ag+ – vNaCl (рис.9):
2,0 см3
тAgNO3 0,08494 2,0 0,16988г, или 169,88 мг.
Пример. Рассчитать максимальную работу и изменение энтальпии для гальванического элемента Вестона, если известна Э.Д.С. этого элемента при двух температурах:
84
Т, К …..293 |
298 |
Е, В …..1,01830 |
1,01807 |
Решение: В гальваническом элементе Вестона при работе протекает обратимая реакция:
Cd+Hg2SO4+8/3H2O↔2Hg(ж)+CdSO4 ·8/3H2O.
Число электронов, участвующих в реакции, пе=2; А′макс= –ΔG. Изменение изобарно-изотермического потенциала рассчитываем по формуле
(6.33):
ΔG= –neFE= – 2·9,65·107·1,0183= –1,963·108 Дж/кмоль,
А′макс=1.963·108 Дж/кмоль.
Изменение энтальпии Δi определяем по уравнению (6.36):
|
|
|
|
|
|
|
дЕ |
|
|
|
|
|
|
i neF T |
|
|
Е . |
||
|
|
|
|
|
|||||
|
|
|
|
|
|
дТ р |
|
||
|
|
|
|
|
|
|
|
|
|
Приминаем, что |
|
|
|
|
|
|
|||
|
дЕ |
|
Е |
|
1,01807 1,01830 |
4,6 10 5 В/К, |
|||
|
|
|
|
||||||
|
дТ Т |
5 |
|
|
|
|
|||
Δi=2·9,65·107[293(–4,6·10-5) –1,01830]= –1,991·108 Дж/кмоль.
85
Глава 7. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
7.1. Адсорбция на границе раздела фаз
Коллоидная химия изучает свойства дисперсных систем. Дисперсные системы гетерогенны и обладают сильно развитой поверхностью. Степень раздробленности вещества характеризуется величиной удельной поверхности S0, которая равна отношению общей поверхности частиц S к объему вещества v, подвергнутого дроблению:
S0=S/v. (7.1)
Удельная поверхность – это суммарная поверхность всех частиц вещества, общий объем которых составляет 1 см3. Если принять форму частицы в виде куба с ребром l см, то удельная поверхность
S0 = S/v = 6l2/l3 = 6/l. |
(7.2) |
|||||||
Для частиц шарообразной формы радиуса r |
|
|||||||
S0 |
S |
|
4 r2 |
3 |
|
|
||
|
|
|
|
|
|
. |
(7.3) |
|
v |
4/3 r |
2 |
|
|||||
|
|
|
|
r |
|
|||
По мере раздробления вещества быстро возрастает число частиц, одновременно растет общая и удельная поверхность, а также запас свободной поверхностной энергии в системе. Поэтому в дисперсных системах самопроизвольно протекают адсорбционные процессы, понижающие свободную энергию систем. В растворах адсорбция сопровождается изменением поверхностного натяжения. Адсорбция Г на границе раствор – газ количественно характеризуется избытком вещества (кмоль/м2) в поверхностном слое. Поверхностный избыток Г определяют по изменению поверхностного натяжения, используя уравнение Гиббса:
Г= – (C/RT)(dσ/dC), (7.4)
где С – концентрация раствора, кмоль/м3; R – молярная газовая постоянная, Дж/(кмоль ·К); Т – абсолютная температура; dσ/dC – изменение по-
верхностного натяжения с концентрацией при неизменной поверхности, м2 ·Н/кмоль.
Для приближенных расчетов dσ/dC можно заменить
Δσ/ΔС = (σ2 –σ1)/(С2 – С1),
тогда
r =( –C2/RT)(σ2 –σ1)/(C2 –Ci). |
(7.5) |
При адсорбции на границе раздела твердое тело – жидкость из-за невозможности опытного определения поверхностного натяжения количество адсорбированного вещества рассчитывают по изменению концентрации раствора. Зависимость количества вещества, адсорбированного 1 г адсорбента, от равновесной концентрации при постоянной температуре выражается эмпирической формулой Фрейндлиха:
x/m=aC1/n |
(7.6) |
86
где x – количество адсорбированного вещества, г; т – количество адсорбента, г; С – концентрация раствора при достижении равновесия; а и 1/п – постоянные величины, определяемые опытным путем. Постоянная 1/n для многих адсорбентов и адсорбируемых веществ колеблется в пределах от
0,1 до 0,5.
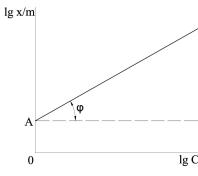
Константа а зависит от природы адсорбируемого вещества и изменяется в широких пределах. Постоянные а и 1/п можно определить графически. Логарифмируя (7.6), получаем уравнение прямой
Ig(х/m)=lgа+l/nIgC. (7.7)
Определив значение х/т при двух концентрациях и построив график в логарифмических координатах, определяют константы а и 1/п (рис. 10):
lg a=0A; 1/n = tg φ.
|
Пример. Определить суммарную |
|
площадь поверхности частиц, если при |
|
дроблении 1 г серы получаются частицы: |
|
а) кубической формы с длиной ребра 10-5 |
|
см; б) частицы шарообразной формы с |
|
поперечником 2 ·10-6 см. Плотность серы |
|
2,07 г/см3. |
Рис. 10. Изотерма адсорбции в |
Решение. Используем формулу (7/2): |
S'0 = 6/l = 6/10—5 = 6 ·105 см-1; |
|
логарифмических координатах |
1 г серы занимает объем 1/2,07=0,4831 см3. |
Суммарная площадь поверхности частиц равна
S1 = 6·105·0,4831 = 2,9·105 см2 = 29 м2.
2. Для частиц шарообразной формы используем (7.3):
S΄΄0 = 3/r = 3 ·106 см-1.
Общая площадь поверхности всех частиц
S2 = 3·106·0,4831 = 1,45·106 см2= 145 м2.
Пример. Определить число частиц, образующихся при раздроблении 0,2 см3 ртути на правильные кубики с длиной ребра 8 ·10-6 см. Плотность ртути равна 13,546 г/см3.
Решение. Рассчитаем массу 0,2 см3 ртути mHg= 0,2 ·13,546 =2,709 г;
Определяем объем одной частицы:
v=l3 = (8 ·10-6)3= 5,12 ·10-16м3
Масса одной частицы будет равна
5,12·10-16·13,546= 6,94·10-15 г.
Число частиц
N |
2,702 |
|
14 |
|
3,9 10 |
. |
|
6,94 10 15 |
|||
|
87 |
|
|
Пример. Определить поверхностный избыток (кмоль/м3) при 10° С для раствора, содержащего 50 мг/л пеларгоновой кислоты CsH17COOH. Поверхностное натяжение исследуемого раствора 57,0 ·10-3 Н/м.
0
Решение. По прил. 26 находим σН2О при 10°С: 10н2о =74,22 ·10-3Н/м. Определяем концентрацию кислоты в растворе С2 =0,05/158 кмоль/м3,
С1=0
|
0,05 |
|
|
|
57,0 10 3 74,22 10 3 |
9 |
|
Г= – |
|
|
|
|
|
7,318 10 |
кмоль/м2. |
158 8,3 10 |
3 |
|
0,05/158 |
||||
|
|
283 |
|
|
|||
Так как Г>0, то адсорбция положительна.
Пример. К 100 см3 раствора уксусной кислоты различной концентрации при 20° С добавили по 3 г активированного угля. Количество кислоты до и после адсорбции определяли титрованием 50 см3 раствора 0,1 н. NaOH. Определить соотношение х/т для каждого из растворов, используя данные титрования:
Объем NaOH, израсходованный на титрование до адсорбции, см3
. . . |
5,5 |
10,6 |
23,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Объем NaOH, израсходованный на титрование после адсорбции, см3 |
||||||||||||||||||||||||
. . . |
1,2 |
3,65 |
10,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. Определяем нормальность, титр и содержание СН3СООН |
||||||||||||||||||||||||
(г) в 100 см3 раствора до и после адсорбции. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
До адсорбции: |
|
|
|
|
|
|
|
N160 |
|
|||||||||||||||
N1 |
5,5 0,1 |
|
0,0111; |
|
T1 |
0,00066 г/см3; |
||||||||||||||||||
|
|
50 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|||||||||||
|
|
|
|
|
|
|
C10 Т1100 0,0660 г (в 100 см3 раствора); |
|||||||||||||||||
N2 |
|
10,6 0,1 |
0,0212; |
|
T2 |
|
N260 |
|
0,001272 г/см3; |
|||||||||||||||
|
|
|
50 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
C0 |
|
|
1000 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T 100 0,1272 г; |
|
|||||||||||
|
|
|
|
|
|
23 0,1 |
|
|
2 |
|
2 |
|
|
N360 |
|
|
|
|||||||
|
N3 |
|
|
|
0,0460 |
; |
T3 |
|
|
0,0276 г/см3; |
||||||||||||||
|
|
|
50 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
C30 |
T3100 0,2760 г. |
|
||||||||||
После адсорбции: |
|
|
N160 |
|
|
|
|
|
||||||||||||||||
|
N1 |
|
|
1,2 0,1 |
|
|
T1 |
0,000144 |
||||||||||||||||
|
|
0,0024 |
|
1000 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
г/см3; |
||||||||||
|
|
|
50 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 T1100 0,0144 г (в 100 см3 раствора); |
|||||||||||||||||
|
2 |
|
3,65 0,1 |
|
|
T2 |
N260 |
0,000438 |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
N |
|
|
|
|
|
|
|
|
|
0,0204 |
; |
|
1000 |
|
|
|
г/см3; |
|||||||
|
|
|
|
50 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
88 |
|
|
|
|
|
|
|
|
|
|
C2 T2100 0,0438 г;
|
10,2 0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T3 |
N360 |
0,001224 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
N3 |
|
|
|
0,0204; |
|
|
|
|
|
|
|
1000 |
|
|
|
г/см3; |
||||||||||||
|
50 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
C3 |
T3 100 0,1224 г. |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Определяем количество кислоты, поглощенное 1 г угля: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
C |
0 |
C |
|
|
|
|
0,0660 0,0144 |
|||||||||||||
x C0 |
C ; |
|
|
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
0,0172 г; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
1 |
1 |
|
|
|
m |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
x |
|
C |
0 |
C |
2 |
|
|
|
0,1272 0,0438 |
||||||||||||
x2 |
C20 |
C2 ; |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
0,0278 г; |
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
x |
|
|
C0 |
C |
|
|
|
|
0,2760 0,1224 |
|||||||||||
x3 |
C30 |
C3 ; |
|
3 |
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
0,0512 г. |
|||||||||
m |
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
Пример. По опытным данным, полученным при изучении адсорбции углем бензойной кислоты из раствора ее в бензоле при 25° С, опреде-
лить графически константы а и 1/n в уравнении Фрейндлиха: |
|
|||
С, ммоль/см3 |
0,008 |
0,025 |
0,053 |
0,118 |
x/m ммоль/г |
0,44 |
0,78 |
1,04 |
1,44 |
Решение. Находим логарифмы С и x/m:
|
|
|
|
|
lgC |
|
|
|
|
|
lg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|||
lg0,006 3,7782 |
–2,2218 |
|
|
|
|
|
|
||||||||
lg0,44 |
|
|
1,6435 |
–0,3565 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
lg0,025 2,3979 |
–1,6021 |
||||||||||||||
lg0,78 |
|
|
1,8921 |
–0,1079 |
|||||||||||
|
|
|
|
|
|
|
|
||||||||
lg0,053 2,7243 |
–1,2757 |
||||||||||||||
lg1,04 0,0170 |
+0,0170 |
||||||||||||||
|
|
|
|
|
|
|
|||||||||
lg0,118 1,0719 |
–0,9281 |
||||||||||||||
lg1,44 0,1584 |
+0,1584 |
||||||||||||||
|
|
|
|
|
|
|
|||||||||
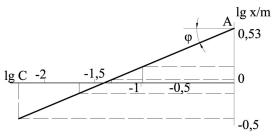
Строим график (рис. 11) в координатах lg x/m – lg C (округляем значения логарифмов до сотых). Отрезок ОА представляет собой lg a в уравнении (7.6), а 1/n является tg φ. Из графика следует, что lg a=0,53, сле-
довательно, а = = 3,4; φ = 22°; tg φ = 0,4040; l/n ≈ 0,4. Для данно-
го случая уравнение (7.6) можно записать так: х/m = 3,4 С0,4.
Рис. 11 Графическое определение констант а и 1/л в уравнении Фрейндлиха
89
