1671

ционно в методе двух изображений рассматриваются вопросы ото­ бражения геометрических свойств кривых линий, алгебраических и неалгебраических, в целом. Свойства же в малом остаются, как пра­ вило, вне поля зрения. Лишь слегка затрагиваются проекционные свойства касательной к кривой линии и отображение кривизны кри­ вой в кривизну ее проекции [2J. Вместе с тем, моделирование кривых линий на чертеже Монжа, будучи задачей теоретического и практиче­ ского смысла, должно позволять:

1. Определять геометрические свойства в целом и в малом моде­ ли кривой линии по самой кривой;

2. Восстанавливать геометрические свойства в целом и в малом кривой линии по ее модели.

Рассмотрению некоторых из обозначенных задач геометрическо­ го моделирования пространственных кривых линий и вопросов, спо­ собствующих их решению, посвящена настоящая глава.

На чертеже Монжа алгебраическая или трансцендентная поверх­ ность моделируется, как известно, некоторым соответствием, уста­ навливаемым между полями горизонтальных и фронтальных проек­ ций точек этой поверхности. Так, например, алгебраическая поверх­

ность Ф" /7-го порядка моделируется (/г-и)-значным соответствием

F"~" п-го порядка [15]. Например, сфера Ф2 моделируется двузнач­ ным квадратичным соответствием F22~2 между полями {АЛ и {А2}

проекций точек АеФ2 [15]. Если линия а принадлежит сферической поверхности Ф2 , то ее моделью на чертеже Монжа будет пара пло­ ских линий я, и а2 - ортогональных проекций линии а, точечно со­ ответственных в квадратичном соответствии F2~2. Обобщая на слу­

по соответственных в соответствии F"". Таким образом, если про­ странственная кривая рассматривается как принадлежащая некоторой поверхности, то ее моделирование на чертеже Монжа необходимо выполнить на основе соответствия, которым моделируется сама по­ верхность.

Если кривая линия а пространства рассматривается как линия пересечения двух поверхностей Ф и ¥, то ее моделью на чертеже Монжа является пара ортогональных проекций а, и а2 - плоских ли­ ний, точечно соответственных одновременно в двух соответствиях, каждое из которых моделирует на чертеже Монжа одну из поверхно­ стей - Ф или ¥. В частности, если а есть линия пересечения по­ верхности Ф и плоскости, то ее модель - пара линий а, и а2 , точечно соответственны в родстве, моделирующем плоскость, и в соответст­ вии, моделирующем поверхность Ф.

Если линия а пространства рассматривается как линия пересе­

- линий, точечно соответственных в двух вырожденных соответстви­ ях, одно из которых моделирует проецирующую цилиндрическую по­ верхность Ф, а другое - ¥.

Вышеизложенный подход к моделированию поверхностей и ли­ ний, им принадлежащих, не так давно обозначен в классической на­ чертательной геометрии [15, 16] и основан на теории многозначных соответствий, которая до настоящего времени изучена недостаточно.

5.2.2.Проекционные свойства осей подвижного трехгранника

пространственной кривой

При конструктивном и аналитическом моделировании на плоско­ сти алгебраических и неалгебраических плоских и пространственных кривых линий их свойства в целом и дифференциальногеометрические свойства (свойства в малом) преобразуются в соот­ ветствующие свойства моделей (проекций) этих кривых. Очевидно,

эти свойства моделей зависят как от свойств в целом и в малом моде­ лируемых кривых, так и от соответствующих свойств аппарата моде­ лирования (проецирования). Задача исследования указанных свойств моделей кривых линий известна в начертательной геометрии [2, 16], однако считать ее полностью решенной нет оснований. Обратная за­ дача - восстановление указанных свойств кривых линий по их моде­ лям, является новой и ожидает своего решения.

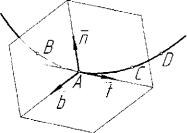
Пространственные кривые линии, в отличие от плоских линий, не могут быть помещены всеми своими точками в плоскость. Плоскости множества плоскостей, каждая из которых проходит через тройку то­ чек пространственной кривой линии, различаются между собой по­ ложением и ориентацией в пространстве. Возьмем на пространствен­ ной кривой линии четыре обыкновенные точки A,B,C,D (рис. 5.32). В дифференциальной геометрии пространственной кривой линии из­ вестно, что предельное положение

плоскости, проходящей через три бесконечно близко расположенные точки B,C,D на кривой линии, ко­ гда эти точки стремятся к точке А, называется соприкасающейся плос­ костью кривой в точке А [26]. Роль соприкасающейся плоскости заклю­ чается в том, что среди всех плоско­ стей, проходящих через точку А кривой, она наиболее плотным об-

разом прилегает к кривой, т.е. в бесконечно малом около точки А пространственная кривая может быть рассмотрена как плоская линия, принадлежащая соприкасающейся плоскости. Нормаль п в точке А кривой, расположенная в соприкасающейся плоскости, называется главной нормалью, а нормаль Ь, перпендикулярная в точке А к со­ прикасающейся плоскости (n,t), называется бинормалью. Образую­ щиеся в точке А пространственной кривой плоскости (п,Ь) и (t,b),

называются соответственно нормальной и спрямляющей плоскостью

кривой. Совокупность трех прямоугольных координатных осей t , п, h и трех координатных плоскостей (п,t), (n,b) и (t,b) называется подвижным трехгранником пространственной кривой в се обыкно­ венной точке А. Его положение в пространстве меняется при движе­ нии точки А по кривой линии. Этот трехгранник называют трехгран­ ником Френе, по имени впервые предложившего его в 1874 году французским математиком Жаном Фредериком Френе (1816 - 1900).

Рассмотрим проекционные свойства осей трехгранника Френе для случая линейного проецирования. Пусть 5 и П - соответственно центр и плоскость проецирования (рис. 5.33). Для пространственной

надлежащий соприкасающейся плоскости кривой а в ее точке 2, и Ь2 - вектор бинормали. Очевидно, секущей 1 - 2 кривой линии а вза­ имно однозначно соответствует секущая Г-2' линии а', секущей 2 - 3 взаимно однозначно соответствует секущая 2 - 3 ' и т.д. Точки пересе­ чения пар соответственных секущих образуют на плоскости проекций II некоторую линию соответствия а". Очевидно, при стремлении точки 1 по линии а к фиксированной точке 2, точка Г будет стре­ миться к фиксированной точке 2' и ттредельному касательному поло­ жению г2 секущей 1 - 2 будет соответствовать предельное касатель­ ное положение г'2 секущей Г-2', при этом секущая Г - 2 " будет зани­ мать предельное касательное положение г"2 в точке 2 " е а " . Из ска­ занного следуют выводы:

1. В общем случае линейного проецирования (Sea исключает­ ся) касательная к кривой линии пространства проецируется в каса­ тельную к проекции этой кривой, т.е. t2 -> t\ ;

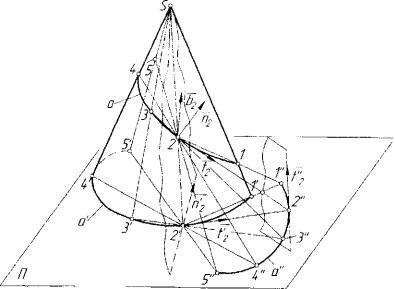
2. Соприкасающаяся плоскость кривой линии пространства в ее обыкновенной точке определяется касательной к этой кривой и соот­ ветствующей касательной к линии соответствия на плоскости проек­ ций, т.е. (/2, «2.) = (f2 ,г" 2 ) .

Нормаль п2 к кривой линии а пространства в общем случае не

отображается в нормаль п\ к проекции а' этой линии в их соответст­

вующих точках. Действительно. Пусть п\ - нормаль в точке 2' цен­

тральной проекции d линии а. Плоскость (S, п\ ) - плоскость про­

ецирования для нормали п\ , при этом (S, п\) в общем случае не

перпендикулярна плоскости проекций П. Предположим, что нормаль

п2 к линии а в точке 2 6 а , соответствующей точке 2 ' G O 1 , принад-

Рис. 5.33. К обоснованию проекционных свойств осей подвижного трехфанника

лежит плоскости (S, п\ ). Очевидно, что п2 будет единственной нор­

малью, расположенной на прямой п2 пересечения двух плоскостей:

264

плоскости проецирования (5,ri 2 ) и нормальной плоскости (п2,Ь2)

птнии а в ее точке 2. Но через касательную прямую t2 к линии на конической поверхности (S,a) можно провести пучок соприкасаю­

щихся плоскостей, каждая из которых соответствует определенной

линии на поверхности (S,a), т.е. касательная прямая t2 является об­ щей касательной для множества кривых на поверхности (S, а) в их

общей точке 2, при этом линия а' является общей центральной про­ екцией всех этих кривых линий. Поскольку каждая кривая линия на поверхности (S,a) из множества линий с общей касательной прямой

/, имеет свою определенную нормаль п2 в точке 2, то в точке 2 е а образуется пучок нормалей п2 , соответственный вышеуказанному пучку соприкасающихся плоскостей, т.е. определенной нормали п2

пучка соответствует определенная соприкасающаяся плоскость из пучка таких плоскостей. Следовательно, в общем случае (особые слу­ чаи Sea и ?2 // П исключаются из рассмотрения) нормаль к кривой линии пространства не проецируется в нормаль к центральной проек­ ции этой линии в их соответствующих точках. Лишь в единичном

случае, рассмотренном выше, когда п2 принадлежит плоскости

(S,n'2), нормаль к кривой линии принадлежит проецирующей плос­ кости (S, п'2).

5.2.3.Кривизна и кручение пространственной кривой

Предположим, что пространственная кривая линия состоит из обыкновенных точек (рис. 5.34, а). Для каждой из этих точек может быть построен трехгранник Френе (t ,n,b) пространственной кривой. Если свести все единичные векторы касательных t и бинормалей b

кривой линии в некоторую точку S пространства, то получим сфери­ ческие индикатрисы et и еь касательных и бинормалей кривой, при­ надлежащие единичной сфере (рис. 5.34, б, в). Расстояние s'm между точками 0 и 1, измеренное по индикатрисе еп представляет собой

165

угол ог01 между единичными касательными векторами /0 и /,, а рас­

стояние 5*, между точками 0 и 1, измеренное по индикатрисе еь,

представляет собой угол в0] между единичными векторами Ь0 и Ь{

бинормалей. Очевидно, непрерывному изменению положения точки

дифференцирусмостью (рис. 5.35, а, б). Они называются уравнениями кривой в естественных координатах [2, 26].

/,,/ ; "

вектора t касательной в данной точке кривой по отношению к пути

As, проходимому точкой по кривой, и называется кривизной в данной

точке. Очевидно, А:>0. Величина —-R представляет собой радиус

к

соприкасающейся с пространственной кривой линией окружности,

(рад)

SIMHI

а) б)

Рис. 5.35. Графики уравнений кривой в естественных координатах

принадлежащей соприкасающейся плоскости кривой в данной точке. Центр этой окружности принадлежит главной нормали п кривой и является ее центром кривизны в данной точке [26].

Величина lim ^ = |%\ представляет собой скорость вращения

Д А ' - » О

вектора b бинормали или соприкасающейся плоскости (1 , п) в дан­ ной точке кривой по отношению к пройденному точкой пути As, и называется модулем кручения кривой в данной точке [26].

Различают пространственные кривые положительного (х > 0) и отрицательного (х < 0) кручения. Существует наглядное правило оп­ ределения кривых / > 0 и кривых х < 0 (рис. 5.36, а, б).

Рис. 5.36. Кривые различных по знаку кручений

Выберем направление смещения точки по кривой линии, опреде­ ляемое вектором t ее касательной, таким образом, чтобы закругле­ ние кривой при этом смещении происходило со стороны вектора b против часовой стрелки. Тогда при х > 0 происходит переход кривой линии в рассматриваемой точке с задней стороны соприкасающейся плоскости (t, п) на переднюю, а при ^ < 0 - с передней стороны со­ прикасающейся плоскости на заднюю. Выбор точки зрения, с перед­ ней или с задней стороны соприкасающейся плоскости, для различе­ ния кривых / > 0 и / < 0 н е имеет значения. Знак кручения х зави­ сит лишь от геометрической формы кривой линии. В дифференциаль­ ной геометрии известна теорема, согласно которой две кривые в про­ странстве отличаются лишь положением в пространстве, если (после согласования начальных точек и направлений отсчета на них) их на­ туральные уравнения к = Fk(s) > О и х = ^С<) одинаковы [26].

Представление о геометрической форме пространственной кри­ вой вблизи ее обыкновенной точки можно получить, рассматривая

ортогональные проекции кривой на плоскостях сопровождающего трехгранника Френе в этой точке. Пусть в исследуемой точке кривой

выполнены условия к > О, J * О, которыми исключаются точки рас­ прямления (А = 0) и плоскостной характер (х = 0) кривой. Исследо­

вание формы кривой удобнее вести на основе ее векторного уравне­

А'. Записав разложение этого приращения но формуле Тейлора по степеням As, получим выражение вектора смещения АА ':

AZ4' = r-As+] r-(As)2 +-r-(As)3 +...,

168

н котором г, г, г, ... - последовательные производные радиусвекто­ ра r(s) по аргументу S. Учитывая соответствующие выражения для этих последовательных производных [26], получим формулу:

dk

в которой А: = -. От этой формулы путем группировки по векторам ds

7' ,п н b перейдем к окончательной и пригодной для рассматривае­

Рассмотрим вначале проекцию ет кривой е на соприкасающуюся плоскость ( г , и ) . Очевидно, векторное уравнение ортогональной про­ екции е,„ будет получено, если в формуле для АА' отбросить со­ ставляющую по бинормали Ь:

~АА'т = 7 • {As + ...} + «• | ^ *( А»')2 + • • j •

Анализ этого уравнения показывает, что точка Л',„ описывает

кривую е,„ (рис. 5.37, б)) со смещениями по векторам t и и соответ­ ственно 1-го и 2-го порядков малости относительно As. Поскольку

кривизна исходной кривой е определяется в соприкасающейся плос­

кости, то кривизна ортогональной проекции ет и самой кривой е имеют одно и то же значение в точке А.

Проекция кривой е на спрямляющую плоскость (7 , Ь) представ­ ляет собой линию eth, уравнение которой получается исключением из общего уравнения смещения АА' его составляющей по вектору нор­ мали п\

AA'lh = 7 • {As +...} + b • Ц ky(Asf + . . . j .

Анализ этого уравнения показывает, что точка А\ь описывает

кривую etb со смещением по векторам t и Ъ соответственно 1-го и

169

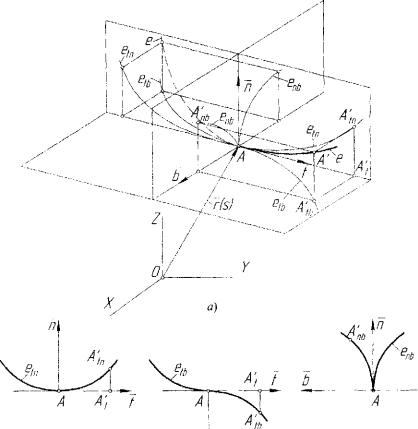
3 го порядков малости относительно As. Следовательно, прямая АА\

имеет с кривой eth касание 2-го порядка, т.е. точка А является точкой распрямления и кривая etb расположена по обе стороны касательной прямой АА\, так как коэффициент при Ъ меняет свой знак при смене знака у As (рис. 5.37, в).

ч2?

б) в) г)

Рис. 5.37. Ортогональные проекции кривой на гранях трехгранника Френе

170

Проекция кривой е на нормальную плоскость (п,Ь) представляет собой линию епЪ, уравнение которой получается из общего уравнения смещения А А исключением составляющей по касательной t :

~Mnh = п-11 k(Asf + ...J + b • | i ^ ( A 5 ) 3 +...] •

Анализ этого уравнения показывает, что точка А'пЬ описывает

кривую епЬ со смещением по векторам nub соответственно 2-го и

3-го порядков в малом относительно As-. Составляющая смещения по вектору п направлена в сторону этого вектора (&>0,(А<;)" > 0 ) , т.е. проекция enh находится с одной стороны бинормали Ь. Составляю­ щая смещения по вектору b меняет свой знак со сменой знака Ду при фиксированном знаке кручения % > т-с- о п а расположена по обе сто­ роны главной нормали п. Поскольку составляющая по Ъ есть беско­ нечно малая более высокого порядка малости относительно As\ чем составляющая по п, то проекция еп1> более плотно примыкает к век­ тору главной нормати /?, чем к вектору бинормати Ъ. Имеет место ючка возврата 1-го рода (рис. 5.37, г).

Различные виды пространственных кривых линий, обладающих определенными дифференциально-геометрическими свойствами, рассмотрены в работах [2, 26].

5.2.4.Кривизна ортогональных проекций кривой линии

стью до знака определяют направления ортогонального проецирова­ ния на плоскости проекций Я, и П-, соответственно. В таком случае уравнение проекции я, будет иметь вид:

171

значные, непрерывные и дифференцируемые. В таком случае могут быть определены следующие производные вектора г\ :

Кривизна кх кривой ах может быть выражена известной форму­ лой [26]: А, = jr, "[. Отсюда следует формула:

(h )

Последнее равенство равносильно следующему:

и на их основе получить другие выражения, имеющие место в этой формуле:

/••г; - |/ - ( Л *)*]•[*:«-(*«•*)*] = -*(/ -А)-(и-Л);

(/^ -/^)2 = А2(г -А)2 -(п-к)2.

Подставим (5.3), (5.4), (5.7), (5.8) и следующие за ними выраже­ ния в формулу (5.5) и выполним необходимые преобразования. В ито­ ге получим выражение:

к2\\-(п-к)2-(7-к)2 +(Т-к)2 -(п-к)2]-к\Т-к)2 -(ri-lcf_ =

Аналогично для проекции а2 можно получить формулу ее кри­ визны:

173

где b - единичный вектор бинормали кривой а. Из формулы (5.9) следует:

1. В случае плоской кривой а величина J6 • к\ есть постоянная и

представляет собой косинус угла наклона плоскости кривой к плоско­ сти проекций Я,, а в случае пространственной кривой а - косинус утла наклона соприкасающейся плоскости ( ( , « ) к //,;

2.Величина |/ хк\ есть косинус угла наклона касательной кри­

вой линии а к плоскости проекций Пх.

Содержание п.п. 1 и 2 соответствуют известным в начертатель­ ной геометрии результатам исследования ортогональных проекций пространственной кривой, полученными из иных соображений [2].

Учитывая координатное представление каждого из единичных векторов / и b [26], уравнения (5.9) и (5.10) можно преобразовать к виду, удобному для практического вычисления кривизны ортогональ­ ных проекций а} и а2 исходной пространственной кривой а :

Последние формулы с точностью до обозначений производных совпадают с известными формулами определения кривизны плоской кривой [261, заданной параметрическими уравнениями х = x(t), у - y(t), где параметр t - не длина дуги этой кривой. В (5.11) диффе­ ренцирование производится по параметру S (длина дуги пространст­ венной кривой а), который выполняет роль параметра t для проек­ ции этой кривой. Вычисление кривизны по формулам (5.11) возможно только в заведомо обыкновенных точках кривых ал т а2, поскольку для них имеет место соответственно t\ * 0; г2 * 0, а также в их точках

174

распрямления, необходимым и достаточным условием существования

Предположим, что а, и а2 - две плоские кривые, рассматривае­ мые как заданные ортогональные проекции некоторой кривой а про­ странства. Пусть эти кривые описываются векторными уравнениями: /[ = г,( . 9,), где s0i < 5 , < 5 n l ; r2 =r2(s2), где д02 < s2 <sn2. В таком слу­ чае из проекционной схемы на рисунке 5.38, а также существования однозначных, непрерывных и дифференцируемых функций .v, - Jx(s), s2 = f2(,s), следует:

что позволяет определить единичный касательный вектор искомой

точками, как и прежде, обозначено дифференцирование по параметру s. Очевидно, для определения вектора t в точке Аеа с параметром s, необходимо выполнение для этой точки хотя бы одного из усло-

175

вует достаточному признаку существования обыкновенных точек [26]

Последнее уравнение позволяет преобразовать выражение (5.20) к виду:

ние выражения (5.21) также приводит к выражению второй производ­ ной:

+Пк2(^)2. ds

Уравнения 5.13, 5.14, 5.21, 5.22, 5.23 и 5.24 определяют положе­ ние трехгранника Френе кривой линии в сс текущей точке по ортого­ нальным проекциям этой кривой.

Рассмотрим пример. Выберем в качестве линий а, и а2 окруж­

ность и косинусоиду соответственно (рис. 5.39). Уравнения линииat

Учитывая это обстоятельство и используя известные вычислительные формулы для единичных векторов касательных и нормалей плоских

метров в (5.21), (5.22), (5.23) и (5.24), на основании (5.25) получим из­ вестную формулу [26] для вычисления кривизны цилиндрической винтовой линии: к = R(R2 + /и2ух.

Определение кручения кривой линии а по заданным ее проекци­ ям at и а2 представляет собой более сложную задачу, чем определе-

мне се кривизны к. Решение этой задачи может быть выполнено на основе дифференцирования выражения (5.13) по параметру S.

Отметим, что задача восстановления кривизны и кручения кри­ вой линии по ее модели - пары взаимосвязанных ортогональных про­ екций, в учебной и научной геометрической литературе не рассмат­ ривалась.

5.2.6.Проекционные свойства алгебраических кривых

Кроме общих проекционных свойств, характерных для неалгеб­ раических и алгебраических пространственных кривых, вытекающих из соответствия геометрий в малом пространственной кривой и ее проекций, алгебраические кривые дополнительно обладают проекци­ онными свойствами, которые отражают соответствие алгебраических характеристик этих кривых и их проекций [15, 16]. Приведем основ­ ные из них.

1.Для центрального проецирования в общем случае порядок ал­ гебраической кривой равен порядку ее проекции.

Как известно, порядок п пространственной алгебраической кри­ вой равен числу точек ее пересечения с произвольной плоскостью пространства. Проведем плоскость через центр проецирования. Эта плоскость пересечет кривую в П точках. В силу однозначности цен­ трального проецирования и-точек пересечения отобразятся в п точек пересечения прямой линии - следа проведенной проецирующей плос­ кости, и проекции пространственной алгебраической кривой линии на плоскости проекций.

2.Если центр проецирования является / -кратной точкой алгеб­ раической кривой порядка п, то порядок криволинейной составляю­ щей проекции кривой равен n — i. Действительно. Через / -кратную точку проходят г ветвей алгебраической кривой. Возьмем на каждой ветви по две точки, бесконечно близко расположенные к i -кратной точке. Эта тройка точек на каждой ветви определяет плоскость, пре­ дельным положением которой является соприкасающаяся в / - кратной точке плоскость этой ветви. Таким образом, в / -кратной