1671

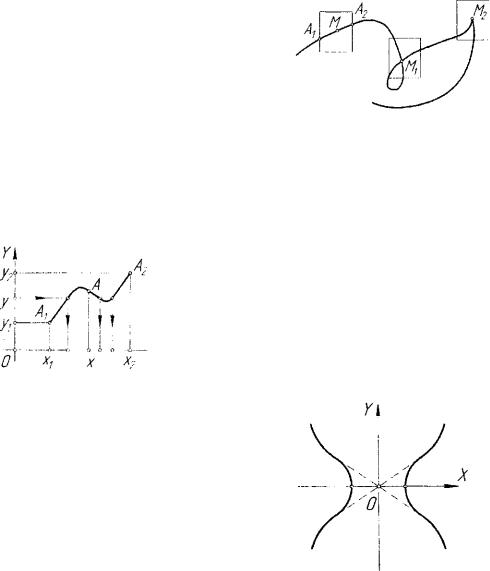
На основании вышеизложенного рассмотрим вначале моделиро­ вание на плоскости кривой линии пространства Е3.

5.1. Плоские кривые линии

Из аналитической геометрии известно, что если ввести на плос­ кости декартову систему координат X, Y, то одно уравнение между текущими координатами точки F(x, у) = 0 в общем случае определя­ ет на плоскости геометрическое множество точек — кривую линию. В начертательной геометрии, с точки зрения геометрического представ­ ления, кривая линия считается плоской, если все ее точки принадле­ жат плоскости.

5.1.1.Типы точек плоской кривой

ной, непрерывной и дифференцируемой [26]. Геометрический смысл определения простого отрезка кривой ясен из рисунка 5.1. Функция f(x) определяет взаимно однозначное отображение отрезка [х,,х2] прямой линии на отрезок [ Л , , ^ ] кривой линии. Непрерывность и дифференцируемость функции f(x) обеспечивают плавный ход кри­ вой линии на отрезке [А{,А2], исключающий появление точек само­ пересечения (точка М,) и других особых точек (рис. 5.2). Очевидно,

кривой линии имеет вид простого отрезка. В этом прямоугольнике

называются особыми. Точки Мх и М2 на рисунке 5.2 являются осо­ быми.

Особые точки кривой линии могут двойными, тройными и т.д. гонками [26]. Укажем типы и примеры двойных особых точек пло­ ской кривой.

1. Изолированная точка, определяемая как точка самопересече­

X

'0

\

\

Рис. 5.3. Изолированная точка кривой

геометрическую интерпретацию - она представляет собой сечение (нулевая окружность) кругового конуса плоскостью, проходящей че­ рез его вершину. Это сечение представляет собой пару мнимых (изо­

ки возврата первого рода (рис. 5.5, а)) и точки возврата второго рода

(рис. 5.5, 6)). На первом рисунке изображена полу кубическая парабо­ ла у2 -х3 = 0 , на втором - кривая (у-х2)2 - х 5 = 0 .

X

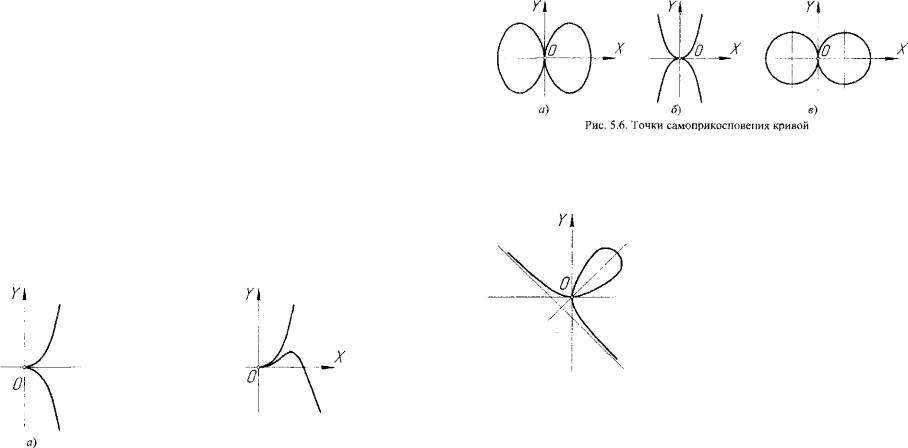
собой две касающиеся параболы (рис. 5.6, б)), у кривой, состоящей из двух касающихся окружностей, и представляющей собой осевое се­ чение поверхности тора, образующая окружность которого касается оси Y вращения тора (рис. 5.6, в)).

В зависимости от вида уравнения, записанного в декартовой сис­ теме координат, кривая линия может быть алгебраической или транс­ цендентной [16]. Нераспадающаяся алгебраическая кривая порядка п

Xвторого порядка не могут иметь осо­ бых точек. Кривая третьего порядка

точку - точку самопересечения (рис. 5.7).

5.1.2.Элементы дифференциальной геометрии плоской кривой

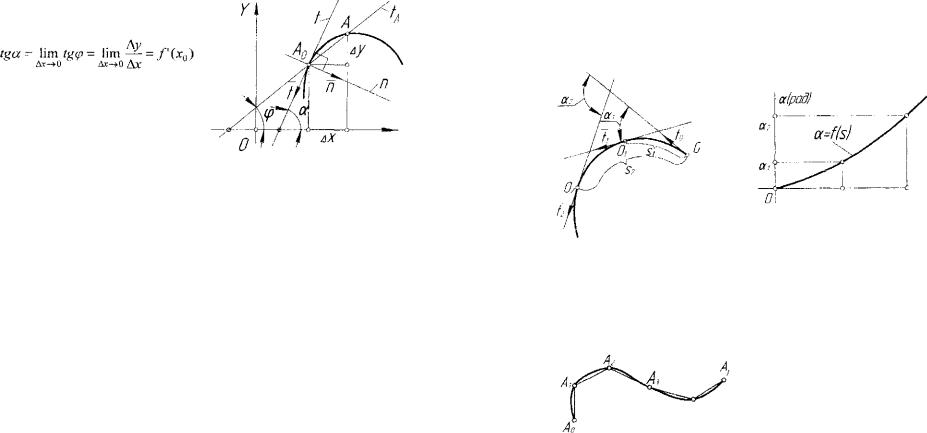
Известно, что вблизи обыкновенной точки /10(х0,у0) кривая ли­ ния имеет вид простого отрезка и может быть выражена уравнением v = / ( х ) . Точка А на простом отрезке кривой определяет ее секущую

кривой [2]. Очевидно, для окружности радиуса R таким графиком

1 оудет прямая линия a = — s.

R

стремится периметр ломаной, вписанной в кривую линию, при таком неограниченном возрастании числа звеньев ломанной, когда длина наибольшего из звеньев стремиться к нулю.

Как следует из рисунка 5.9, а) при движении точки по кривой происходит непрерывное изменение величин s (удаление движущей­ ся точки по кривой от ее начального положения) и а (угол поворота касательной относительно ее начального положения). Степень ис­ кривленности кривой линии характеризуется ее кривизной к , опре-

125

дельной касательной окружности называется радиусом кривизны кривой в ее точке касания с этой окружностью, а сама окружность на­ зывается окружностью кривизны. Взаимное расположение окружно­ сти кривизны и кривой в точке их касания таково, что окружность кривизны в этой точке одновременно пересекает кривую и касается ее, то есть имеет место касательное пересечение [26].

Если построить график функции а = f (s) изменения параметров а и s кривой т, то можно определить кривизну кривой в любой ее обыкновенной точке (рис. 5.12, а, б). Определим, например, кривизну

Рис. 5.12. Изменение кривизны кривой линии и эволюта кривой

5.7.3.Эволюта и эвольвента. Касание кривых

Геометрическое место центров кривизны плоской кривой линии представляет собой кривую линию е, которую называют эволютой данной кривой т (рис. 5.12, а)). Эволюту определяют также как оги­ бающую нормалей данной кривой. Первоначальная кривая относи­ тельно своей эволюты называется эвольвентой. Из геометрической схемы образования эволюты следует известное в дифференциальной геометрии [26, 34] равенство, определяющее взаимосвязь эвольвенты и эволюты: 77,Е2 - R2-Ri, где ЕХЕ2- длина дуги кривой между точ­ ками Ех и Е2 эволюты; 7?,, R2 - радиусы кривизны эвольвенты т в се точках Л{ и А2 соответственно. Приведенное равенство может быть представлено следующим образом: EtE2 = (R2 + с ) - ( Л , + с), где с - действительное число. Из последнего равенства следует, что, вопервых, через каждую точку касательной к эволюте проходит единст­ венная эвольвента, во-вторых, для одной и той же эволюты существу­ ет однопараметрическое множество эвольвент. Поскольку касатель­ ные к эвольвентам этого множества в их соответствующих точках

127

(точках, принадлежащих одной общей нормали эвольвент множества) параллельны, то эвольвенты множества представляют собой парал­ лельные кривые.

Взаимосвязь геометрий эвольвенты и эволюты позволяет подойти к важному, с точки зрения теории и практики, понятию касания (со­ прикосновения) кривых линий. Касание двух кривых линий характе­ ризуется наличием у них в общей точке общей касательной и общей нормали (рис. 5.13).

точке имеется только общая касательная, то кривые имеют касание первого порядка (рис. 5.14, а)), для которого характерно несовпадение точек касания эволют еа и ев с общей нормалью п линий а и в со­ ответственно.

Если у касающихся кривых а и в в их общей точке совпадают касательные и их эволюты еа и ев имеют касание первого порядка, то первоначальные кривые а ж в имеют касание второго порядка, то есть у них имеются общая касательная в общей точке и один радиус кривизны (рис. 5.14, б)).

Если у касающихся кривых а и в в их общей точке совпадают касательные, их эволюты еа1 и ев1 первого порядка имеют касание второго порядка, то есть эволюты еа2 и ев2 второго порядка имеют касание первого порядка, то первоначальные линии а й в имеют ка­ сание третьего порядка и т.д. (рис. 5.14, в)).

Таким образом, если у двух касающихся кривых линий порядок их касания равен п, то в их общей точке касания первый порядок ка­

первого порядка.

В технике нашли различные применения эвольвенты окружности. Так, например, профили зубьев колеса и шестерни в зубчатой переда­ че в сечении плоскостью, перпендикулярной их осям, очерчены по дуге эвольвенты окружности, вследствие чего такая зубчатая переда­ ча называется эвольвентой . Впервые она была предложена Л. Эйле­ ром в 1767 году.

5.1.4.Способы образования ппоских кривых линий

При решении множества различных теоретических и практиче­ ских задач возникает необходимость в получении информации о форме и геометрии плоской кривой линии, определяемой условиями задачи. Одна и та же кривая линия может быть определена различны­ ми условиями, каждое из которых выводит на определенный способ образования (конструирования) этой кривой. Из множества способов, различающихся теоретическим обоснованием и конструктивной реа­ лизацией, можно выделить основные, наиболее часто применяемые. К ним относится нижеследующие способы образования кривых линий.

1.Кривая линия определяется как линия сечения поверхности плоскостью. Например, кривые второго порядка издревле определя­ лись греками как сечения кругового конуса различными плоскостями.

2.Кривая линия рассматривается как проекция (линейная: цен­ тральная, параллельная, ортогональная, или нелинейная: косая, окружностная, винтовая и др.) пространственной или плоской кривой линии на плоскость, например, центральные проекции окружности - это кривые второго порядка. Кривая может быть рассмотрена как вы­ рожденная проекция (след) поверхности на плоскости, например, окружностная проекция кругового тора на его осевую плоскость - две окружности.

3.Кривая линия определяется как геометрическое множество точек, подчиненных определенному метрическому условию. Напри­ мер, Евклид рассматривай конические сечения (эллипс, гипербола, парабола) как геометрические места точек, сохраняющихся постоян­ ное отношение расстояний от данной точки (фокуса) и от данной прямой (директрисы).

4.Кинематический способ. В этом случае плоская кривая рас­ сматривается как траектория движения точки по определенному зако­ ну. Например, циклоидальные кривые представляют собой траекто­ рии точки, жестко связанной с окружностью некоторого круга, кото­ рая катится без скольжения по окружности другого круга. Кинемати­ ческий способ образования кривых был положен Декартом в основу определения кривых методом координат. В кинематической геомет­ рии изучаются различные кинематические способы образования кри­ вых линий [8].

5.Кривая рассматривается как множество точек пересечения линий двух проективных пучков. Например, в проективной геометрии известна теорема Штейнера [10, 37], согласно которой кривая второго порядка представляет собой множество точек пересечения соответст­ вующих прямых двух проективных пучков прямых первого порядка (рис. 5.15), включая центры пучков. В частности, если угол в паре лу­ чей первого пучка равен углу в паре соответствующих им лучей вто­ рого пучка, то получаем проективное образование окружности, если

при этом вращение лучей в обоих проективных пучках имеет одно направление. Если вращение разное, то получаем гиперболу [37J. Кривая третьего порядка, применяемая в синтезе плоских механизмов [8], определяется как множество точек пересечения соответствующих элементов двух проективных пучков:

пучка прямых первого порядка и пучка кривых второго порядка. Два проек­ тивных пучка кривых второго порядка определяют кривую четвертого поряд­ ка и т.д., то есть кривые высших по­ рядков образуются при помощи проек­ тивных пучков кривых низших поряд­ ков.

6. Кривая определяется заданием ее дифференциально-геометрических свойств, то есть свойств, определяю­ щих геометрию кривой в матом. По

условию задачи составляется соотношение между бесконечно матыми элементами линии в виде дифференциального уравнения, после­ дующее интегрирование которого приводит к обычному уравнению кривой [29]. Например, трактриса представляет' собой кривую, у ко­ торой длина отрезка полукасательной есть постоянная величина а

(рис. 5.16). Изначальное дифференци­ альное уравнение этой кривой имеет

ОР после интегрирования, параметриче­

7.Кривая рассматривается как образ линии в заданном преобра­ зовании плоскости (аффинном, проективном, центральном нелиней­ ном и др.) [16]. Например, в квадратичном преобразовании плоскости образом прямой линии является кривая второго порядка [8, 16]; обра­ зом окружности в родстве является эллипс [37].

8.Кривая линия представляет собой график некоторой функции, которая может быть задана аналитически, то есть уравнением. На­ пример, к кривым, которые первоначально определялись уравнения­

5.1.5.Общие свойства плоских алгебраических кривых

Множеству уравнений, связывающих две переменные координа­ ты в декартовой системе координат, соответствует множество пло­ ских кривых. В зависимости от вида уравнения (алгебраическое или трансцендентное), записанного в декартовой системе координат, кри­ вые подразделяются на алгебраические и трансцендентные. В п. 1.6 было приведено общее уравнение кривой m—vo порядка. В теории плоских алгебраических кривых [16, 29] известны теоремы, опреде­ ляющие общие свойства этих кривых. Приведем основные из них.

1. Порядок алгебраической кривой не зависит от положения этой кривой относительно системы координат. Действительно. Урав­ нения преобразования системы координат, описывающих комбина­

венно старые и новые координаты. Подстановка этих линейных урав­ нений в общее уравнение плоской алгебраической кривой (п. 1.6) не увеличивает и не уменьшает степень этого уравнения.

2. Алгебраическая кривая т-то порядка определяется заданием

m(m + 3)

ее точек. Несложное доказательство этого утверждения представлено в п. 1.6.

3. Две неприводимые алгебраические кривые порядков от, и т2

пересекаются не более чем в от,-от2 точках. Приводимой считается кривая, левая часть уравнения которой может быть представлена в

кривой представляет собой число точек се пересечения с прямой в плоскости кривой.

4. / -кратная точка алгебраической кривой эквивалентна зада-

нию — ~ — - простых ее точек. Помещая начало декартовой системы

координат в t -кратную точку, мы тем самым превращаем общее уравнение кривой (п. 1.6) т-го порядка в уравнение без последних t строк, поскольку только в этом случае t -кратная точка (х - 0,у = 0) будет превращать t раз уравнение кривой в тождество О е О . Оче-

t-(t + l)

видно, количество коэффициентов в этих t строках равно —- • - - .

Применительно к кривой 3-го порядка можно сделать вывод о том, что определяемая девятью простыми точками, она может быть опре­ делена также одной двойной и шестью простыми точками.

рядка. Но поскольку каждая двойная точка первой кривой считается как две точки ее пересечения с другой кривой, то получаем число то-

= т • (т - 2) + ], что противоречит тому, что у кривых порядков т и

(т - 2) число общих точек по теореме 3 равно т-{т-2).

Алгебраические кривые классифицируются не только по их по­

рядку, но и по классу и роду (жанру). Класс алгебраической кривой определяется степенью ее уравнения в тангенциальных координатах.

Пусть линия f(x,у) = 0 пересечена прямой u-x + v-y + \ = 0. Условие

совпадения двух точек ее пересечения с кривой, записанное в виде равенства, связывающего коэффициенты и и V, приводит к уравне­

касания прямой и окружности представляет собой равенство корней

собой тангенциальное уравнение окружности. Геометрически класс плоской кривой определяется числом касательных к кривой линии, проведенных из точки вне кривой. Порядок т и класс к плоской атгебраической кривой в общем случае не совпадают, лишь в случае кривой второго порядка имеет место т = к. Если принять обозначе­ ния: т - порядок кривой, к - класс кривой, d - число двойных то­ чек (узловых и изолированных), г - число точек возврата, t - число двойных касательных (прямых, касающихся кривой в двух точках), w - число точек перегиба, то между этими числовыми характеристика-

134

ми можно установить следующие соотношения, так называемые фор­ мулы Плюккера, полученные им в 1834 году:

к =- т • (т - 1) - 2d - Зг; т = к • (к -1) - 2/ - 3w; w = Зт • (т - 2) - 6d - 8r ; г = Зк • (к - 2) - Ы - 8w.

Род или жанр алгебраической кривой равен числу р, представ­ ляющим собой разность между наибольшим числом двойных точек, которые могут быть у кривой порядка W, и их фактическим числом у данной кривой. Род определяется следующим образом:

Если кривая линия содержит наибольшее число двойных точек, возможных для кривой данного порядка, то она называется рацио­ нальной (кривая нулевого рода). Кривые этого типа обладают сле­ дующим важным свойством: координаты точки, совершающей пере­ мещение по такой кривой, могут быть выражены рациональными функциями некоторого параметра.

Важное теоретическое и практическое значение имеют цирку­

точки: J, (1, /, 0) и J2 (1, - с, 0), где г2 = - 1 . Очевидно, координаты этих точек не зависят от коэффициентов в уравнении окружности. Поэто­ му можно ут верждать, что любая окружность в плоскости пересекает ее несобственную прямую в двух мнимых точках, которые назы­ ваются циклическими. Алгебраические кривые, проходящие через циклические точки, называются циркулярными. К циркулярным

Следовательно, кривая Бурместера является циркулярной кривой. По­ скольку она третьего порядка, то в пересечении с окружностью обра­ зует шесть точек, из которых две точки - циклические, а четыре точки - вещественные. Кривые второго порядка могут быть получены цен­ тральным проецированием окружности на соответствующую каждой кривой плоскость. Центральным проецированием определенного се­ мейства циркулярных кривых m - го порядка на плоскость также можно получить любую кривую т-го порядка. Рациональные цирку­ лярные кривые нашли множественные практические применения. Папример, кривая Бурместера - в теории синтеза плоских механизмов, лемниската Бернулли - в профилировании лопаток турбин, теорети­ ческие профили Жуковского, Чаплыгина в авиастроении и др.

В завершении обзора способов образования плоских кривых от­ метим, что мир этих кривых бесконечно велик [29]. Гак, например, известно более 70 видов алгебраических кривых третьего порядка. Классификация кривых четвертого порядка связана с именем Варинга (1792 г.) и насчитывает 84551 кривых частных видов. Алгебраические кривые более высоких порядков изучены недостаточно и не имеют сколь-нибудь законченной их классификации. Многообразие плоских трансцендентных кривых также велико [29], но оно менее изучено в геометрии, по сравнению с алгебраическими кривыми, ввиду сложно­ сти их геометрической природы. Если исследования метрических свойств (кривизна, квадратура, спрямление) у трансцендентных кри­ вых выполнены достаточно основательно, то, например, проективные свойства этих линий не изучены. Нет достаточно удовлетворительной классификации трансцендентных кривых линий.

5.1.6.Кинематическая геометрия плоских кривых

Рассмотрим подробнее упомянутый ранее кинематический спо­ соб образования плоских кривых. В основу одного из применяемых в начертательной геометрии методов преобразований - метода плоско­ параллельного перемещения, положено предложение о том, что вся­ кое перемещение плоской фигуры в ее плоскости из одного конечного положения в другое конечное положение может быть достигнуто по­ воротом фигуры относительно некоторого центра в этой плоскости. Это предложение имеет место и для бесконечно малого перемещения плоской фигуры в ее плоскости. В этом случае траекторией любой точки плоской фигуры является бесконечно малая дуга окружности и с точностью первого порядка малости бесконечно малое перемещение этой точки может быть заменено перемещением по касательной к бесконечно малой дуге, а перпендикуляр к касательной в этой точке занимает положение нормали. Точка пересечения подобных норма­ лей, каждая их которых определяется траекторией мгновенного пере­ мещения соответствующей точки плоской фигуры при ее мгновенном плоскопараллельном перемещении, является мгновенным центром вращения плоской фигуры. Множество мгновенных центров враще­ ния плоской фигуры в неподвижной декартовой системе координат в плоскости фигуры представляет собой кривую - неподвижную цен­ троиду движения плоской фигуры. Множество мгновенных центров вращения в подвижной системе декартовых координат, неизменно связанной с подвижной плоской фигурой, представляет собой под­ вижную центроиду. Точка, неизменно связанная с фигурой, совер­ шающей непрерывное плоскопараллельное перемещение, описывает некоторую плоскую кривую. Эту кривую можно рассматривать также как образованную той же точкой, неизменно связанной с подвижной центроидой, при качении без скольжения последней по неподвижной центроиде. Кривые описанной кинематической схемы образования называются рулеттами [2, 8].

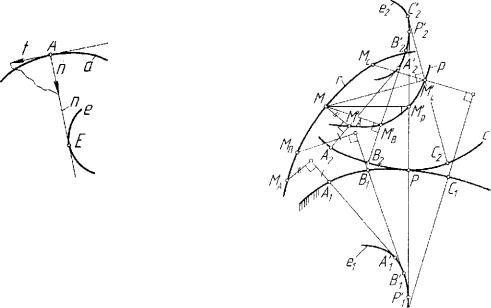
В свете сказанного рассмотрим в качестве примера кинематиче­ ское образование эволюты плоской кривой (рис. 5.17). В каждой обыкновенной точке А кривой а су­ ществует репер Френе, образованный

единичными векторами касательной t и нормали п. Рассматривая репер как плоскую фигуру, совершающую не­ прерывное плоскопараллельнос пере­ мещение при движении его вершины

Авдоль линии а, на основании вы­

кривой О.. Следовательно, неподвижной центроидой непрерывного плоскопараллельного перемещения репера кривой служит ее эволюта. Очевидно, подвижной центроидой движения репера служит нормаль­ ная прямая п. В таком случае кривая линия а представляет собой траекторию движения точки А, неизменно принадлежащей прямой линии т?, когда, последняя обкатывает кривую е, то есть линия а есть рулетта точки А, принадлежащей подвижной центроиде п, обкаты­ вающей неподвижную центроиду е. Это как раз соответствует ранее изложенному кинематическому образованию эвольвенты а по ее эволюте е.

Рассмотрим образование рулетты. Для получения рулетты необ­

ходимо, как следует из вышесказанного, задать неподвижную цен­

троиду сх, подвижную центроиду с2 и точку М, образующую рулет-

ту. Точка М неизменно связана с подвижной центроидой с2

(рис. 5.18). Центроиду сх представим как дискретный ряд точек

Ах, Вх, Р,СХ,..., которому отвечает по условию равенства длин соот­

ные от точки М до оснований построенных перпендикуляров к нор­ малям центроиды с2. Множество полученных точек принадлежит ру-

летте г. Очевидно, по характеру построения рулетга г принадлежит неподвижной плоскости центроиды с{.

Рассмотрим теперь вопрос определения кривизны рулетты. Пусть