1671

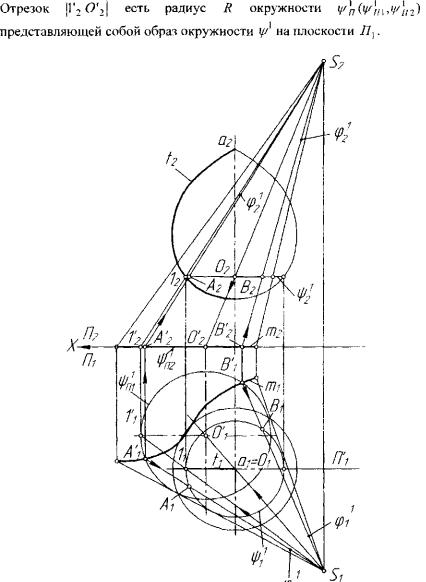
Рис. 7.26. Пример определения точек линии пересечения поверхности вращения и конической

отображении будет непрерывное однопараметрическое множество окружностей с центрами на прямой 5, ах.

Если заданные поверхности & и Q поменять "ролями" в алгоритме 7.2, то есть принять нормальную циклическую конгруэнцию Ч*2^ =\Ji//1, индуцируемую поверхностью вращения

2

Q(a,t), в качестве фактормножества пространства Ei, то получим неудачный выбор инструмента для решения рассматриваемой задачи, поскольку каждая образующая (р1 поверхности 0 будет отображаться на плоскость отображения П'П П2, IFzoa в гиперболу.

Рассмотрим пример применения в алгоритме 7.2 проецирующего нелинейного фактормножества пространства преставляющего собой нормальную циклическую конгруэнцию Ф2{1) ={J<p]. Опрсде-

лим несколько точек линии пересечения двух поверхностей вращения ©(bji) и Q(a,m) с параллельными осями а и Ь и образующими - кривыми линиями тип (рис. 7.27). Последовательность алгоритми­ ческих действий и конструктивных построений может быть нижеследующей:

1. Поверхность вращения 0{b,ri) представляем как непрерывное

отображении будет ее фронтальный очерк, составляющей линией которого является линия n(nu>h).

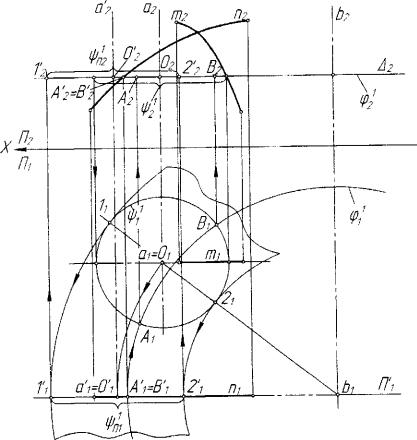
Рис. 7.27. Пример определения точек линии пересечения двух поверхностей врао1ения

фронтальные проекции образов А' и В' искомых точек А и В, принадлежащих линии пересечения поверхностей 0 и Q, а затем

известный в начертательной геометрии способ вспомогательных плоскостей (плоскостной посредник) [2, 15, 20, 22], истинное происхождение которого обосновано логикой алгоритма 7.2, построенного на основе теоретико-множественного анализа образова­ ния множества пересечения.

Рассмотрим случай пересечения, который отличается от

Определим несколько точек линии пересечения поверхностей на основе алгоритма 7.2. Для этих целей примем одну из поверхностей, например 0, в качестве индуцирующей фактормножество про­ странства £ 3 . В таком случае получаем нижеследующую последо­ вательность построения точек линии пересечения.

1. Поверхность вращения 0{J,b) представляем как непрерывное однопараметрическое множество окружностей <рх в плоскостях, пер­

2

3.Плоскость П'Н П2, n'(iC\j) принимаем в качестве плоскости отображения. Образом поверхности 0 в принятом отображении будет

еефронтальный очерк, составляющей линией которого является заданная образующая линия b(bub2).

4.Поверхность вращения Q(i,a) рассматриваем как непрерыв­ ное однопараметрическое множество Wxxx)-\Jy/x окружностей ц? в

плоскостях, перпендикулярных оси /(/,,/2).

5.На плоскости ТТ строим отображение w\i(>P~\n>Wn7) одной из линий - окружностей ц/х(у/\,y/\) поверхности Q. Образованию об­ раза у/1п линии у/1 можно дать следующее геометрическое обосно­ вание. Окружность Ц ' Х п р и вращении относительно оси /

большую окружность у'/(y//7i,<//}/2)> которая и является образом выбранной окружности у/ на поверхности Q.

6. Определяем точки А'2 и В'2 - фронтальные проекции образов А" и В' точек А и В, принадлежащих линии пересечения поверхностей О и Q. Горизонтальные проекции этих образов принадлежат следу П\ плоскости отображения 77. Поскольку образы А' и В' и соответствующие им прообразы А и В, принадлежат одной

окружности (рх((р\,(р\) проецирующей нормальной циклической конгруэнции, то в пересечении линий <р1 и у/1 определяем прообразы

- точки А(А),А2) и В(ВиВ2) линии пересечения поверхностей. Очевидно, образом поверхности Q{i,a) в рассматриваемом отображении будет пучок Qn =U^j? концентрических окружностей с центром 0(0{,02).

Проанализируем выполненные построения. Переход от точек - образов А' и В' к их прообразам А и В происходит по окружности

Рис. 7.28. Пример определения точек линии пересечения двух поверхностей вращения

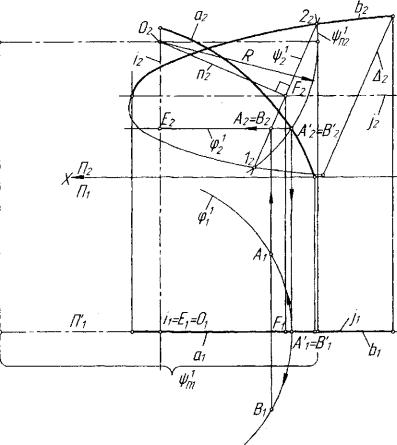
q>\(p\,(p\), принадлежащей сфере радиуса R. Этой же сфере принад­ лежат линия - прообраз у/^(ц/\и соответствующий ей образ

У/п(Ч/п\^пт)- В э т о и св язи описанные построения могут быть упро­ щены, если не выполнять промежуточные построения образов А'.В1. Выбор промежуточной сферы R сразу приводит к ее окружностям срх и у/1 пересечения с поверхностями 0 и Q соответственно, а точки пе­ ресечения А и В определяются как общие точки этих окружностей: (Л,В) = <р1С)у/] . Это соответствует известному в начертательной гео­ метрии способ концентрических сфер [2, 15, 20, 22], происхождение и обоснование которого также следует из логики алгоритма 7.2.

Рассмотрим еще один пример применения алгоритма 7.2, кото­ рый дает объяснение происхождению еще одного известного в начер­ тательной геометрии способа построения линии пересечения двух по­ верхностей. Определим несколько точек линии пересечения поверх­

образующих окружностей, А - плоскость параишлизма (рис. 7.29). В соответствии с логикой алгоритма 7.2 может быть предложена ниже­ следующая последовательность определения точек линии пересече­ ния заданных поверхностей.

1. Поверхность вращения 0{i,a) представляем как множество окружностей <р{ в плоскостях, перпендикулярных оси / поверхности:

отображения. Образом поверхности 0 в принятом отображении будет

еефронтальный очерк, в состав которого входит заданная

плоскости параллелизма А, с центром на оси j.

5. Строим на плоскости И образ Wn^m^ni)^ полученный

Рис. 7.29. Пример определения точек линии пересечения поверхности вращения и циклической

проведенный из ее центра F(FY , F2 ), 1 и 2 - диаметрально противо­ положные точки окружности у/1. Эта сфера пересекает плоскость от­ ображения /7, которой принадлежит центр сферы, по большой ок­ ружности У л О / ш ^ л г ) ' которая и является образом выбранной окружности у/х на поверхности Q.

6. Определяем точки (А'2 - В'2 ) = а2Г\Ул2 ~ фронтальные проекции образов А' и В' точек А и В линии пересечения

риваемом отображении будет непрерывное однопараметрическое

происхождение и обоснование которого следует из логики алгоритма 7.2.

З А К Л Ю Ч Е Н И Е

Начертательная геометрия должна рассматриваться в первую очередь как раздел математики, изучающий теорию и методы конст­ руктивных отображений пространств различных размерностей и структур друг на друга. В частности пространств высших размерно­ стей с нелинейными структурами на пространства низших размерно­ стей с линейной структурой. Только во вторую очередь она может быть трактована узко специализированно как теоретическая основа построения чертежей пространственных фигур на плоскости.

Основываясь на этой точке зрения, начертательную геометрию не имеет смысла делить на геометрию трехмерного пространства и гео­ метрию многомерного пространства, упуская из вида начертательную геометрию двумерного пространства (теорию графических построе­ ний на плоскости или поверхности). Ьолее перспективным в научном плане будет деление начертательной геометрии на геометрию линей­ ных конечномерных пространств и нелинейную начертательную гео­ метрию, начертательную геометрию евклидова пространства и неевк­ лидову начертательную геометрию. Основы создания таких разделов уже заложены: нелинейная начертательная геометрия может начи­ наться с конструктивной теории инверсии, квадратичных преобразо­ ваний, конструктивной теории проективного формообразования кри­ вы, поверхностей и алгебраических многообразий высших размерно­ стей, изучением их свойств посредством отображения на другие мно­ гообразия.

На этом пути развития начертательной геометрии, как математи­ ческой науки, могут проявиться её связи не только с линейной алгеб­ рой и алгебраической геометрией, но и с другими важными разделами математики, такими как теория функций комплексных переменных, дифференциальная геометрия, интегральная геометрия, топология.

Настоящий учебник не преследует таких целей - это дело буду­ щего. Однако в нем сделана попытка ввести элементы многомерной начертательной геометрии, элементы исчислительной геометрии и показать тесную связь с дифференциальной геометрией кривых. Этот учебник не предназначен для первого чтения. Чтобы усвоить предла­ гаемый материал, требуется знакомство с традиционным курсом на­ чертательной геометрии, аналитической и дифференциальной геомет­ рии в объеме курсов высшей школы.

Владимир Яковлевич Волков, Виктор Юрьевич Юрков, Константин Леонидович Панчук, Наталья Викторовна Кайгородцева

КУРС НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ НА ОСНОВЕ ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ

Учебник

Редактор - Константин Леонидович Папчу к

Подписано к печати 29.10.2010 Формат 60x90 1/16. Бумага офсет пая 80 гр/м2

Оперативный способ печати Гарнитура Times New Roman Усл. п. л. 15.8

Тираж 300 экз. Заказ № 2512 11ена договорная

Издательство СибАДИ 644099, г. Омск, ул.П.Некрасова, 10

Отпечатано в издательстве ООО «Полиграфист» 644116, г. Омск, ул. Герцена, 268