1671

Аналогично можно записать уравнение множества пучков пря­

И так далее.

В качестве примере рассмотрим получение уравнения линейча­ той поверхности, заданной условиями А2 • Аг • В3 (табл. 6.1). Пусть ус­

— — — + г2 = Ь1. Это есть уравнение искомой поверхности, записан-

{.У-а?

нее в неявном виде. (Рекомендуется построить чертеж поверхности самостоятельно). Следует заметить, что это не единственный способ получения уравнения этой поверхности.

Рассмотрим пример вывода уравнения циклической поверхности, заданной условиями Аъ-В2. Пусть условие Аг обеспечивается тем, что центр окружности принадлежит винтовой линии, а условие В2 обеспечивается постоянным углом наклона плоскости окружности к данной винтовой линии. Пусть окружность имеет постоянный радиус. Нетрудно подметить, что суммарная размерность условий равна че­ тырем. Учитывая, что множество окружностей постоянного радиуса

200

имеет размерность, равную пяти, получим однопараметрическое не­

х — г • c o s a + R • cos<5,

у= г - sin яг + R - sin <5 ,

2 = р • S .

Если у = 90°, /3-0°, то плоскостью параллелизма будет плос­ кость OXZ. Если 0 < у < 90°, /? = 0°, то будет существовать поверх­ ность параллелизма - прямой круговой конус с осью OZ. (Чертежи всех этих поверхностей рекомендуется выполнить самостоятельно).

Если центр образующей располагается на конической винтовой линии

x = a-S-cosS, у = а • 8 • sin S , z = р • S ,

а плоскостью параллелизма будет плоскость OXY, то уравнения по­ верхности будут иметь следующий вид

х = г • c o s e r + г + а • 8 • соъё,

у = г • sin а + а - 8 • sin 8 , z = P-S.

Вывод этих уравнений полностью анаюгичен.

201

ГЛАВА 7. КОНСТРУКТИВНОЕ ОПРЕДЕЛЕНИЕ МНОЖЕСТВА ПЕРЕСЕЧЕНИЯ

Одной из основных тем учебного курса начертательной геомет­ рии является тема "Позиционные задачи". К позиционным относятся задачи на определение взаимной принадлежности и взаимного пере­ сечения геометрических объектов в евклидовом пространстве. Из­ вестное в существующих учебниках традиционное изложение этой темы предусматривает использование нескольких узкоспециализиро­ ванных методов решений задач на пересечение.

Рассмотрим построения различных алгоритмов решений позици­ онных задач, исходя из теоретико-множественных представлений множества пересечения двух множеств в евклидовом пространстве.

7Л. Алгоритмы конструктивного определения множества пересечения

Формула (1.7) позволяет определить размерность множества пе­ ресечения двух линейных множеств: т- плоскости и q - плоскости в пространстве Е<;. Покажем, что эта формула справедлива и для двух нелинейных множеств этого пространства. Пусть в пространстве Е„ находятся два пересекающихся линейных множества А""и У. Их общая часть - линейное множество пересечения Zp имеет размер­ ность, определяемую формулой (1.7): р = m + q-n. Введем в про­ странстве Еп нелинейное преобразование F, описываемое уравне­ ниями:

применения преобразования F линейному множеству Хт будет со­ ответствовать некоторый нелинейный образ. В силу непрерывности

функций /,,/,, ... ,/„ две достаточно близкие точки множества Хт

202

перейдут в две сколь угодно близкие точки, принадлежащие образу пого множества, то есть непрерывность в расположении точек явля­ ется инвариантом преобразования F. В силу взаимной однозначности

преобразования любой точке множества Хт будет соответствовать единственная точка - образ на образе множества Хт, то есть количе­ ство независимых параметров, определяющих положение точки - образа и точки-прообраза в фиксированной системе координат про­ странства Е„ будет одно и то же - т. Таким образом, количество т независимых параметров и их непрерывность являются инвариантами нелинейного преобразования F, что позволяет сделать вывод об ин­ вариантности размерности линейного множества Хт и других линей­ ных множеств пространства Еп относительно этого преобразования.

При использовании формулы размерности (1.7) множества пере­ сечения необходимо учитывать нижеследующее.

2.Формула справедлива для множеств Хт и Y4 общего поло­

1.m = q = 2, откуда следует р = 1, что указывает на то, что мно­

ставления каждого из этих множеств в виде фактормножества по от­ ношению эквивалентности, представляющем собой разбиение на не­ пересекающиеся классы, определенном на каждом из множеств X2 и

1.« т 2 П А ' 2 = ^ ' ;

2. o-2f]Y2 =^';

3 . ^ W = z ° .

Поскольку множество Z1*-0-1 = {Jz(} есть непрерывное однопараметрическое множество точек, то есть линия, то для ее определения необходимо непрерывное однопараметрическое применение приве­ денного алгоритма. Таким образом, однопараметрическому точечно­ му множеству \Jz° =Z 1 ( 0 ) взаимно однозначно соответствует однопа­ раметрическое множество \J<72 — Х^2) плоскостей или поверхностей. Представлял множество 271<2) = {Ja2 как фактормножество множества (пространства) Еъ по отношению эквивалентности, представляющем собой разбиение пространства £3 на однопараметрическое множест­ во непересекающихся классов а2 (плоскостей или поверхностей),

204

можно получить общий алгоритм конструктивного определения мно­ жества Z1(0) пересечения двух множеств X2 и Y2 пространства Еъ.

Алгоритм 7.1

1. £ 3 = 2 - 1 ( Ц =Ua2 =>ljff?,/ = l,2,...,*r;

2.а2(\Х2=(р)',

3.aff)Y2 = у/];

4.<р)Г\¥]=г*;

5.U4'=>Uz°=Z,(0>.

При конструктивной реализации алгоритма непрерывное однопа­

множественного рассмотрения пересечения двух множеств в про­ странстве £ 3 , соответствует известному в начертательной геометрии методу посредников, к которым относятся вспомогательные плоскостн и поверхности [2, 15, 20, 22].

разбиение этого пространства на классы эквивалентности, может быть положено разбиение одного из пересекающихся множеств X2 и Y на непересекающиеся классы, например X2 - Ф в д , с последую-

205

щим расширением множества полученных классов до проецирующе­ го фактормножества Ф2(1), то есть X2 = Фт -> Ф20) = Е3. На основа­

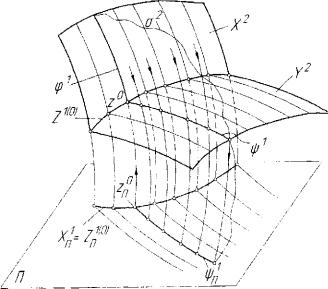
нии сказанного может быть предложен нижеследующий алгоритм конструктивного определения множества пересечения Zw> двух множеств X2 и Y2 (рис. 7.1).

Рис. 7.1. Интерпретация алгоритма 7.2

Алгоритм 7.2

1. х2 = Фт = t V ;

2 . ф Н 1 ) _ > ф 2 ( 1 ) = и ^ = £ з .

2

3.г2 =vK1) = иУ;

4.Вводится П - плоскость проекций (плоскость сюръективного

одновременно проекция искомой линии Z ,

206

6. IV->!>}/;

8 . z ^ z » 6 ^ , U z ° = Z 1 ( 0 ) .

Отображение множества У" на плоскость // в п.6, выполняемое проецирующим фактормножеством Еъ = Ф2<" = \J<px, в общем случае,

в соответствии с логикой алгоритма 7.2, должно быть биективным. Рассмотренный алгоритм по существу сводится к алгоритму 7.1. Дей­ ствительно. Классы-линии <рх и у/х в алгоритме 7.2 принадлежит не­ которому множеству а2 (плоскость или поверхность), на котором ос­ новано построение алгоритма 7.1. Представление исходных пересе­ кающихся множеств в виде объединения непересекающихся классов X2 = []<рх и Y2 = [)у/х, пары которых принадлежат одному множест­ ву, то есть (фХ ,у/х) а а2, приводит к образованию непрерывного однопараметрического множества двумерных классов U а2 , образую-

ства Е3 - Ф2{Х> с последующим использованием его в качестве про­ ецирующего для отображения пространства на плоскость, в отличие от алгоритма 7.1, в котором выбор фактормножества Еу = 271(2) никак не оговорен. Очевидно, построение различных фактормножеств про­ странства £3 по отношению эквивалентности, представляющим со­ бой разбиение множества на классы, зависит как от геометрической формы пересекающихся множеств X7, Y2, так и от самого отноше­ ния эквивалентности, которое в частности может быть разбиением пространства £\ на непересекающиеся проецирующие классы. Прак­ тическая целесообразность того или иного алгоритма конструктивно­ го определения множества пересечения зависит от возможности дос­ тижения минимальной сложности геометрической формы тех проме­ жуточных элементов и классов элементов, которые участвуют в алго­ ритме.

207

Рассмотрим теперь второй случай, когда от = 1, q-2, р = 0. Как было отмечено выше, множество пересечения Zp в этом случае пред­ ставляет собой точку или конечное число точек и может быть полу­ чено, если оба множества Xх и Y2 линейны {X1 - прямая, F 2 - плос­ кость); оба множества Xх и Y2 нелинейны (X1 - кривая линия, Y2- поверхность); одно из множеств, например Х\ линейно (прямая), а другое - Y2 - нелинейно (поверхность), либо А'1, нелинейно (кривая линия), а У2— линейно (плоскость). Поскольку q~2, то точечное

то в возможных алгоритмах конструктивного определения множества

пересечения должно присутствовать множество 2 .

Рассмотрим алгоритм конструктивного определения множества пересечения X1П Y".

Алгоритм 7.3 (рис. 7.2)

=272(|) =и<?1 ~ проецирующее фактормножество (двухпара-

2

метрическое множество проецирующих классов - линий а]);

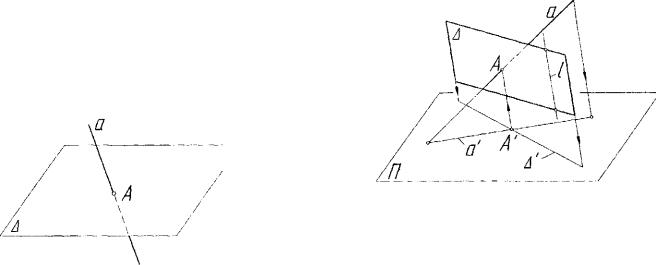
Рис. 7.2. Интерпретация алгоритма 7.3

1. Xх -» Х\, (Xх, Ху) с: \Jcrl - проецирующая поверхность; 2. ХХС\Х\ = Z° .

Очевидно, в этом алгоритме проецирующее отображение Л'1 —> Хху является биективным с инвариантной точкой Z 0 , которая является искомой.

Алгоритм 7.4 (рис. 7.3)

1. r2=r,(1)=iV;

2

3.Вводится /7 - плоскость проекций (плоскость сюръектинного отображения пространства £ ' 3 );

4.X1 -> .A"J7 (биективное отображение);

5.Г2 —> Уя (след проецирующего множества К2 );

6 . A - ' , r i ^ = Z & ;

7.Z*j^Z°eX\

Запись в п.2 алгоритма означает, что фактормножество У" = 4/Xtl) индуцирует в пространстве £, проецирующее фактормножество

У2(1) -\Ji//x = э т о г о пространства. Как и в случае рассмотренных

Рис. 7.3. Интерпретация алгоритма 7.4

алгоритмов конструктивного определения множества пересечения

же основным критерием практической целесообразности алгоритма является достижение минимальной сложности геометрических форм классов эквивалентности, объединение которых является фактормно­ жеством пространства Е3, и в целом - достижение минимальной сложности всех этапов конструктивной реализации алгоритма.

Впоследующем изложении настоящей главы будут рассмотрены примеры практических реализаций вышеприведенных алгоритмов конструктивного определения множества пересечения.

7.2.Алгоритмы конструктивного определения множества пересечения двух линейных множеств

Вглаве 4 были приведены традиционные решения задач опреде­ ления пересечения прямой и плоскости и двух плоскостей. Рассмот­ рим взаимосвязь приведенных решений и предложенных алгоритмов,

атакже иные решения названных задач, основанные на этих алгорит­ мах.

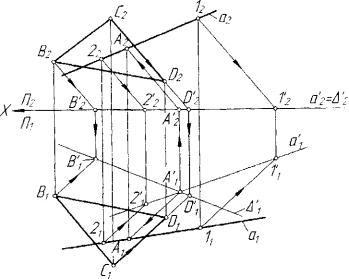
Рассмотрим вначале за­ дачу о пересечении прямой и плоскости. Проведем ана­ лиз возможных подходов к решению этой задачи с по­ зиций теоретических по­ строений, положенных в основу предложенных алго­ ритмов. Поскольку прямая а и плоскость А (рис. 7.4)

являются линейными мно- рис. 7.4. Пересечение прямой и плоскости жествами, то возможные фактормножества пространства Е3, используемые в алгоритмах 7.3 и

7.4, также должны быть линейными, то есть линейными должны быть как множество классов эквивалентности, гак и сами классы эквива­ лентности.

210

В этой связи фактормножество в алгоритме 7.3, то есть

Еъ = 2''(1) = U с ' . должно быть проецирующей конгруэнцией Кг (1,0),

2

то есть связкой с собственным или несобственным центром. Посколь­ ку решение задачи выполняется на графической модели пространства Еу, представляющей собой чертеж Монжа, то в качестве проеци­ рующей связки может быть выбрана связка с несобственным центром, прямые которой перпендикулярны плоскости проекций Я, или 77,. На рисунке 4.1 приведен пример конструктивного определения точки пересечения прямой с и плоскости (alib), в котором используется связка, проецирующая относительно 772. При этом роль проецирую­ щей поверхности \Jal в алгоритме (рис. 7.2) играет проецирующая плоскость (cC\d), где с - исходная прямая, d - ее образ на исходной плоскости (alib) в отображении, выполняемом проецирующей связ­ кой.

кости 77, относительно оси х до совмещения с плоскостью П2. В этом преобразовании полю точек 77, соответствует поле точек 772. Если этими двумя проецирующими связками отображается на плос­ кости 77, и Т12 некоторое двухпараметрическое множество точек про­ странства Е2 — линейное (плоскость) или нелинейное (поверхность), то возникает преобразование совмещенной плоскости Я, = П2, ли­ нейное — в случае задания плоскости и нелинейное — в случае задания поверхности. Линейное преобразование - родство, является моделью

2X1

плоскости пространства и может быть использовано для решения рас­ сматриваемой задачи. Пример этого решения приведен на рисунке 4.8. Оба отмеченных решения, первое из которых - прямо, а второе - косвенно, связаны с алгоритмом 7.3.

Рассмотрим использование алгоритма 7.4 для решения задачи оп­ ределения точки пересечения прямой а и плоскости А (рис. 7.5). В

2

ритме 7.4. Последовательность решения рассматриваемой задачи в соответствии с алгоритмом 7.4 и с учетом принятых обозначений мо­ жет иметь нижеследующий вид.

3.Определяется образ искомой точки пересечения: А'- а'Г\А'.

4.Определяется прообраз - искомая точка: Л'—> А е а. Рассмотрим примеры реализации этого алгоритма на графической модели пространства Щ. Пусть на модели заданы: прямая а, плос­ кость A(SBCD) (рис. 7.6). Требуется определить точку пересечения оГ]А. Для решения задачи назначим в качестве прямой I с: А сторону

Рассмотрим решение еще одной задачи, в условии которой зада­ ны плоскость A(ff)h), прямая а и требуется также определить точку пересечения аГ]А (рис. 7.7). Для решения задачи выберем отображе­ ние пространства Еъ на плоскость П = П2 при помощи проецирую­

приведенных решения (рис. 7.6 и 7.7) соответствуют известному в на­ чертательной геометрии способу вспомогательною проецирования [21].

Рис. 7.6. Пример определения пересечения прямой и плоскости

Рассмотрим еще одно решение рассматриваемой задачи, отли- ,ч чающееся от предыдущих выбором проецирующей связки. Для опре-

деления точки пересечения аГ\А выберем в качестве проецирующей связку (а), определяемую самой прямой а, и плоскость отображения П (рис. 7.8). Алгоритм решения задачи в этом случае может иметь нижеследующий вид.

1. Определяется образ dczTI прямой а в отображении, выпол­ няемом связкой (а).

2. Задается точка В е А и строится ее образ В'. Пара точек А' и В' определяют образ Ь' некоторой вспомогательной прямой bczA,

4.Две точки М = Ь'Г\А' и В в А определяют прообраз - вспо­ могательную прямую Ь .

5.Определяется искомая точка пересечения А = ЬГ]а.

Рис. 7.7. Пример определения пересечения прямой и плоскости

На рисунке 7.9 в соответствии с этим алгоритмом приведено ре­

сти отображения принята плоскость П = /72. Последовательность по­ строений в этом решении может иметь нижеследующий вид.

/2 = Ат — фронтальный след плоскости А .

5.Пара точек М и В определяют прообраз - вспомогательную

возникает задача о пересечении двух плоскостей. Ранее в п. 4.2 было приведено ее решение (рис. 4.6), основанное на задании двух прямых в одной плоскости и определении точек пересечения этих прямых с другой плоскостью. Это решение, выполненное на графической моде­ ли пространства по существу соответствует двукратному приме­ нению алгоритма 7.3, позволяющему определить точку пересечения прямой и плоскости.

Как было показано в п. 4.2, задание на графической модели про­

чи построения линии пересечения этих плоскостей к решению задачи

Рис.7.8. Интерпретация алгоритма 7.4

определения общей прямой двух родственных преобразований. Такой подход реализован на рисунке 4.8.

Анализ вышерассмотренных решений задач на пересечение пока­ зывает, что существуют варианты решений одной и той же задачи, среди которых есть более простые (рис. 4.1) и более сложные (рис. 7.6) в конструктивной реализации варианты. Многообразие ва­ риантов следует из тех теоретико-множественных построений, кото­ рые были положены в основу предложенных алгоритмов конструк­ тивного определения множества пересечения. Эти алгоритмы не ис­ черпывают возможности теоретико-множественного подхода в этом направлении его применения. Рассмотренные решения задач, осно­ ванные на применении отображения, указывают на возможность по­ строения алгоритмов с использованием преобразования, как частного случая отображения, например, родства (см. гл. 4).

Рис. 7.9. Пример определения пересечения прямой и плоскости

7.3. Алгоритмы конструктивного определения множества пересечения двух множеств, одно из которых

двумерно и нелинейно

Указанному в заголовке названию соответствуют решения задач определения линии пересечения плоскости и поверхности, а также

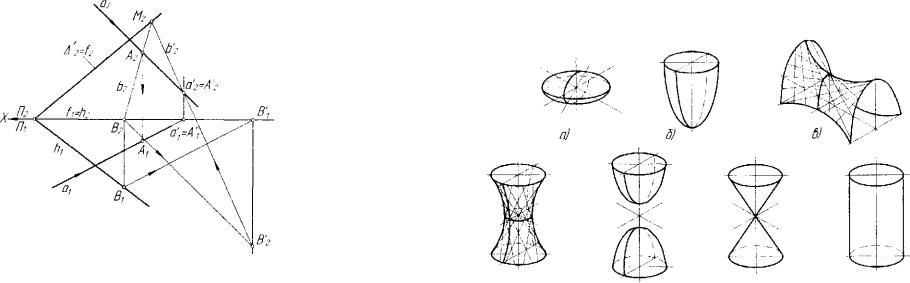
точек пересечения линии (прямой или кривой) и поверхности. Сле­ дующими после плоскости наиболее изученными и часто используе­ мыми в практических приложениях следуют поверхности второго по­ рядка (квадрики). Множества невырожденных, то есть нераспавшихся па две плоскости, квадрик включает (рис. 7.10): а) эллипсоиды (об­ щий - трехосный и вращения - сжатый или вытянутый при вращении эллипса относительно малой или большой его оси соответственно); б) параболоиды эллиптический и вращения; в) параболоид гиперболиче­ ский; г) одноиолостные гиперболоиды эллиптический и вращения; д) двухполостные гиперболоиды эллиптический и вращения; е) прямые конусы эллиптический и вращения и наклонные конусы эллиптиче­ ский и круговой (в качестве направляющей линии конуса может быть взята любая нераспавшаяся кривая второго порядка); ж) прямые ци­ линдры эллиптический и вращения и наклонные цилиндры эллипти­ ческий и круговой (направляющей линией цилиндра также может быть любая нераспавшаяся кривая второго порядка). Квадрики на ри­ сунке 7.10 (в, г, е, ж) - линейчатые поверхности.

Рис. 7.10. Поверхности второго порядка

Рассмотрим возможные алгоритмы конструктивного определения линии пересечении квадрики и плоскости, а также точек пересечения линии, в частности прямой, с квадрикой. В соответствии с принятыми в п.п. 7.1 и 7.2 теоретико-множественным подходом к определения

множества пересечения в пространстве е3, необходимо это простран­

ство представить в виде проецирующего фактормножества Е~ = Ф2<1> = [}<рх. Как было отмечено ранее, основным критерием вы-

2

бора фактормножества Ф2(1) ={J<px является минимальная сложность

2

геометрической формы класса <рх эквивалентности (проецирующего

класса) и минимальная сложность самого множества [}<р1 этих клас-

2

сов. В рассматриваемой задаче о пересечении с участием квадрики на выбор фактормножества пространства /5, будет, несомненно, влиять геометрия конкретной квадрики, которая определяет аффинные, мет­ рические и проективные свойства этой поверхности. В современной начертательной геометрии известны результаты исследований ука­ занных свойств квадрик. Множество этих результатов включает тео­ ремы и предложения, которые характерны для всех перечисленных невырожденных квадрик и достаточно полно раскрывает их свойства [13, 32]. Приведем эти свойства, поскольку они потребуются для раз­ работки последующих алгоритмов.

1.Пучок плоскостей, проходящий через ось квадрики, рассекает

еепо семейству кривых второго порядка, родственных между собой.

2.Два произвольных эллиптических сечения квадрики всегда перспективны.

3.Параллельные между собой плоскости могут пересекать квад­ рику по подобным и подобно расположенным эллипсам.

4.Любое коническое сечение квадрики и окружность, или лю­ бые два конических сечения квадрики, могут быть приведены в пер­ спективное соответствие с помощью конической поверхности второго порядка двумя различными способами.

5.Любые сечения конуса второго порядка плоскостями, не про­ ходящими через вершину, перспективны с центром перспективности

ввершине конуса.

6.Стереографическая проекция из омбилической точки квадри­ ки ее произвольного плоского сечения на соответствующую этой точ­ ке плоскость круговых сечений есть окружность.

Рассмотрим вначале примеры определения линии пересечения квадрики и плоскости. Пусть на графической модели пространства заданы фронтальное и горизонтальное изображения отсека эллипти­ ческого однополостного гиперболоида Г и след Р2 плоскости Р А.П2

218

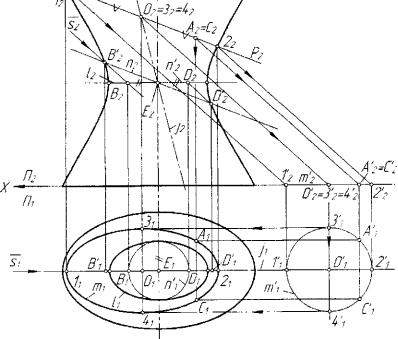
(рис. 7.11). Требуется построить линию пересечения РГ\Г. Для ре­ шения задачи воспользуемся свойством 3 квадрики. Пучок плос-

П72 '

Рис. 7.11. Пример определения пересечения квадрики и плоскости

костей, параллельных плоскости Р, рассекает поверхность Г по по­ добным и подобно расположенным эллипсам с центрами на прямой _/'(/)) / 2 ) . По эллипсу в плоскости Р определяем направление s(si,s2) проецирующей связки с несобственным центром, принимаемой в ка­ честве фактормножества == Ф2(1>, и выбираем в качестве плоскости отображения плоскость П = Л, . Направление J определяется сле­ дующим образом: в горловой эллипс l(lx,l2) поверхности Г вписыва­ ется окружность n'(n\,n'2), диаметр SD(S,D,,/i2D2) которой равен длине малой оси этого эллипса; линия п2ПР2 отсекает на фронталь­ ном очерке поверхности Г точки В'2 и D'2; B\D\ есть фронтальное

219