
1671
.pdf
соответственно в е Я , ; С е /72; D <= /73 (рис. 3.4). В случае равенства нулю двух координат точки получаем ее принадлежность оси проек
ции, например, точка |
Е(х, О,0) е X . |
|
|
|
|
||||||||
Точно также можно построить проекции точки |
А |
общего положе |
|||||||||||
ния |
на плоскости |
X хТ, YxT, |
Z хТ |
модели четырехмерного |
про |
||||||||
странства |
(рис. |
3.5). |
Здесь |
А4 |
е X хТ, |
АЪ е Y хТ, |
А6 |
<а Z хТ . |
Бели |
||||
одна из координат равна |
|
|
|
IT |
|
|
|||||||
нулю, |
то точка |
принад |
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||||
лежит |
гиперплоскости |
|
|
|
|
|
|
||||||
координат. |
Если |
какие- |
|
|
|
|
-Л As |
|
|||||
либо |
|
две |
координаты |
|
|
|
|
|
|
||||
равны |
нулю, |
то |
точка |
|
А? |
|
|
-\j^A6 |
|
||||
принадлежит |
плоскости |
|
|
|
|
||||||||
П2Д |
|
|
|
|
|||||||||
проекций. Если три ко X- |
|
О |
4 _ L _ |
|
|||||||||
/7; |
|
|
|
Y.T |
|||||||||
ординаты |
равны |
пулю, |
|
|
|
|
|
||||||
то |
точка |
принадлежит |
|
At |
|
|
|
|
|||||
оси |
координат. |
Напри |
|
|
|
|
|
||||||
|
|
|
Y |
|
|
||||||||
мер, |
|
В(х, |
у, |
0, |
0 |
при |
|
|
|
|
|
||
надлежит |
гиперплоско |
Рис, 3.5. Модель точки пространства Е4 |
|
||||||||||
сти XxYxT (рис. 3.6). |
|
|
|
|
|
|
|||||||
Точка |
С(х, |
0, |
z, |
0) |
принадлежит |
плоскости |
|
XxZ, а |
точка |
||||
D(0, 0, 0, г) |
принадлежит оси |
Т. Однако на практике не пользуются |
|||||||||||
чертежом, содержащим все шесть проекций, т.к. половина из них
лишние. |
Кроме того, |
для п—мерного |
пространства |
получаются |
|||||
n\ |
_п{п-\) |
|
|
|
ZJ |
|
|
||
|
|
|
|
|
|||||
2 и > _ 2 ) ! ~ |
2 |
|
|
|
|
|
|||
Bi |
|
|
|
As |
|||||
проекций. |
Поэтому |
|
|
0=0,4 |
|||||
|
|
|
|
|
|
||||
используют |
чертеж |
|
|
|
|
\ |
|
||
|
|
|
|
|
|
|
|||
с п-\ проекциями. |
|
|
|
|
|
|
|
||
Из |
совпадения |
6 |
|
|
|
|
|
|
|
простейшей |
графи |
|
|
Сь=Сй |
el |
|
l 4 |
||
В, |
|
|
|
||||||
|
|
|
|
|
|
|
|||
ческой модели про X- |
|
|
|
|
|
|
|
||
77=Z7 |
|
|
0=0^-- |
|
|
Y.T |
|||
странства Е3, полу |
|
|
|
|
|
|
|
||
ченной |
аксиомати |
Вт |
1 |
|
|
|
|
|
|
ческим путем, с мо |
|
|
|
|
|
||||
|
|
|
Y |
|
|
||||
делью Монжа этого |
|
|
|
|
|
||||
пространства, полу- |
Рис. 3.6. Модель точек пространства Е4 |
||||||||
|
|
|
|
|
|
|
|||
ченной конструктивным путем, следует, что некоторые аксиоматиче ские модели абстрактного пространства могут быть реализованы на основе конструктивной взаимосвязи между пространством прообра зов и его моделью.
Из рассмотрения взаимного по ложения пары точек относительно плоскостей проекций следует, что па ра точек может принадлежать одной проецирующей прямой, или одной проецирующей плоскости и тогда на одной из плоскостей проекций при сутствуют совпавшие одноименные проекции этих точек. Такие точки на зываются конкурирующими. Напри мер, точки А и В принадлежат про ецирующей Z -плоскости, перпенди кулярной плоскости /7,, а точки С , D
принадлежат проецирующей прямой, перпендикулярной гиперпло скости X х Z х Т (рис. 3.7).
Кроме основных проекций, полученных проецированием на ос новные плоскости проекций //,, //2, /73, точка может иметь допол нительные проекции, полученные ортогональным проецированием на плоскости, отличающиеся от основных. Дополнительная плоскость проекций образует с одной из основных плоскостей проекций либо с
другой дополнительной плоскостью проекций |
пару взаимно перпен- |
|||||||
|
|
дикулярных |
плоскостей. |
Па рисун |
||||
|
|
ке 3.8 представлен чертеж, содержа |
||||||
|
|
щий |
построения |
дополнительных |
||||
х rii |
|
проекций АА |
и |
А} |
точки |
А е Е3, за |
||
|
данной основными проекциями Л,, А2 |
|||||||
А А. |
А, |
|||||||
. Эти |
построения |
соответствует из |
||||||
|
||||||||
|
Ахг |
вестному в начертательной |
геометрии |
|||||
|
методу замены |
плоскостей |
проекций, |
|||||
|
|
|||||||
|
П1 |
при котором |
основной объект про |
|||||
|
странства - точка, неизменна в своем |
|||||||
|
|
|||||||
Рис. 3.8. Дополнительные |
положении, а в парах плоскостей про |
|||||||
|
|
|
|
|
|
|||
проекции точки |
|
екций |
происходит |
последовательная |
||||
пространства £, |
|
замена одной из плоскостей проекций |
||||||
60 |
61 |

на новую, дополнительную: |
|
X, I1! |
х А |
Я , |
2П5 |
Из метрических свойств последовательной замены плоскостей ортогональных проекций вытекает алгоритм построения дополни тельных проекций точки А:
(А2,А1) -> АА(А7АХ = АХХАА),(АХ,АА) -> A5(ASAXX = АХ2А}),...
|
3.2. |
Моделирование прямой линии |
||
Прямая |
в евклидовом пространстве |
|
||
определена парой несовпадающих точек. |
|
|||
Построив модели этих точек и соединив |
|
|||
прямыми линиями пары их одноименных |
|
|||
проекций, получим прямые - проекции |
/7, /77 |
|||
прямой линии пространства (рис. 3.9). С |
/7/ |
|||
|
|
|
||
другой стороны, прямая линия простран |
|
|||
ства Е„, на |
основании |
формулы (1.1), |
|
|
принадлежит 2(и - 1)-параметрическому |
Рис. 3.9. Модель прямой |
|||
множеству прямых этого пространства, |
||||
линии пространства Е4 |
||||
поскольку: |
D™ = (1 +1) -(n-l) = 2(п - 1 ) . |
|||
|
||||
Произвольные пары прямых на плоскости |
образуют также 2 ( я - 1 ) - |
|||
параметрическое множество, поскольку |
на плоскости |
множество |
прямых, в соответствии с формулой |
(1.1), двухпараметрично: |
|
D™ = (1 +1) • (2 -1) = 2. Следовательно, на чертеже, как |
и на его ак |
|
сиоматическом аналоге, прямая линия моделируется in -1) прямыми ((п -1) ортогональными проекциями прямой).
В зависимости от расположения прямой линии пространства от носительно плоскостей проекций различают прямые общего и частно го положений.
3.2А. Прямая общего положения
Если в системе ортогональных плоскостей проекций прямая ли ния не параллельна ни одной гиперплоскости, натянутой на оси про екций, то она называется прямой общего положения относительно этой системы плоскостей проекций. Па рисунке 3.9 приведена модель
такой прямой в системе X п2,п: з . Исходя из конструктивного пред
Я ,
ставления моделей точки и прямой линии пространства на рассмат риваемой его графической модели, можно сформулировать критерий принадлежности точки прямой линии: точка принадлежит прямой ли нии в пространстве, если модель точки принадлежит модели прямой, или в терминах чертежа Монжа - если проекции точки принадлежат одноименным проекциям прямой. Так точка А/принадлежит прямой
АВ, поскольку м{ е АХВ,, М2 е А2В2, Мъ е А3В3.
3.2.2.Прямые уровня
Если прямая параллельна одной из гиперплоскостей проекций, то она называется прямой уровня относительно этой гиперплоскости. На рисунке 3.10 для пространства ЕГ изображены:
1. Горизонтальная пря мая уровня h (горизонтать h II Я,), при ЭТОМ lij IIX .
х- |
|
2. |
Фронтальная |
прямая |
||||
|
уровня |
/ |
(фронталь |
/ , 7 Я Д |
||||
|
|
|||||||
|
|
при этом |
/, ИХ. |
|
|
|||
|
|
Линии уровня обладают |
||||||
|
|
метрическими |
свойствами. |
|||||
Рис. 3.10. Модели прямых уровня |
Проекция |
л, 5, |
отрезка АВ |
|||||
горизонтали |
h |
представляет |
||||||
пространства |
Е} |
|||||||
собой |
длину |
отрезка |
АВ. На |
|||||
|
|
|||||||
основании известного в школьном курсе стереометрии определения
угла между прямой и плоскостью следует, |
что угол а |
А, л X |
есть |
|
угол а = А л /7, между горизонталью h |
и плоскостью проекций |
fl2. |
||
Проекция C2D2 отрезка CD фронтали |
/ |
представляет собой длину |
||
отрезка CD, а угол р = /2лХ есть угол |
р |
= / л Я, |
между фронта- |
|
лью и плоскостью проекций я, • |
|
|
|
|
3.2.3.Проецирующие прямые
Рхли прямая перпендикулярна гиперплоскости проекций, то она называется проецирующей относительно этой плоскости.
63
62
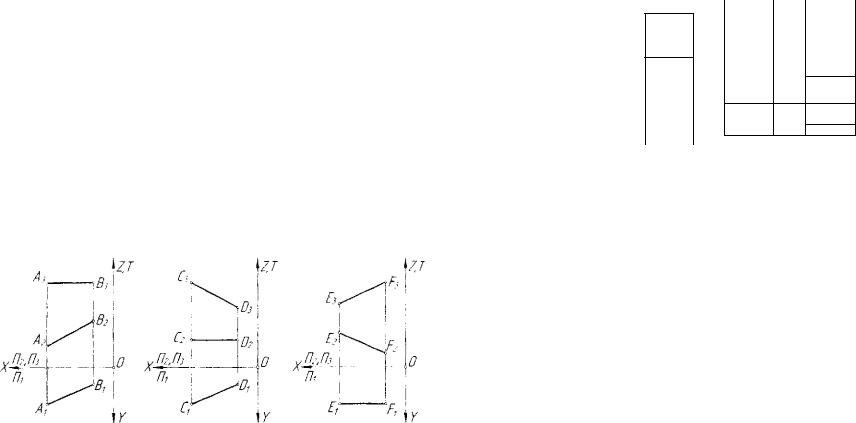
На рисунке 3.11 для пространства |
|
изображены: |
аг |
1.Горизонтально-проецирующая ^
прямая |
о 1 Я р при этом а2 ± X , а, - |
Х~^" |
.г, |
точка. |
|
/7/ |
|
|
|
|
|
2. |
Фронтально-проецирующая |
|
|
прямая |
ЫП2, при этом Ьх 1 X , Ъ2 - |
Рис. 3.11. Модели |
|
точка. |
|
||
|
|
|
|
3. |
Профильно-проецирующая |
проецирующих прямых |
|
прямая |
с!П:„ при этом, с, // X , с, // X , |
пространства |
£3 |
г, - точка.
3.2.4.Прямые уровня пространства Е4
На рисунке 3.12 изображены прямые, параллельные гиперпло скостям XxYxZ,XxYхТ и XxZxT.
Рис. 3.12. Модели прямых уровня относительно гиперплоскостей проекций пространства Е.
На рисунке 3.13 изображены прямые, параллельные плоскостям
XxY, XxZ, ХхТ.
Сз. |
Оз |
Z T |
|
|
|
|
|
Ез
А? в2
Е?
х- П?,Пз с?
I
с,
Рис. 3.13. Модели прямых уровня относительно плоскостей проекций пространства Е4
3.2.5.Проецирующие прямые пространства Е4
На рисунке 3.14 изображены прямые, перпендикулярные гиперп
лоскостям |
А ' х К х / , X xYxT, X xZxT |
и |
плоскостям X х Y |
XхZ, |
XхТ. |
|
|
|
zj |
|
d3 |
02 |
С2 |
|
|
уПгЛз |
0 |
а* |
с, |
Рис. 3.14. Модели проецирующих прямых пространства Е4
64
65
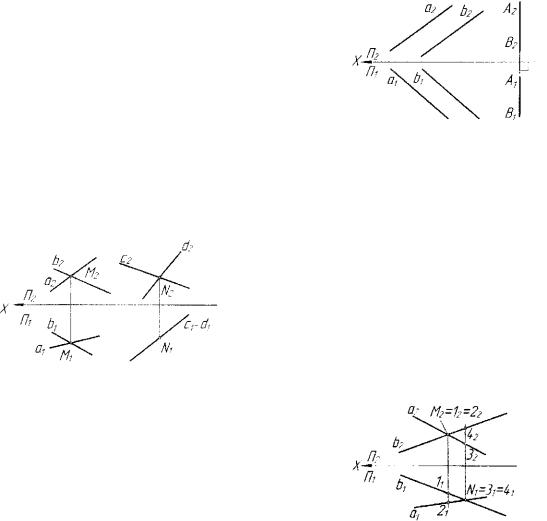
3.3. Моделирование взаимного расположения прямых линий в пространстве
В общем случае две прямые в пространстве Еп не пересекаются, так как в соответствии с формулой размерности пространства пересе чения s = m + q-n, выведенной в разделе 1.7.2, получаем j = 1 +1 - и < 0, и > 3. Но две прямые в плоскости могут пересекаться как в собственной, так и в несобственной точке, поскольку s = l + l - 2 = 0. Таким образом, в пространстве две прямые линии мо гут быть пересекающимися, параллельными и скрещивающимися. Рассмотрим модели этих прямых.
3.3.1.Пересекающиеся прямые
На рисунке 3.15 представлены изображения на графической мо дели пространства £, пересекающихся прямых. Прямые а и Ъ пере
секаются |
в |
точке. |
Действи |
|
||||
тельно, |
ПОСКОЛЬКУ |
М 2 £ а2 И |
|
|||||
Л/, е в,, то следует, что М е а . |
|
|||||||
Но |
М, |
е |
Ъг |
и |
м, с 6,, |
следо |
|
|
вательно, |
М е h . Таким |
обра |
|
|||||
зом, две различные прямые а и |
|
|||||||
Ъ имеют общую точку, то есть |
|
|||||||
они |
пересекаются. |
Очевидно, |
|
|||||
точка N также является общей |
|
|||||||
точкой |
двух |
различных |
пря |
Рис. 3.15. Модели |
||||
мых |
с |
и |
d, |
то |
есть |
N = cf]d . |
пересекающихся прямых |
|
Прямые |
с |
и |
d |
называются го |
пространства Е3 |
|||
ризонтальноконкурирующими, потому, что любая пара их точек на горизонтально-проецирующей прямой является горизонтальноконкурирующими.
3.3.2.Параллельные прямые
Две прямые линии в пространстве Е3 могут быть параллельными, так как в соответствии с формулой (1.5) степень их параллельности
0+1 |
= 1. Изображение параллельных прямых представлено |
равна рII- 1 |
|
|
66 |
на рисунке 3.16. Так как а211Ъ2 и а,//Ъх, то прямые а и Ъ в простран стве параллельны, при этом моделью несобственной точки пересече-
[2 |
ния |
параллельных |
прямых |
|||
|
af]b = Л/м |
является пара иесоб- |
||||
q |
ственных точек |
а2Г\Ь2 = М 2о. и |
||||
|
а,П*1=Л/1оо, принадлежащих |
|||||
|
несобственной |
прямой |
плоско- |
|||
1 |
сти рассматриваемой графиче- |
|||||
£ |
ской |
модели |
пространства. |
|||
1 |
Критерий |
параллельности |
двух |
|||
Рис. 3.16. Модели параллельных |
прямых в |
пространстве |
в |
тер- |
||
прямых пространства Е3 |
м и н а х |
ч Ф т е ж а Монжа |
может |
|||
|
быть |
сформулирован |
следую |
|||
щим образом: если одноименные проекции прямых общего положе ния параллельны, то и сами прямые в пространстве параллельны. Не трудно проверить, что прямые АВ и CD не параллельны, несмотря на то, что А2В2IIC2D2 и АХВХIICXDX. Для проверки паратлельности необ ходима дополнительная проекция этой пары прямых.
3.3.3.Скрещивающиеся прямые
Прямые, образующие в пространстве между собой ненулевое кратчайшее расстояние и угол, не равный 0" и 180°, называются скре щивающимися. Следовательно, это прямые, которые не являются пе ресекающимися и параллельными. Изображение скрещивающихся прямых на модели пространства представлено на рисунке 3.17. Пока
жем, что а2 и Ьх,Ьг ~ это модели (проекции) двух прямых а и Ъ, скре щивающихся в пространстве. Предпо ложим, что м2 - a2f]b2 есть фронталь ная проекция точки М - af]b . Тогда на основании свойства проекций пересе кающихся прямых горизонтальной про екцией должна быть точка М, = а, Г) Ъх • Но а,П&] - Nх Ф Мх • Следовательно, М, Ф axf]bx и поэтому М Ф af]b . Ана логично доказывается, что Л' Ф а Г) Ъ .
67
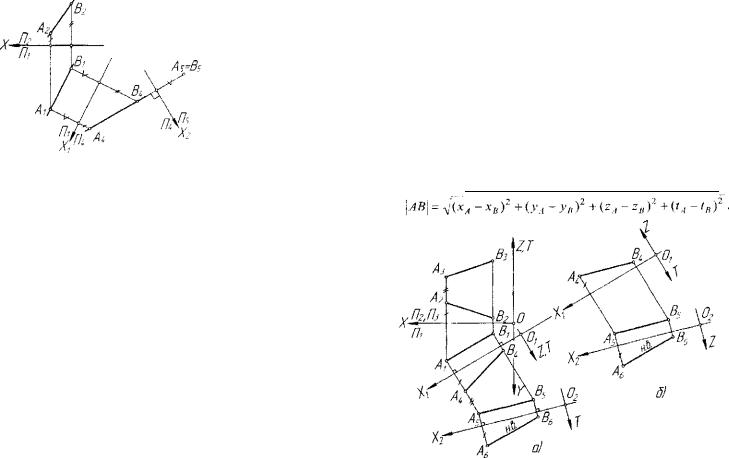
Таким образом, прямые, заданные на графической модели, не являют ся пересекающимися и не являются параллельными, то есть они скрещиваются. Проекции скрещивающиеся прямых характеризуются наличием проекций двух пар конкурирующих точек 1(1,, 12), 2(2,, 2 2) И 3(3,, 3 2 ), 4(4,, 4 , ) .
3.3.4.Дополнительные проекции прямой
|
Как в случае точки, для прямой линии можно построить допол |
|||||||
нительные проекции. Пусть на |
|
|||||||
графической |
модели |
задана |
|
|||||
прямая |
АВ |
общего положения |
|
|||||
(рис. 3.18). Используя алгорит |
|
|||||||
мы |
построений |
дополнитель |
|
|||||
ных |
проекций точки |
(п. 3.1), |
|
|||||
построим |
несколько |
дополни |
|
|||||
тельных |
проекций |
прямой ли |
|
|||||
нии |
АВ. В |
системе плоскостей |
|
|||||
проекции |
Л , — - , |
где |
доиолни- |
Рис. 3.18. Модель дополнительных |
||||
|
|
|
|
|
|
|
||
тельная |
плоскость |
я,, удовле |
проекций прямой линии |
|||||
пространства Е, |
||||||||
творяет |
условиям: |
Я 4 ± Л | , |
||||||
|
||||||||
Я4 // АВ |
, прямая |
АВ |
имеет проекции A,Bt, А4В4, причем, на основа |
|||||
нии метрических свойств прямой линии уровня (п. 3.2.2), /шина от
резка |
ААВ4 |
есть длина отрезка АВ прямой линии. В системе плоско- |
||||
стой |
проекции |
Л2 |
, где |
плоскость я5 удовлетворяет |
условиям: |
|
|
|
|
|
П. |
|
|
Я5 1 |
п4, |
11, |
АВ , прямая |
АВ имеет проекции: А4В4 и |
А5 = В5, то |
|
есть является проецирующей. Из логики геометрических построений на рисунке 3.13 можно сделать следующие выводы:
1. Построениям первой дополнительной проекции А4В4 соответ ствуют преобразования прямой линии из общего положения в поло жение линии уровня, причем преобразованиям подвергается система
основных плоскостей проекций Х~2 , преобразующаяся в систему
68
Xt положение же прямой линии АВ в пространстве остается не
изменным. Выполненные построения соответствуют решению метри
ческой задачи на определение длины отрезка прямой линии.
2. Построениям второй дополнительной проекции (-)А5 - (•)#, соответствуют преобразования прямой линии из общего положения в
проецирующее, при этом |
имеют место |
преобразования систем |
плос- |
|||||
|
„ |
Я , |
v |
Я, |
„ |
Я 4 |
|
|
костей |
проекции |
л —- —> лх |
|
|
> л2 |
— при неизменном в |
про- |
|
|
|
|||||||
|
|
Я] |
|
|
Я 4 |
|
Я5 |
|
странстве положении прямой |
АВ. |
|
|
|
||||
3. |
Преобразование прямой линии из общего положения в |
про |
||||||
ецирующее возможно только посредством выполнения промежуточ ного этапа преобразования этой прямой в положение линии уровня.
3.3.5.Дополнительные проекции прямой линии пространства Е„
Пусть на графической модели пространства ЕА задана прямая общего положения (рис. 3.19) АВ{АхВи А2В2. Л3В3) •
Вычислить длину отрезка АВ в пространстве £4 аналитически не представляет труда:
Рис. 3.19. Модель дополнительных проекций прямой пространства Et
69
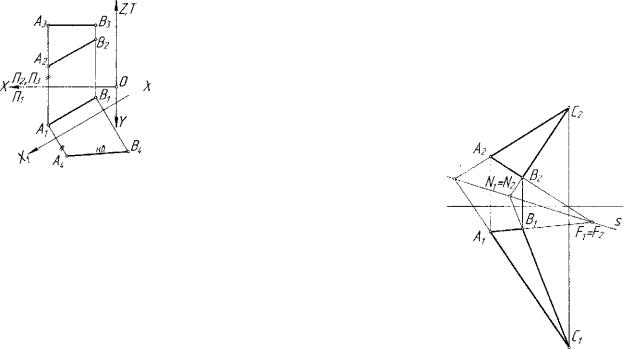
На чертеже вводятся новые гиперплоскости проекций, парал лельные отрезку АВ. На рисунке 3.19 такой гиперплоскостью являет ся OxXxZT , при этом 01Х1II АХВХ. Отрезки А4В4 и А5В5 являются мо делью отрезка АВ в пространстве Е3 с системой координат OxXxZT . Далее поступаем аналогично предыдущему пункту, т.е. выбираем плоскости проекций параллельно какой-либо проекции отрезка - проекции А4В4 или А5В5. На рисунке 3.19, а) выбрана плоскость 02Х2Т, параллельная отрезку АВ: ОгХ2 IIА5В5.
Для большей наглядности на рисунке 3.19, б) показаны эти же процедуры, но предварительно выполнен поворот плоскости проек ций oxXxZ на 180° вокруг оси ОхХх. После этого аналогия с черте жом пространства Е3 очевидна.
Приведем еще несколько частных случаев расположения отрезка АВ относительно плоскостей и гиперплоскостей проекций. На рисун
ке |
3.20, |
а) |
отрезок |
|
|
|
|
|
и |
|
АВ |
параллелен |
ги |
|
|
|
|
|
|||
|
|
|
|
Вз |
||||||
|
Аз |
|
|
|||||||
перплоскости проек |
|
|
|
|
|
|
||||
ций |
OXYZ |
. Поэтому |
|
А2 |
|
|
|
\в2 |
||
для |
определения |
его |
|
|
|
|
||||
|
П2,Пз |
|
|
|
о |
|||||
натуральной |
величи |
|
|
|
|
|||||
|
lli |
|
|
|
||||||
ны достаточно одно |
|
|
|
|
в; |
|||||
го |
преобразования |
|
А; |
|
|
|
|
|||
|
|
|
|
|
||||||
плоскости проекций. |
|
|
|
|
|
|||||
|
На рисунке |
3.20, |
|
|
|
|
|
|
||
б) |
отрезок |
АВ |
па |
а) |
61 |
|
|
|||
раллелен |
плоскости |
|
|
|||||||
|
|
|
|
|
|
|||||
проекций |
OXY . По |
Рис. 3.20. Частные случаи параллельности прямой |
||||||||
|
|
|
|
|
|
|||||
этому \лхвх I = \ АВ\ . |
пространства Е4 |
|
|
|
||||||
|
|
|
|
|
|
|||||
|
Обобщение |
на |
w-мерное пространство не составляет труда: |
|||||||
1 1 |
1 " |
|
|
2 |
|
|
|
|
|
|
|
A2Z(xA,i |
~ x B , i ) • |
Нахождение длины отрезка АВ |
графически |
||||||
можно предложить в виде упражнения.
3.4.Моделирование плоскости
На рассматриваемой графической модели точка М пространства Е3 моделируется парой точек м, я М2 на прямой пучка с несобст-
венным центром. Следовательно, всему множеству точек пространст ва соответствует в плоскости модели два совмещенных поля точек - поле точек "Мх" и поле точек "М2"• Установление некоторого соот ветствия между полями точек "Л/," и " М 2 " приводит к моделирова нию этим соответствием определенных множеств точек пространства Е3: плоскостей, поверхностей.
В соответствии с аксиомой стереометрии, через любые три точки, не принадлежащие одной прямой, проходит единственная плоскость. Следовательно, задание моделей указанных трех точек означает зада ние модели плоскости пространства. Нетрудно подсчитать парамет рическое число этой модели. В соответствии с формулой (1.1) для плоскости трехмерного евклидова пространства получаем:
D™ = ( 3 - 2 ) - ( 2 + 1) = 3.
Пусть на графической модели заданы три пары соответственных точек А1,А2; ВХ,В2; С , , С 2 (рис. 3.21). Эти пары определяют модель конкретной плоскости пространства. Пар соответственных точек на каждой прямой пучка с несобственным центром - однопараметриче ское множество. На трех фиксированных прямых пучка АхА->, ВХВ2, С , С 2 получаем трехпараметрическос множество пар соответственных точек. Таким образом, параметрическое число модели плоскости про-
|
странства |
также |
равно |
трем. |
|||||
|
Три |
пары |
соответственных |
||||||
|
прямых |
АХВХ, А2В2; А1С1, |
А2С2; |
||||||
М,=М2 |
ВХСХ, В2С2 пересекаются в трех |
||||||||
точках одной прямой 5, кото |
|||||||||
|
|||||||||
п, |
рая |
является |
двойной, |
то |
есть |
||||
/7/ |
состоит |
из |
самосоответствен |
||||||
ных точек, таких как, напри |
|||||||||
|
|||||||||
|
мер, |
|
МХ=М2, |
NX = N2, |
|||||
|
Fx - F2 • Соответствие, которым |
||||||||
|
моделируется |
на |
рассматри |
||||||
|
ваемой |
графической |
модели |
||||||
|
плоскость |
пространства, назы |
|||||||
|
вается |
родством или |
перспек |
||||||
|
тивно-аффинным |
соответстви |
|||||||
Рис. 3.21. Родство-модель плоскости |
ем [6, 16, 24]. Прямая s двой |
||||||||
ных |
точек |
называется |
осью |
||||||
пространства Е3 |
|||||||||
|
|
|
|
|
|
|
|
||
70
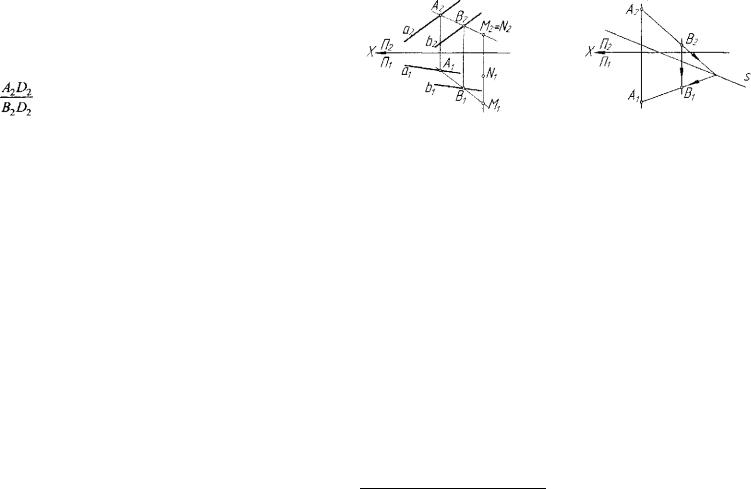
родства, а направление параллельных прямых АХА2, ВХВ2, СХС2 - на правлением родства. Исходя из параметрического числа модели плос кости-родства, следует, что оно может быть задано осью s родства и нарой соответственных точек, например, АХ,А2. Родство сохраняет принадлежность, например, Г), е dx <-> D2 «= d2 и простое отношение
|
AXDX |
трех точек, например, |
. В методе Монжа прямая s пред- |
ставляет собой линию пересечения моделируемой плоскости про странства и биссекторной плоскости четных четвертей, образуемых плоскостями проекций #, и я 2 . Исходя из параметрического числа родства, равного трем, оно может быть задано (кроме рассмотренных выше заданий тремя парами соответственных точек, а также осью родства и парой соответственных точек): двумя парами соответствен ных прямых; парой соответственных точек и парой соответственных прямых. Способам задания родства на графической модели простран ства соответствуют известные способы задания плоскости в про странстве (кроме отмеченного способа задания тремя точками): точ кой и прямой, двумя пересекающимися прямыми, двумя параллель ными прямыми. Для удобства решения различных позиционных, аф финных и метрических задач на графической модели часто применя ется задание плоскости треугольником, вытекающим из основного способа задания плоскости тройкой точек, не принадлежащих одной прямой.
3.4.1. Плоскость общего положения
В методе Монжа существует понятие плоскости общего и част ного положений. Если плоскость не перпендикулярна ни одной из плоскостей проекций я , и и2,то она называется плоскостью общего положения относительно этой системы плоскостей проекций. Крите рий задания плоскости на чертеже Монжа может быть сформулиро ван следующим образом: плоскость считается заданной на чертеже, если модель плоскости на нем позволяет определить принадлежность любой точки пространства этой плоскости. Для конструктивного оп ределения принадлежности точки к плоскости применяется следую щее условие: точка принадлежит плоскости, если она принадлежит линии этой плоскости. Из построений на рисунке 3.22 следует, что точка М принадлежит плоскости (alib), заданной параллельными
72
Рис. 3.22.1 1ринадлсжность |
Рис. 3.23. Принадлежность |
точки к плоскости |
точки к плоскости простран- |
нроетранства Къ |
ства £3 > заданной родством |
прямыми а и Ь, поскольку принадлежит линии АВ этой плоскости, а точка N не принадлежит плоскости. На рисунке 3.23 приведено по строение модели точки В пространства, принадлежащей плоскости, заданной осью родства <?. и парой соответственных точек Л,, А7. Мо дель точки В построена по условию задания точки В2 - одной из двух точек, моделирующих точку В (искомой является точка в,).
3.4.2.Плоскости уровня
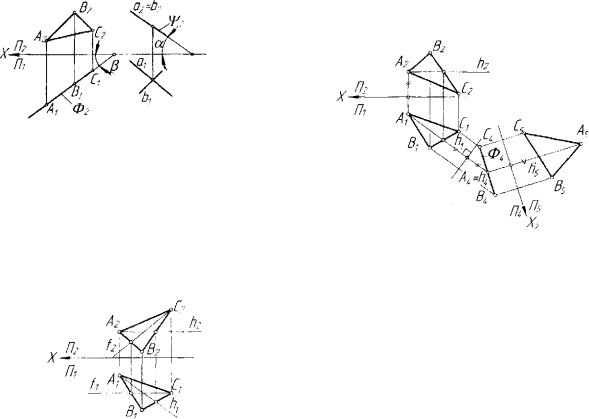
Если плоскость пространства параллельна плоскости проекций, то она называется плоскостью уровня относительно этой плоскости проекций. На рисунке 3.24 изображены горизонтальная L//77, и фронтальная д// II2 плоскости уровня, при этом t2llX и Ах!/Х, Z2 и д, - соответственно фронтальный след плоскости £ и горизонталь ный след плоскости Д.
|
х2 |
|
|
|
|
|
|
|
Любая плоская фшура в плос |
|||||
|
|
|
|
|
|
|
|
кости уровня отображается на соот |
||||||
|
|
|
|
с2 |
и2 |
-у |
|
|
ветствующую |
плоскость |
проекций |
|||
Х |
- |
|
|
|
|
|
|
|
без искажений. Например, |
д л ^ с , |
||||
|
/7/ А, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
\ |
/ |
|
|
А1=а1=Ь1 |
представляет |
собой |
истинное изо |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
бражение |
ДЛВС ; угол |
а = а2 л Ъ2 |
||||||
|
|
V |
|
|
|
|
||||||||
|
Рис. 3.24. Плоскости уровня |
есть угол |
а = а лЬ |
двух |
пересе |
|||||||||
|
кающихся |
прямых |
а и |
Ь |
в про |
|||||||||
|
|
пространства |
£, |
|
||||||||||
|
|
|
странстве. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
73 |
|
|
|
|
|
3.4.3.Проецирующие плоскости
Если плоскость пространства перпендикулярна плоскости проек ций, то она называется проецирующей относительно этой плоскости
проекций. На рисунке 3.25 изо |
|
|||
бражены горизонтально - и фрон |
|
|||
тально-проецирующие |
плоскости |
|
||
соответственно |
Ф ± /7, |
и ч/ 1 П2, |
|
|
при этом Ф, и |
- наклонные в |
|
||
общем случае прямые - следы |
|
|||
плоскостей. Угол в = ФхЛХ = ФЛП2 |
|
|||
есть угол между плоскостями |
Ф и |
|
||
//,, а угол а = Ч , л X = Ч/ |
л /7, |
Рис. 3.25. Проецирующие плоскости |
||
|
|
|
|
|
есть угол между плоскостями ЧУ и |
пространства £3 |
|||
ПI •
3.4.4.Прямые уровня в плоскости
В любой плоскости Ф пространства существует двухиараметрическое множество прямых линий. На основании формулы (1.5) прямая и плоскость в этом пространстве вполне параллельны, по скольку степень параллельности для них
равна: рц = —-— = 1. Укажем в простран стве еще одну плоскость ЧУ такую, что Ф
иY не параллельны. Тогда в плоскости
Фможно выделить единственный пучок прямых с несобственным центром, па раллельных линий пересечения Ф п Ч ' и, следовательно, параллельных плоскости
ЧУ. Если в качестве плоскости ЧУ рас сматривается некоторая плоскость про екций, причем Ф и ЧУ не параллельны, то прямые указанного пучка представляют
собой прямые уровня относительно этой плоскости проекций. По скольку линия уровня обладает метрическими свойствами (п. 3.2.2), то принадлежность линии уровня некоторой плоскости пространства может быть использована для решения множества метрических задач,
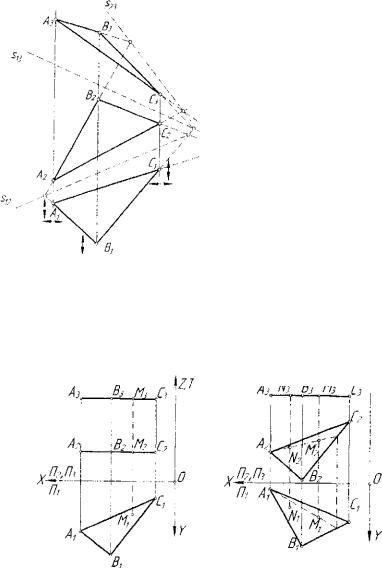
относящихся к этой плоскости. На рисунке 3.26 приведены построе ния двух линий уровня / ( / , , / 2 ) / / Я 2 и h(hx,h2)H Я , , принадлежащих плоскости Ф(АЛВС).
3.4.5.Дополнительные проекции плоскости
|
|
|
|
|
|
Пусть |
на |
графиче |
|||
|
|
|
|
|
ской |
модели |
простран |
||||
|
|
|
|
|
ства |
задана |
плоскость |
||||
|
|
|
|
|
Ф(ААВС) |
общего поло |
|||||
|
|
|
|
|
жения (рис. 3.27). По |
||||||
|
|
|
|
|
строим в этой плоскости |
||||||
|
|
|
|
|
Л И Н И Ю |
У Р О В Н Я |
//(/;,. А2). |
||||
|
|
|
|
|
Поскольку |
прямая |
и |
||||
|
|
|
|
|
плоскость |
в пространст |
|||||
|
|
/77/ |
|
|
ве |
£, |
вполне |
перпенди |
|||
|
|
|
|
|
кулярны |
(п. |
1.7.3), |
то |
|||
|
|
|
|
|
можно |
провести |
допол |
||||
|
Рис. 3.27. Дополнительные проекции |
|
нительную |
|
плоскость |
||||||
|
|
проекций |
П4±п, |
что |
|||||||
|
плоскости пространства Е3 |
|
|||||||||
|
|
соответствует |
построе |
||||||||
|
|
|
|
|
|||||||
ниям |
на чертеже оси |
проекций Хх |
±.hx. |
В |
образующейся |
системе |
|||||
плоскостей |
проекций |
Хх^- прямая |
h(hx,(-)h4) |
является проецирую- |
|||||||
|
|
|
П4 |
|
|
|
|
|
|
|
|
щей относительно дополнительной плоскости проекций |
|
п4. |
По |
||||||||
скольку плоскости Ф принадлежит линия |
h, перпендикулярная плос |
||||||||||
кости |
п 4, |
то получаем перпендикулярность |
плоскостей |
|
Ф I |
п4 |
|||||
(п. 1.7.3) и, следовательно, плоскость Ф |
является проецирующей в |
||||||||||
^П\
системе плоскостей проекций Хх—. Введение второй дополнитель-
П4
ной плоскости проекций п4 по условиям Л„ // Ф, /7 4 _1_ Я , , приводит к образованию системы плоскостей проекций, в которой исходная плоскость Ф является плоскостью уровня относительно я 4. Из логи ки выполнения построений, приведенных на рисунке 3.27, следуют выводы:
74 |
75 |
|
1. Построениям первой дополнительной проекции Ф 4 заданной плоскости Ф(ААВС) соответствуют преобразования плоскости из общего положения в проецирующее. Преобразованиям подвергается
система основных плоскостей проекций ^ ^ ~ > преобразующаяся в
систему Л] - • - , положение же плоскости Ф остается неизменным.
ПА
2. Построениям второй дополнительной проекции (дл5Я5С3) соответствуют преобразования плоскости Ф из общего положения в положение плоскости уровня. При этом имеют место преобразования
" |
Г Я 2 ^ у |
U\ _^ у ПА |
||||
систем плоскостей проекции л |
|
>лх |
—>л2 |
|
|
при неизмен- |
|
|
|
||||
|
Пх |
ПА |
П5 |
|||
ном положении исходной плоскости Ф. Этим преобразованиям соот ветствует решение задачи определения действительного изображения плоской фигуры, расположенной в плоскости общего положения. Ре зультатом решения этой задачи в рассматриваемом случае является
AA,BSCS = А ABC .
3. Преобразования плоскости из общего положения в положение плоскости уровня возможно только при условии выполнения проме жуточного этапа - преобразования этой плоскости в проецирующее положение.
3.5.Моделирование плоскости пространства Еп
Всоответствии с аксиомами принадлежности плоскость задается тремя точками вне зависимости от размерности пространства. Для ее задания требуется 3 ( « - 2 ) параметров. На рисунке 3.28 приведена модель плоскости ABC пространства £ 4 . Общее число параметров, подсчитанное по модели, равно 12, но одна из проекций, например, AxBxCt, допускает изменение положений точек Ах, Вх, Сх в двух на правлениях. 11ри этом сама плоскость ABC не меняет своего положе ния в пространстве £ 4 . Поэтому остается 12 - 6 = 6 независимых па раметров. Проекции АХВХСХ и А2В2С2 связаны родством с осью sX2, и проекции А2В2С2 и АЪВ3С2 - родством с осью .?23. Направление род ства - одно для обоих соответствий. Прямые si2 и s,3 есть прямые пе ресечения данной плоскости ABC с биссекторной гиперплоскостью,
76
|
образованной |
биссектор- |
||||||
|
ными |
плоскостями |
первых |
|||||
|
четвертей |
|
пространств |
|||||
|
E3(X,YtZ) |
и |
|
E3(X,z,T). |
||||
|
Легко |
можно |
построить |
|||||
|
ось |
.г,, |
родства, |
связы |
||||
|
вающего |
проекции |
Л, Я, С, |
|||||
|
и А3В3С3. Плоскость ARC |
|||||||
|
есть |
плоскость |
общего |
гю- |
||||
. - |
ложения. |
Плоскостей |
ча |
|||||
|
стного |
положения |
может |
|||||
|
быть несколько различных |
|||||||
|
видов: |
|
|
|
|
|
||
|
- |
плоскости, |
перпендику |
|||||
|
лярные |
|
гиперплоскости |
|||||
|
проекций; |
|
|
|
||||
Рис. 3.28. Моделирование плоскости |
~ |
плоскости, |
перпендику- |
|||||
прострапства Е, родством |
ЛЯ |
РНЫе |
" J l ~ ™ |
проек |
||||
|
ции; |
|
|
|
|
|
|
|
-плоскости, параллельные гиперплоскости проекций;
-плоскости, параллельные плоскости проекций. Рассмотрим их модели для пространства Е4.
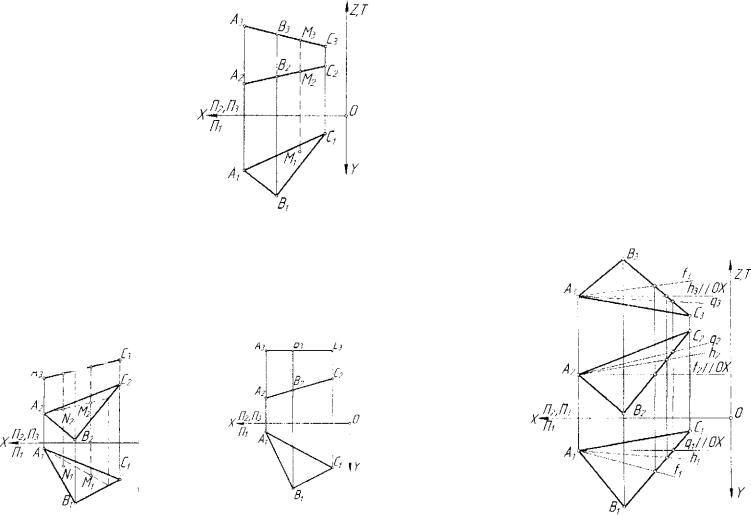
На рисунке 3.29 изображена плоскость ABC, параллельная плос-
\ZT
Рис. 3.29. Плоскость пространства Е4, |
Рис. 3.30. Плоскость пространства, |
параллельная плоскости OXY |
параллельная гиперплоскости OXYZ |
77 |
|
кости проекций OXY . Ее уравнение есть z-const, t = const, если считать, что проекции точек с индексом 3 имеют координаты (х, t), а проекции с индексом 2 - координаты (x,z) (см. рис. 3.1).
Очевидно, |
|
что |
проек |
|
|
|
||||
ция AlBlCl |
треугольника |
|
|
|
||||||
ABC, как и любой другой |
|
|
|
|||||||
фигуры, лежащей в плоско |
|
|
|
|||||||
сти |
ABC, не |
искажена. |
То |
|
|
|
||||
есть АХВХСХ |
- |
есть |
нату |
|
|
|
||||
ральная |
величина треуголь |
|
|
|
||||||
ника ABC. М е ABC . |
|
|
|
|
|
|||||
На |
рисунке |
3.30 |
|
изо |
|
|
|
|||
бражена |
плоскость |
|
ABC, |
|
|
|
||||
параллельная |
гиперплоско |
|
|
|
||||||
сти |
проекций |
|
OXYZ |
. |
Ни |
|
|
|
||
А2В2С2, ни А]В]С1 не |
явля |
|
|
|
||||||
ются |
натуральными |
изо |
|
Рис. 3.31. Плоскость пространства £ 4 , |
||||||
бражениями |
треугольника |
перпендикулярная гиперплоскости OXZT |
||||||||
ABC. М е ABC , N £ ABC . |
||||||||||
|
|
|
||||||||
На рисунке |
3.31 |
изображена плоскость |
ABC, перпендикулярная |
|||||||
гиперплоскости |
проекций OXZT |
. Другими словами, плоскость ABC |
||||||||
параллельна оси |
OY. |
Поэтому ее пересечение с гиперплоскостью |
||||||||
OXZT |
есть прямая, проекции которой А3В3С3 |
и А2В2С2. М е ABC . |
||||||||
|
|
|
|
|
|
ZT |
|
|
\ZJ |
|
|
|
|
|
|
|
|
|
|
||
о
Рис. 3.32. Плоскость пространства £4 |
Рис. 3.33. Плоскость, принадлежащая |
перпендикулярна плоскости ОХТ |
гиперплоскости частных положений |
|
в пространстве £ 4 . |
|
78 |
На рисунке 3.32 изображена плоскость ABC, перпендикулярная плоскости ОХТ . Точнее сказать, что ЛВС принадлежит гиперплоско сти, перпендикулярной плоскости ОХТ . М е ABC , N г ABC .
На рисунке 3.33 плоскость ABC расположена в гиперплоскости, параллельной гиперплоскости OXYZ , перпендикулярно плоскости проекций OXZ .
3.5.1. Прямые уровня в плоскости пространства £4
В плоскости общего положения пространства Е4 можно выбрать прямые уровня относительно гиперплоскостей проекций. Например, на рисунке 3.34. изображена плоскость ABC общего положения, в ко торой выбраны три прямые уровня: h II OXYZ , / // OXYT , q II OXZT . Естественно, что названия горизонтали и фронтали для этого случая неприменимы.
Выбрать в плоскости общего положения прямые уровня относи
тельно плоскостей проекций OXY , OXZ |
и |
ОХТ |
невозможно. |
|
|
|
|||||
|
|
|
По |
расположению |
проек |
||||||
|
ций |
прямых уровня |
/?, |
/ |
и |
q |
|||||
|
можно делать выводы о распо |
||||||||||
|
ложении плоскости |
ABC |
|
отно |
|||||||
|
сительно |
|
|
гиперплоскости |
|||||||
|
OYZT . Дело в том, что по трем |
||||||||||
|
проекциям АХВХСХ, |
А2В2Сг |
и |
||||||||
|
Л,53С3 |
некоторой |
плоскости |
||||||||
|
ЛВС нельзя |
сказать, будет |
ли |
||||||||
|
плоскость |
ABC |
общего |
|
поло |
||||||
|
жения или частного положения |
||||||||||
|
относительно |
гиперплоскости |
|||||||||
|
OYZT . |
Положение |
плоскости |
||||||||
|
ABC |
относительно |
OYZT |
вы |
|||||||
|
ясняется |
только |
после |
по |
|||||||
|
строения ее линий уровня. Так, |
||||||||||
|
если |
после |
|
проведения |
|||||||
Рис. 3.34. Линии уровня в плоскости |
h3 |
II ОХ |
|
окажется, |
|
что |
|||||
h2 |
II ОХ |
, |
hxlt |
ОХ , |
то |
можно |
|||||
общего положения пространства Е4 |
|||||||||||
утверждать, что А ВС ± OZT . |
|||||||||||
|
|||||||||||
Если же окажется, что и /г, // ОХ , то ABC 1 OYZT . И так дапее.
79
