
1671
.pdf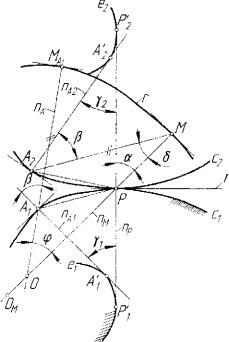
ходящей через полюс |
Р |
и общей |
нормалью пР центроид в точке |
||||
их касания |
- |
полюсе |
Р; |
ух~ пР л пАХ |
и у2 = пР л пЛ2 - углы между |
||
нормалями |
подвижной |
и не |
|
||||
подвижной |
|
|
|
центроид; |
|
||
S — пм л МА2 |
|
|
|
|
и |
|
|
В = МА2 л пА2 |
- |
углы, |
обра |
|
|||
зуемые прямой МА2 |
с норма |
|
|||||
лью пм рулет ты |
и |
нормалью |
|
||||
п,12 подвижной центроиды с2
;<р - пм лпА - угол между бесконечно близко располо женными нормалями рулетты. Отрезок МА2 становится отрезком нормали пл, то есть
МА-, |
- М ААХ, когда центрои |
|||
ды с, |
и с2 касаются в |
точке |
||
АХ=А2. Из геометрической |
||||
схемы |
следуют |
равенства: |
||
<р + в = ух+а, |
а + 5 = |
В + у2. |
||
Оба |
равенства |
дают |
одно: |
|
(р + 5 = ух + у2. |
Введем |
обо |
||
значение: |
As - АХР = А2Р |
- |
Рис. 5.19. Схема определения |
||||||
|
|
|
|
|
|
||||
равные бесконечно малые ду- |
|
кривизны рулетты г |
|
||||||
ги центроид |
с, |
и с2. |
Разделим полученное равенство сумм углов на |
||||||
As |
|
и |
|
перейдем |
|
к |
пределам: |
||
Urn |
lim |
6 |
lim |
Yx + lim -^- = — + - L , где R, и R2 |
• радиусы |
||||
As^oA? |
AS~>O As |
As-+o As |
A< - »D A S R, |
R- |
|
|
|||
кривизны центроид в точке их касания |
Р. Поскольку (р и sin <р - эк |
||||||||
вивалентные |
|
бесконечно |
|
малые, |
то |
можно |
записать |
||
,.Ф .. simp
lim — = |
hm |
|
|
. Заменяя бесконечно малую дугу As стягивающей |
|
|
|||
л*-+о As |
д»->о |
As |
||
|
|
|
140 |
|
се хордой |
и |
рассматривая |
|
треугольник АРАхО, можно записать: |
|||||||
|
|
sine? |
,. |
sm( |
ZOPA,) |
cos а |
„ |
||||
lim |
|
|
— = lim |
|
|
— = |
|
. Поясним полученные равенства. |
|||
|
|
|
|
|
|||||||
•\s->o |
As |
л*н>о |
QAX |
|
POM |
|
|||||
11ервое равенство следует из теоремы синусов для треугольника. Вто
рое равенство следует из того, что |
в пределе секущая АХР занимает |
||||||||||||||||||
положение касательной |
t |
в точке |
Р касания центроид. Угол ZOPAx |
||||||||||||||||
стремится при Д ? - » 0 к углу |
90—а, |
точка |
Л, |
стремиться к точке Р, |
|||||||||||||||
а точка О - к центру Ом |
кривизны рулетты |
г |
в ее точке М . |
|
|
||||||||||||||
Аналогичным |
образом, |
из |
рассмотрения |
АРМА2 |
следует: |
||||||||||||||
S |
,. |
|
|
sin 5 |
,. |
|
sm(ZMPA2) |
cos or |
„ |
_ |
|
|
|||||||
hm —- = |
hm |
|
|
= lim —^ |
|
|
|
— = |
|
|
|
. Таким образом, |
окон- |
||||||
|
|
|
|
|
|
|
|
||||||||||||
Л<!->0 As |
As-»0 |
As |
As->0 |
|
|
MA2 |
|
|
MP |
|
|
|
|
|
|||||
чательно |
|
|
|
полагаем |
|
известную |
формулу |
Эйлера |
[8]: |
||||||||||
cos«( —- |
|
|
h —) = — + |
* |
, |
|
где MP + РОм = RM |
- радиус |
кривизны |
||||||||||
|
|
|
|||||||||||||||||
POfyi |
MP |
Rx |
R2 |
|
|
|
|
|
|
|
|
|
|
||||||
рулетты в ее точке |
М . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В каждый момент времени касания центроид с, и с2 существуют
точки, связанные с подвижной центроидой, рулетты которых имеют нулевую кривизну, то есть для них выполняется условие РОм = =о. Множество таких точек представляет собой окружность, диаметр d которой, на основании формулы Эйлера, удовлетворяет соотношению
— = -- |
+ ^ . Положение точек этой окружности относительно полю- |
|||
d |
Rx |
R2 |
|
|
са |
Р |
определяется отрезком |
PM — d-cosa. Они |
являются точками |
распрямления своих рулетт [8]. |
|
|
||
|
I [усть заданы подвижная с2 |
и неподвижная с, |
центроиды и неко |
|
торая линия а2, жестко связанная с центроидой с2. При качении без скольжения центроиды с2 по центроиде с, линия а2 будет переме щаться, образуя непрерывное однопараметрическое множество линий
{а2}. Огибающей множества {а2 } будет некоторая линия аг, которая по аналогии с траекторией движущейся точки, неизменно связанной
141

с подвижной центроидой с2, может быть названа неподвижной рулеттой, поскольку она неизменно связана с неподвижной центроидой
с,. Если центроиды с2 и с} |
поменять "ролями", то есть считать не |
|||||||||
подвижной с2, а подвижной |
сх, с которой жестко связана линия |
а,, то |
||||||||
в результате |
обкатывания центроиды сх по центроиде с2 получим |
|||||||||
огибающую |
непрерывного |
однопараметрического |
множества |
ли |
||||||
ний |
{а,}, |
которой |
будет линия |
- рулетга а2. Таким |
образом, |
в ис |
||||
ходном положении, когда сх |
и с2 |
суть соответственно неподвижная и |
||||||||
подвижная |
|
центрои |
|
|
|
|
||||
ды, линии ах и а2 бу |
|
|
|
|
||||||
дут |
называться |
со |
|
|
|
|
||||
пряженными, |
то |
есть |
|
|
|
|
||||
взаимоогибаемыми |
|
|
|
|
|
|||||
рулеттами, |
одна |
|
из |
|
|
|
|
|||
которых а{ - непод |
|
|
|
|
||||||
вижная, |
а другая |
а2 |
- |
|
|
|
|
|||
подвижная |
|
рулетты |
|
|
|
|
||||
[81. |
|
|
|
|
|
|
|
|
|
|
|
Пусть |
с |
центрои |
|
|
|
|
|||
дами с, и с2 связаны |
|
|
|
|
||||||
сопряженные |
рулетты |
|
|
|
|
|||||
ах и а2 (рис. 5.20). |
|
|
|
|
||||||
Для |
кривизны непод |
|
|
|
|
|||||
вижной |
рулетты |
а, |
в |
|
|
|
|
|||
ее точке |
М имеет ме |
|
|
|
|
|||||
сто |
вышеприведенная |
|
|
|
|
|||||
формула |
Эйлера, |
ко |
|
|
|
|
||||
торую можно |
преоб |
|
|
|
|
|||||
разовать, |
приняв |
сле |
Рис. 5.20. Построения Бобилье |
|
||||||
дующие |
обозначения: |
|
||||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
142 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
, |
|
|
—i |
|
= —; |
|
= |
= |
; |
|
- — , где |
a |
- диаметр окружно- |
|
R{ |
R2 |
|
d POM |
PMX |
Wj |
|
MP |
m |
|
|
|
сти, состоящей из точек распрямления рулетт. С учетом принятых обозначений формула Эйлера принимает вид (— + —) • cos а- — , из
|
|
|
тх т |
d |
|
тн • d ~ cos ct |
|
||
которого следует формула тх = |
|
|
, в которой параметры тх |
|
|
|
|||
|
т- d -cosor |
|
||
и т связаны дробно - линейным |
соотношением. В |
соответствии с |
||
обозначениями на рисунке 5.20 эти параметры представляют собой длины отрезков тх - РМХ; т = РМ. Таким образом, при неизменных центроидах с, и с2, и неизменном положении прямой пР - общей нормали сопряженных рулетт, проходящей через полюс Р - точку касания центроид с, и с2, точечному ряду {А/}, представляющему собой однопараметрическое множество точек касания всевозможных
рулетт а, и а2 на прямой пг, |
соответствует точечный |
ряд {Мх} |
ряд центров кривизны рулетты |
ах, на той же прямой пР. |
Это соответ |
ствие как раз и определяется вышеприведенными дробно—линейными соотношениями. Из проективной геометрии известно, что в этом слу чае соответствие рядов {м}апг и [ W | } c » P является проективным [10, 37]. Из дробно-линейного соотношения следует, что точка Р яв
ляется |
в этом соответствии двойной, так |
как |
при т = 0 получаем |
т{ = 0 . |
Очевидно, между рядами {M}cznP |
и |
{М2}спР также суще |
ствует проективное соответствие, следовательно, проективное соот ветствие существует и между рядами {Му} и {М2}, и точка Р являет ся двойной, то есть самосоответствснной в проективном соответствии этих рядов. Очевидно, пучок прямых (Fj), проецирующий ряд {М,}, и пучок прямых (Р2), проецирующий ряд {М2}, проективны, по скольку проективны ряды, которые проецируют эти пучки [10, 37]. Поскольку точка Р является двойной в проективном соответствии рядов {Mj} И {М0}, ТО двойной будет и прямая РхР2, соединяющая центры проективных пучков прямых, то есть она соответствует сама
себе. В этом случае, как известно [10, 37], проективные пучки прямых
143

(Р,) и (Р2) перспективны, то есть их соответственные лучи пересе каются в точках на оси перспективы. Из теоремы Бобилье следует, что осью перспективы служит прямая SPA.PM [8]. Из сказанного следует, что центры кривизны центроид с,, с2 и центры кривизны со пряженных рулетт а, и а2 связаны конструктивно простым построе нием Бобилье, которое позволяет при заданных центроидах и одной из рулетт в их контактном положении (М - точка контакта) опреде лить кривизну другой рулетты в ее отсутствие. Например, требуется
определить при |
указанных |
данных |
кривизну рулетты о 2 . Необходи |
|||
мые |
построения |
выполняются в |
следующей |
последовательности: |
||
sLrip, |
P-^MjClx = S, SP2[\nP - M2, |
M2 - искомый центр |
кривизны |
|||
рулетты а2. |
|
|
|
|
|
|
Построение |
Бобилье |
позволяет получить |
известную |
в теории |
||
плоских зубчатых зацеплений формулу Эйлера-Савари. Введем сле
дующие |
обозначения |
|
|
|
|||||
(рис. 5.21): |
\1М. |
Л" - |
|
|
* ^ Л А |
||||
радиус кривизны нспод- |
|
,р |
/ х \ |
||||||
вижной |
рулетты |
а,, |
|
|
/ |
||||
\f.\t • = R" |
- |
радиус |
|
j \ |
/ |
||||
кривизны |
подвижной |
S |
|
|
|||||
рулетты |
а2; |
РМ=т. |
|
|
|||||
|
|
|
|||||||
|
В таком |
случае |
по |
\ |
|
|
|||
лучаем |
РМ2 |
=т + R", |
|
|
|||||
|
|
|
|||||||
РМХ |
= |
R'-m. |
Поскольку |
|
|
|
|||
геометрическая схема на |
|
|
|
||||||
рисунке |
5.21 |
|
отражает |
|
|
|
|||
геометрическую |
карти |
|
|
|
|||||
ну мгновенного |
состоя- |
/ |
\ |
|
|||||
|
|
|
|
|
|
\ |
|
||
ния, |
то |
вполне |
возмож |
|
|
|
|||
ны |
замены |
подвижной |
Рис. 5.21. Схема вывода |
||||||
рулетты |
а2 ее |
центром |
|||||||
уравнения Эйлера-Савари |
|||||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
144 |
|
|
|
кривизны |
М 2 , а неподвижной рулетты |
линией а\, описываемой |
|
центром кривизны М2 при огибании подвижной рулетты а2 |
непод |
||
вижной сг, |
в процессе обкатывания подвижной центроиды с2 |
по не |
|
подвижной |
С ] . В таком случае точка М2 |
может быть принята в каче |
|
стве подвижной точки, неизменно связанной с центроидой с2 и опи сывающей рулетту а\. Применяя на этом основании ранее приведен ную формулу Эйлера, получим:
|
' i |
1 |
|
1 Ч |
1 |
1 |
-и |
1 |
|
|
|
1 |
|
|||
|
cosa( |
|
|
+ |
|
) = — или же —— + |
|
|
|
= |
|
|
. |
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
РМ, |
М~,Р |
d |
R-m |
|
m+R" |
|
|
dcosa |
||||||
Последнее выражение представляет собой известную формулу |
||||||||||||||||
Эйлера-Савари [8]. Очевидно, схема на рисунке |
5.21 позволяет гео |
|||||||||||||||
метрическими построениями определить кривизну рулетга |
а\ в дан |
|||||||||||||||
ной ее |
точке |
М2. |
Последовательность |
построений следующая: |
||||||||||||
s ±РМ2, |
MzP2[)s |
= S, |
SPx0,nP |
= М,, |
М, - |
искомый |
центр |
кривизны |
||||||||
рулетты и\. Рассмотрим пример применения формулы ЭйлераСавари. Предположим, что с, и с2 - неподвижная и подвижная цен троиды радиусов К, и R2 соответственно (рис. 5.22). Проведем через
полюс |
Р |
наклонную прямую |
пР |
под углом а и построим две окруж |
ности |
с |
касающиеся |
этой |
прямой. Для любой точки М е п р |
Рис. 5.22. Сопряженные рулетты цилиндрической зубчатой передачи
построим эвольвенты е{ и е2 окружно стей с'| и с\ соответственно. Пока жем, что эвольвенты ел и е2 могутбыть приняты в качестве сопряженных рулетт, то есть для них выполняется формула Эйлера-Савари. Для элемен тов этой формулы, в соответствии с
рисунками |
5.22, |
можно |
записать: |
|
MM 2 |
=R", |
РМ=т, |
ММХ |
=R'. В та |
ком |
случае |
п о у ч а е м : РМ2 =m + R" = |
||
= P 2 - c o s « ; |
РМ} = R'-m - Rx - c o s а . |
|||
Окончательно, можно записать:
145
i _ + |
|
1 |
|
] _ |
Д |
( 1 , 1 ) = |
1 |
|
Л'-/?г |
|
|
|
|
|
|
|
|
m+R" |
Rycosa R2cosa |
cos a |
Rt R2 |
J cos a |
||||
Этим примером Л. Эйлер в 1767 г. впервые обосновал возможность использования эвольвенты окружности в качестве профилей зубьев цилиндрической прямозубой зубчатой передачи с параллельными осями колес.
5. /. 7. Касание кривых (элементы дифференциальной геометрии)
Довольно часто в результате выполнения теоретического иссле дования либо эксперимента получается массив точек на плоскости и возникает задача проведения линии через упорядоченный массив то чек либо линии через определенные точки с заданными в них допол нительными условиями: положением касательной прямой, значением кривизны и др. Кроме того, иногда требуется заменить заданную ли нию другой линией по определенным условиям замены. Подобные задачи относятся к задачам аппроксимации, то есть когда требуемся заменить одну функцию, заданную массивом точек, графически либо уравнением, другой функцией, удовлетворяющей определенным ус ловиям. Известны следующие основные методы аппроксимации функции [15, 18]:
1. Интерполирование, когда требуется провести кривую через определенные точки исходной кривой;
2. Приближение функций, когда исходная функция на множест ве ее точек заменяется другой функцией с использованием опреде ленного критерия приближения, например, минимизация суммы квадратов отклонений аппроксимирующих и исходных значений
функции: Ziy'i^ Уаппрок)2 = т ' п ;
/=1
3. Построение обвода, представляющего собой составную кри вую, используемую в качестве аппроксимирующей линии, при этом под обводом понимается линия, составленная из дуг кривых одного или различных видов, в точках стыковки которых должен быть вы держан определенный порядок гладкости (порядок касания).
Рассмотрим основные положения теории касания плоских кри вых, известной в дифференциальной геометрии [26] и ее приложениях |8], с точки зрения их практического применения. Пусть имеем две
У |
|
|
|
кривые |
а |
и |
ах |
с |
общей |
точкой |
А0 |
|||||||
|
|
|
(рис. 5.23), уравнения которых следую |
|||||||||||||||
|
|
А,о |
|
|||||||||||||||
|
|
|
щие: |
у |
= f(x) |
- |
для кривой |
а, |
у = |
fx(x) |
||||||||
|
|
|
|
|
||||||||||||||
|
|
|
а, |
|
- для кривой ах. В соответствии с теори |
|||||||||||||
|
|
|
|
ей касания кривых, необходимым и дос |
||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
X |
таточным условием касания не ниже |
п — |
||||||||||||
|
|
|
|
|
||||||||||||||
о |
|
|
|
го |
порядка |
кривых |
а |
и ах |
в их |
общей |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 5.23. Касание кривых |
|
точке |
Ад [х0 |
; у0 |
= Д х 0 ) = fx (х0)] |
являет |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ся совпадение |
производных |
в |
|
этой |
|||||||||
точке: f(x0) |
|
= f\ ( х 0 ) ; / " ( * о ) |
= |
f\ |
(x0); |
..-.fix,) |
= /,"(*„)• |
|
|
|
||||||||
|
Пусть на плоскости задано множество кривых |
(я,}, описываемое |
||||||||||||||||
уравнением |
|
у = fx(x\с,,с2,...,сп). |
На |
|
кривой |
а |
выберем |
|
п |
точек: |
||||||||
Ах, А2,Ап. Подберем значения параметров |
|
сх,с2,...,с„ |
так, |
чтобы |
||||||||||||||
|
|
|
|
|
кривая |
я, множества |
{ах \ проходила че |
|||||||||||
|
|
|
|
|
рез эти п точек (рис. 5.24). Эти значения |
|||||||||||||
|
|
|
|
|
,.(1) |
J2) |
|
|
параметров определяют |
|||||||||
|
|
|
|
|
1 |
' |
2 |
' ., с„ ' |
||||||||||
|
|
|
|
|
ся |
|
из |
|
условий: |
/(х,) = / , (х,), |
||||||||
|
|
|
|
|
f(x2) = fx(x2), |
|
|
|
|
|
f(x„) = |
fl(x„). Вве |
||||||
|
|
|
|
|
дем |
|
в |
|
рассмотрение |
|
функцию |
|||||||
|
|
|
|
|
fi{x) = |
f(x)- |
/, (х). Так как имеют место |
|||||||||||
|
Рис. 5.24. Пересечение |
|
равенства |
|
/л(хх) |
- |
ju(x2) =... = |
fi(xn) |
= 0, |
|||||||||
|
кривых |
|
и |
функция |
/л(х) |
непрерывна на отрезке |
||||||||||||
|
|
|
|
|
||||||||||||||
[хх, хп] и дифференцируема в каждой внутренней точке этого отрезка,
поскольку эти условия выполняются для каждой из функций / ( х ) |
и |
|||||||
/ ( х , ) , |
то |
по |
теореме |
Ролля о |
корнях |
производной |
получим: |
|
|
|
,0) |
|
(0 |
где |
Х^ ^ Х-^ |
_Х"2 *С Х^ |
*^ |
|
|
|
|
|
||||
<...<х„ |
< |
х„ |
Применив |
теорему |
Ролля для |
функции / / ( х ) , полу- |
||
146 |
147 |
|
чим: |
M"(xi2)) = м"(х?)) = -=М"(х<1%) = °> |
гДе |
Х?У |
<*\2) |
< х 2 ° < |
|||||
< х[2) |
<...< х(2}2 < х л - 1 - |
И |
так |
далее. |
В |
итоге |
получаем: |
|||
^С-').(*(»-')) = 0> |
Где |
x1(и-2)<JcI(и-1)<xfл•^,. |
Устремим |
все |
точки |
|||||
/4,, Л 2 , к р и в о й |
а |
к ее точке |
А0(х0), то есть выполним предель |
|||||||
ный переход lim JC, |
= lim х2 |
- ... — lim хп - х0. В этом случае параметры |
||||||||
с\]\с21\...,с^ |
будут |
стремиться к |
своим предельным |
значениям |
||||||
с1(0),с2°\...,ся0) |
. В итоге отрезок |
со всеми |
своими точками бу |
|||||||
дет стягиваться в точку х0. В пределе для всех вышеприведенных
производных |
/и'(х), |
fi"(x), |
fj"~l{x) получим: |
fj'(x(]) = /j"(x0) = |
|
= ... - ju"~](x0), |
что |
соответствует |
необходимому |
и |
достаточному ус |
ловию касания не ниже (п -1)—го порядка кривых |
а |
и я , , также при |
|||
веденному выше. Из вышеизложенного следует важный результат о том, что две алгебраические кривые порядков тип могут иметь ме жду собой касание не выше ( W - W - I ) - J O порядка, поскольку по тео
реме Безу они пересекаются в (т-п) точках |
и, следовательно, любая |
из них может проходить не больше чем через |
{т-п) бесконечно близ |
ко расположенных точек другой. |
|
Рассмотрим примеры. |
|
1. Соприкасающаяся прямая. Пусть имеем прямую общего по |
|
ложения относительно декартовой системы |
координат в плоскости: |
у - с,х + с2. Так как п = 2, то соприкасающаяся прямая может иметь с |
|
кривой касание не ниже первого порядка. Прямая является касатель
ной к кривой у- f(x) в некоторой ее точке (х0,>>0). Действительно. с,х0 + с 2 - уп = f(x0); у'„ = Г (*о) = с\; с г = У о _ У'о 'хо • Таким обра
зом, получаем: у - у0'(х~ х0) + у0. Очевидно, что имеет |
место усло |
вие у"- О для рассматриваемой прямой. Точки кривой у |
- /(х), в ко |
торых / " ( х ) = 0, называются точками распрямления. В этих точках касательная к кривой проходит через три бесконечно близкие точки.
2.Соприкасающаяся окружность. Из уравнения окружности
(х-a)2 +(y-b)2 -R2 = 0 следует, что и = 3. Поэтому окружность с
148
кривой y~f(x) может иметь касание не ниже второго порядка. Из уравнения окружности можно получить последовательным диффс-
реш 1ированием |
следующие |
уравнения: |
(у~Ь)- у'+(х - а) = 0; |
|||||
(у - И) • .У"+(У )2 |
+ 1 = 0 . По приведенным выше необходимым и дос- |
|||||||
I аточным условиям касания не ниже (и - 1)-го порядка кривых в точ |
||||||||
ке |
(х0,У0) |
принимаем |
у = |
Дх0); у'=/'(х0); |
/ ' = / " ( > „ ) , |
где |
||
v |
= f(x) - уравнение некоторой |
кривой. Из |
трех |
приведенных |
урав |
|||
нений для окружности и |
уравнения кривой |
у = f(x) следуют уравне |
||||||
ния трех параметров окружности, соприкасающейся с кривой в точке
|
|
[] + ( y ) |
2 l v |
i + (V) |
2 |
„ |
[i + (/)2 ]3/2 |
„ |
|||
(x0,yQ): a = x- 1 |
|
КУ , |
1 |
• |
; в = у + —V -; |
R |
= |
.. |
' Если |
||
|
|
|
V |
|
|
У |
|
|
У |
|
|
у= f"(xn) = 0, |
то |
искомой |
окружности |
в |
точке |
(х0,у0) |
кривой |
||||
V = / ( х ) не |
существует, |
поскольку эта точка - точка распрямления |
|||||||||
кривой. |
|
|
|
|
|
|
|
|
|
|
|
Эти уравнения совпадают с известными уравнениями, опреде ляющими окружность кривизны кривой в некоторой ее точке (л\у). Таким образом, соприкасающаяся окружность является окружностью кривизны кривой линии. С другими кривыми второго порядка окруж ность пересекается в четырех действительных точках. Следовательно, на основании сделанного выше вывода о касании двух алгебраиче ских кривых, она не может иметь с ними касание выше третьего по рядка. В вершинах кривых второго порядка, в которых их кривизна достигает экстремума, соприкасающаяся окружность имеет касание третьего порядка, то есть она проходит через четыре бесконечно близко расположенные точки этих кривых.
3. Соприкасающаяся парабола. Пусть задана парабола с осью, параллельной оси OY: у = с, + с2х + с3х2. Очевидно, что /7 = 3. Сле довательно, такая парабола может иметь с кривой у - f(x) касание
не ниже второго порядка. Из уравнения параболы, соприкасающейся с кривой _у = f(x) в точке (х0,у0) можно получить следующие урав-
149

нения для определения коэффициентов: /(х 0 ) = с} +с2х0 +с 3 х 2 ;
f'(xQ) = с2 + 2с3х0; / " ( * 0 ) = 2с3 .
4.Соприкасающийся эллипс. Для эллипса с осями, параллель-
, х - с ,2 ,j-tf\-> .
ными координатным |
осям, |
можно записать: ( |
|
) + ( - |
) " = 1 , |
||||
|
|
|
|
|
|
|
a |
|
b |
2 |
2 |
2 |
2 |
2 |
2 |
|
|
|
|
Z> |
(х - с) |
+ а |
(у - d) |
-а Ъ |
|
= О. Согласно последнему уравнению |
|||
следует л = 4. Поэтому, такой эллипс может иметь соприкосновение с кривой у = f (х) не ниже третьего порядка. Трижды дифференцируя
последнее уравнение эллипса, получим следующие уравнения:
а2(у - d) • y'+b2(x - с) = 0; а2(у - d) • у"+а2 • (у1)2 + Ь2 = 0;
0>-</)-У"+зуУ'=о.
Из этих уравнений, с учетом исходного уравнения соприкасаю щегося эллипса, могут быть получены его параметры а, Ь, с, d.
Аналогичным образом, как и в случае эллипса, может быть рас смотрена соприкасающаяся с кривой у — f (х) гипербола с осями, па
раллельными координатным осям, |
описываемая уравнением |
||||
, х |
~ с \ 2 |
/ > ' ~ ^ ч 2 |
, |
|
|
( |
_ ^ |
|
) |
= 1, и найдены, в результате трижды выполняемого |
|
|
|||||
|
a |
b |
|
|
|
дифференцирования, се параметры а, Ь, |
с, d. |
||||
5.1.8.Конструирования обводов из дуг кривых второго порядка
Известно множество способов конструирования обводов точек на плоскости. Основными из них, п о у ч и в ш и м и наибольшее практиче ское применение, являются [16]:
1. Радиусографический, когда через упорядоченный массив то чек проводится обвод первого порядка гладкости, состоящий из дуг окружностей разных радиусов, имеющих в точках стыка общие каса тельные;
2. Способ кривых второго порядка, когда обвод составлен из дуг кривых второго порядка, имеющих в точках стыка общие касательные
150
(обвод первого порядка гладкости) или равные значения кривизны (обвод второго порядка гладкости);
3.Сплайн - аппроксимация.
Доказано, что ось изогнутой гибкой тонкой линейки (spline), про ходящей через заданные точки, описывается полиномом третьей сте пени у = аа + ахх + а2х2 + а,х3, представляющем уравнение кубиче ской параболы. Эта парабола может быть задана: четырьмя точками, двумя точками и касательными в них. Обвод первого и второго по рядков гладкости составляется из дуг кубических парабол. Если, на пример, заданы две точки (хг,у,) и (xi+x,yi+x), и две касательные в них (у))'х и (у,-,,)',, то этими условиями, согласно уравнению кубиче ской параболы, могут быть определены четыре коэффициента в урав нении кубической параболы. Дуга полученной параболы пройдет че
рез эти две точки с касательными к параболе в них [18]. |
|
|||
|
Рассмотрим теоретические |
|||
|
положения, составляющие осно |
|||
|
ву конструирования |
обводов из |
||
|
дуг кривых второго порядка. Как |
|||
|
известно, кривая второго поряд |
|||
|
ка (коника) определяется зада- |
|||
|
нием в плоскости пяти точек |
|||
|
A,B,C,D,E |
общего |
положения |
|
Рис. 5.25. Касательный треугольник |
(рис. 5.25). Если две точки кони- |
|||
ки, например, D и Е, устремит ь |
||||
2 |
||||
коники к
каждую к соответствующей точ
ке: D—>С, то предельным положением секущей ЕА станет касательная tA в точке А, а секущей DC - касательная tc в точке С
коники. Получаем переход от задания коники пятью точками к ее за данию тремя точками и двумя касательными в них. Образующийся треугольник FAC называется касательным треугольником коники. Этот треугольник положен в основу известного способа инженерного дискриминанта, применяемого для конструирования обвода первого порядка гладкости из дуг коник [15]. Предположим, задан ряд точек
151

А,С, D, Е,... и положения касательных tA,tc,tD,th,. в них (рис. 5.26). Требуется провести через эти точки указанный обвод. Ес
ли в касательном треугольнике AFC провести медиану FB' и вы
брать на ней некоторую точку В, то в зависимости от значения отно
шения |
ВВ': |
FB=d получим различные возможности для проведения |
|||||
дуги |
ABC коники: |
d = 0,5 |
- дуга параболы к{, d > 0,5 - дуга гипер |
||||
болы |
к2, |
d < 0,5 |
- |
|
|||
дуга |
|
эллипса |
к2. |
/л |
|||
Выбрав одно из трех д? |
^ |
||||||
возможных значений |
|
||||||
инженерного |
|
дис |
|
||||
криминанта |
|
d, |
по |
|
|||
лучим |
определенную |
|
|||||
точку |
В на |
медиане |
|
||||
FB' |
и, |
следователь |
|
||||
но, |
дугу определен |
|
|||||
ной |
коники |
кг, |
оп- |
Рие. 5.26. Обвод первого порядка иадкости |
|||
|
|
|
|
|
|
|
|
ределяемои |
|
усло |
из дуг коник |
||||
виями: |
A,tA; |
B;C,tc. |
|
||||
После проведения касательной tB, параллельной стороне АС, полу
чаем новую пару касательных треугольников AF{B и BF2C. В каж
дом из них выполняются построения, подобные построениям точки В в треугольнике AFC. Для треугольника AF{B это будет точка #, . Последующие проведения касательных через полученные точки В:
коники к2 внутри треугольников указанной пары (например, tm II АВ
) приводит к образованию новых четырех касательных треугольников и т.д. Описанный процесс конструирования дуги коники к2 продол жается до получения требуемого числа ее точек. Затем выполняется по описанному алгоритму построение дуги коники к\ и дуги коники
к\. Очевидно, сконструированный обвод из дуг коник к2, к2, к2
представляет собой обвод первого порядка гладкости.
152
Зададим следующий аппарат отображения (проецирования) про
странства Е3 (рис. 5.27): |
|
|
|
|
|
|
|
|
1. |
Центры проецирования 5 и S"x |
(несобственный); |
|
|||||
2. |
Плоскость проекции Я, . |
|
|
|
|
|
||
Плоскость А пространства при таком |
аппарате проецирования |
|||||||
будет |
моделироваться |
на |
плоскости |
проекций |
Пх |
гомологией |
||
( £ , , « , , 4 |
<-> А'\), где Sx |
- неизменный для всех |
плоскостей А про |
|||||
странства центр гомологии, |
sx - ось гомологии, |
А] |
о А'\ |
- пара со |
||||
ответственных точек, моделирующая точку |
Ае А. |
Пусть |
плоскости |
|||||
Апринадлежит некоторая линия к . Очевидно, линии kt и к'\ в
плоскости Я,, полученные проецированием линии |
к |
из центров S и |
|||||||||||||
5 " ^ |
соответственно, будут гомологично соответственны. В |
итоге ли |
|||||||||||||
ния |
к |
может моделироваться на плоскости проекций |
Я, следующи |
||||||||||||
ми способами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1. |
Одной проекцией |
или |
к", и гомологией |
(S,,^,/!, о Л", ), |
||||||||||
|
|
|
|
|
|
где |
Ах |
о Л", |
- |
|
модель |
любой |
|||
|
|
'~^"\ |
|
|
|
точки плоскости |
А |
в указанной |
|||||||
|
|
|
|
|
|
гомологии. |
|
|
|
|
|
|
|
||
|
|
54 |
^ |
21 |
|
|
2. |
Одной проекцией А, или |
|||||||
|
|
|
к'\ |
и |
тремя |
парами |
проекций |
||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Ах «-» /4",, |
#j <н> |
|
|
С, |
<->Г", |
||||
|
|
|
|
|
|
трех различных |
точек |
А, В и С |
|||||||
|
|
|
|
|
|
плоскости А . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Очевидно, |
при |
неизменном |
||||||
|
|
|
|
|
|
центре |
5, |
|
гомологии |
модель |
|||||
|
|
|
|
|
|
любой |
плоскости |
пространства |
|||||||
|
|
|
|
|
|
будет определена |
заданием оси |
||||||||
Рис. 5.27. Моделирование плоскости |
гомологии |
s, |
и пары гомологич- |
||||||||||||
|
|
пространства гомологией |
|
ных точек в плоскости Я, . |
|||||||||||
|
|
|
|
|
|
||||||||||
153
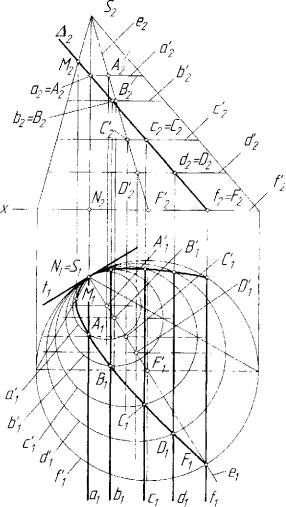
Рассмотрим эллиптический конус второго порядка, у которого одно из двух семейств окружностей таково, что плоскости окружно стей этого семейства перпендикулярны одной образующей SN(S1NUS21V2) этого конуса (рис. 5.28). Если расположить этот ко-
Рис. 5.28. Пучок гомологии с инвариантными центром 5 и коникой к2
пус |
относительно |
плоскости проекций 77, так, чтобы выполнялось |
|||
условие SN L 7/,, |
то |
указанное семейство |
окружностей |
отобразится |
|
на |
плоскость 77, |
в |
пучок окружностей, |
проходящих |
через точку |
.V, = 5 ) с общей касательной t{. Проведем некоторую проецирующую плоскость A А. П2, пересекающую рассматриваемый конус. Очевид но, что линией пересечения будет некоторая коника к2(к2,к2). Ее ор тогональная проекция к2 также будет коникой, поскольку при орто гональном проецировании в общем случае порядок алгебраической кривой и порядок ее проекции равны. Коника к2 пересекает каждую окружность а\ , в\ , с\ , d\ , f\ , ... пучка окружностей в четырех точ ках: одной двойной (гонка касания S{ с общей касательной tx) и двух простых точках. Прямые, соединяющие пары простых точек пересе чения, образуют пучок параллельных прямых а, II вх II с, II dx II /,
поскольку каждая из этих прямых представляет собой ортогональную проекцию линии пересечения плоскости А и плоскости из пучка па раллельных плоскостей, которым принадлежат окружности рассмат риваемого семейства на конусе. Очевидно, каждая из окружностей
а'(а\ ,а\ ),b'(b\ ,b'2),... может быть рассмотрена как центральная проекция коники к2(к2,к2) на плоскость этой окружности из центра
S(S],S7), а сама коника к2(к2,к2_) может быть рассмотрена как цен
тральная проекция каждой из этих окружностей на плоскость А ко ники к2.
На плоскости 77, получаем пучок гомологии с инвариантным центром 5, и инвариантной коникой к2 с параллельными осями го мологии а,, в,, с,, dx, fx, ... В каждой гомологии образом соответст вующей окружности является одна и та же коника кх . Ось гомологии проходит через точки пересечении этой окружности и коники к2. Для предельной окружности а\ пучка окружностей, то есть для окружно
154 |
го |

сти кривизны коники кх , ось гомологии ах проходит через центр S, - точку касания коники к2 и всех окружностей пучка.
Таким образом, анализ вышеизложенных построений позволяет утверждать о том, что каждая из окружностей, соприкасающихся с коникой в одной и той же точке, гомологична этой конике; точка ка сания есть центр гомологии; оси пучка гомологии образуют пучок па
раллельных прямых. Это особенное |
гомологичное |
свойство коники |
к2 известно в теории обводов точек |
на плоскости |
[18], но здесь оно |
получено не из косвенных, а из прямых, более простых и наглядных рассуждений.
Рассмотрим применение гомологичного свойства коники к2 для построений дуг коник, используемых при конструировании обводов первого и второго порядков гладкости. Предположим, что заданы точки S,A и В коники к2 и ее касательные ts и tA (рис. 5.29). Требу
ется |
построить |
конику. |
Ясно, |
|
|
|
|
||||||
что |
этих |
условий |
достаточно |
|
|
|
|
||||||
для построения коники к . Из |
|
|
|
|
|||||||||
вестны |
решения рассматривае |
|
|
|
|
||||||||
мой задачи, например, решение, |
|
|
|
|
|||||||||
основанное |
на |
проективном |
|
|
|
|
|||||||
подходе |
[37]. Применим |
гомо |
|
|
|
|
|||||||
логичное |
свойство |
коники |
для |
|
|
|
|
||||||
решения |
рассматриваемой зада |
|
|
|
|
||||||||
чи. |
Проведем |
окружность |
d |
|
|
|
|
||||||
произвольного |
радиуса, |
сопри |
|
|
|
|
|||||||
касающуюся с |
коникой в точке |
Рис. 5.29. Построение коники к" на |
|||||||||||
S. |
Очевидно, |
|
точка |
S |
может |
||||||||
|
основе соприкасающейся окружности |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
быть принята в качестве центра |
|
|
|
|
|||||||||
гомологии. Определим |
ось |
гомологии |
а. |
Для |
этих целей построим |
||||||||
точки |
A'-SAf]a' |
и |
В'- |
SBf]a', представляющие |
собой образы точек |
||||||||
А е к2 и |
В е к2 |
в гомологии. Прямые |
АВ |
и А'В* определяют первую |
|||||||||
|
|
|
|
|
|
|
|
|
|
156 |
|
|
|
точку |
ТАВ оси а |
гомологии: ТАВ = ABf] А' В'. Проведем касательную |
|||
t'л в |
точке |
А'еа'. |
Точка |
пересечения касательных TA=tAf)t'A пред |
|
ставляет собой вторую точку оси |
а гомологии. Действительно. При |
||||
стремлении точки |
В к точке А |
по конике к2, точка В' будет стрс- |
|||
миться к точке А' |
по окружности |
а', поскольку в пределе прямая го |
|||
мологичного |
соответствия |
ВВ' совпадает с прямой гомологичного |
|||
соответствия |
АЛ', |
а хорды |
АВ коники и А'В' окружности станут ка |
||
сательными |
tA и fА. Поэтому касательные в соответственных в гомо |
||||
логии точках коники и окружности пересекаются в точке на оси го мологии. Таким образом, гомология определена центром S, осью а и парой соответственных точек В и В' или А и А'. Задание гомоло гии и окружности а' позволяет построить ее образ к2, который явля ется искомой коникой.
Если в условии рассматриваемой задачи вместо точки В ввести значение кривизны конструируемой коники в се точке S, то для кон струирования коники необходимо провести окружность кривизны а'0
в точке |
S. Поскольку в этом случае ось гомологии а0 проходит через |
|||
|
центр S, то для построения еще |
|||
|
одной ее точки достаточно опреде |
|||
|
лить |
точку пересечения |
касатель |
|
|
ных tA и t'A в соответственных |
|||
|
точках коники и окружности кри |
|||
|
визны йг'0. Задание центра S гомо |
|||
|
логии, |
оси гомологии |
S еа0, ок |
|
|
ружности кривизны а'0 в точке S |
|||
|
коники и точки А этой коники по |
|||
|
зволяет построить по этим услови |
|||
|
ям конику к2 с заданной кривиз |
|||
|
ной в ее начальной точке S. |
|||
а |
а' |
Из |
анализа вышерассмотрен- |
|
|
ной геометрической схемы образо |
|||
Рис. 5.30. Определение окружности
вания пучка гомологии на плоско-
кривизны коники
157
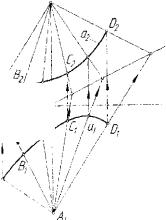
сти Я, (рис. 5.28) следует, что если провести jry4 из центра 5,, пере
секающий окружности пучка, то касательные к окружностям пучка, проведенные в точках их пересечения с этим лучом, будут параллель ными. Это свойство касательных позволяет получить решение сле
дующей задачи. Пусть заданы три точки S, В, А коники и касатель ные ts и tA к ней в точках S и А (рис. 5.30). Требуется определить кривизну коники в ее точке S. Для решения задачи построим произ
вольную окружность d из пучка окружностей с общей точкой S и
касательной |
ts в ней. В соответствии с решением предыдущей задачи |
||||||
(рис. 5.29), построим ось а |
гомологии с центром S, в которой обра |
||||||
зом |
окружности а' |
будет |
коника к2, |
определяемая |
условиями: |
||
S,ts;A ЛА; В. |
Проведем |
ось |
as |
другой |
гомологии по |
условиям: |
|
as//a; |
Seas. |
В новой гомологии |
с центром S и осью |
as образом |
|||
искомой окружности а'а кривизны будет та же коника к2. Дальней
шие построения выполняются в следующей последовательности:
/%П% -Tv: Ts er',,,, t\0!it'4 (по свойству касательных окружностей
щчка. провод.-:? кых в точках пересечения этих окружностей с лучом,
выходящим |
из их |
обшей точки |
касания |
S); |
SAC\t\0 = А'0; |
n'Qf)ns = 0'п, |
где п'0 - срединный перпендикуляр отрезка SA'0, ns - |
||||
нормальная |
прямая (ns |
lts,SeNS). Таким |
образом, |
точка |
О',, - иско |
мый центр окружности кривизны а\, коники к2 в ее точке S .
Эта и предыдущая рассмотренные задачи могут быть положены в основу конструирования обвода второго порядка i ладкостн из дуг ко ник с общим значением кривизны в точках их стыка.
Множественные теоретические аспекты и нюансы различных ал горитмов конструирования обводов различных порядков гладкости из дуг коник и других плоских кривых, а также аналитическое описание сплайн-аппроксимации и сплайн-интерполяции можно найти в рабо тах [16, 18].
5.1.9. Моделирование плоской кривой па чертеже Монжа
В общем случае моделирование плоской кривой линии, принад лежащей плоскости общего положения, основано на модели этой
плоскости, которая на чертеже Монжа представляет собой |
родство. |
|||||||||||||||||
|
|
|
|
|
|
|
А |
|
Тогда |
пара |
|
ортогональных |
||||||
|
|
|
|
|
|
|
|
|
|
проекций |
|
плоской |
кривой |
|||||
|
|
|
|
|
|
|
|
|
|
линии |
на |
чертеже |
Монжа |
|||||
|
|
|
|
|
|
|
|
|
|
d может |
быть |
рассмотрена |
как |
|||||
|
|
|
|
|
|
|
|
|
|
два точечных |
ряда, |
соответ |
||||||
|
п, |
/ |
|
|
|
|
|
|
|
ственных |
в этом родстве. За |
|||||||
|
|
|
|
|
|
|
|
|||||||||||
X |
|
|
|
|
|
|
|
дание |
одной |
проекции |
at |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
п, / |
|
|
< |
|
|
|
|
|
плоской |
кривой |
и |
задание |
||||||
|
/ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
родства |
(d,A{<+A2), моде |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
лирующего |
плоскость |
этой |
||||||
|
|
|
|
|
|
|
|
|
|
кривой, позволяет |
построить |
|||||||
|
|
|
|
|
|
|
|
|
|
вторую проекцию а2 кривой |
||||||||
|
|
|
|
|
|
|
|
|
|
(рис. 5.31). Таким образом, |
||||||||
|
Рис. 5.31. Модель плоской кривой |
плоская |
линия пространства |
|||||||||||||||
|
|
|
|
на чертеже Монжа |
|
может |
|
моделироваться |
на |
|||||||||
чертеже Монжа следующим образом: |
|
|
|
|
|
|
|
|
||||||||||
|
1. |
Родством, моделирующем плоскость этой кривой, и одной из |
||||||||||||||||
проекций а, или а2; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
2. |
Одной проекцией а, |
или а2 |
и тремя парами соответственных |
||||||||||||||
в |
родстве, |
моделирующем |
плоскость |
кривой, |
точек, |
например: |
||||||||||||
Я, +>В2, В, |
е а , , В2еа2; С, |
<-»С2, |
Схеа{, |
С2еа2; |
D, |
f > D 2 , |
D, |
е о, |
||||||||||
, |
D2 е а2. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5.2.Пространственные кривые
Вучебных изданиях по начертательной геометрии пространст венным кривым линиям уделяется незначительной внимание. Исклю чение составляет учебник [2]. Очевидно, это связано с тем, что тради-
158 |
159 |
|
