
1671
.pdf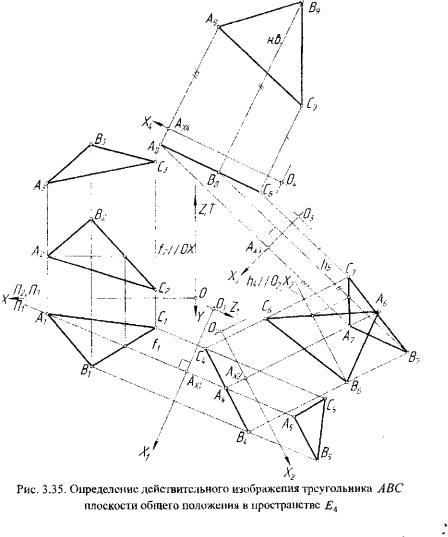
|
3.5.2. |
Определение |
действительного |
|
|
|
|
||||||
|
|
изображения |
треугольника |
ABC |
|
|
|
|
|||||
Определение действительного |
изображения |
треугольника |
ABC |
- |
|||||||||
это задача по преобразованию плоскости общего положения |
ABC |
в |
|||||||||||
частное положение. |
|
|
|
|
|
|
|
|
|
|
|
||
Пусть задана |
плоскость |
ABC общего положения. Это означает, |
|||||||||||
что, например, h3 |
II ОХ |
, |
h,J ОХ , |
hxHOX |
или |
/ 3 # ОХ , |
/2//ОХ |
, |
|||||
/, i ОХ |
или q3# ОХ , q2# ОХ, |
qxll ОХ • Выберем любую из этих ли |
|||||||||||
ний уровня. На рисунке 3.35 выбрана линия /2 // ОХ |
и построена /,. |
||||||||||||
Можно было построить |
/3 |
и вести все построения относительно нее. |
|||||||||||
Выбрана новая гиперплоскость проекций oxXxZT |
, при этом ось ОХ, |
||||||||||||
принадлежит плоскости OXY . На гиперплоскости проекций построе |
|||||||||||||
ны проекции Л4£4 С4 и А5В5С5, причем А.ХВЛС,Х |
- вырожденная про |
||||||||||||
екция. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем выбрана гиперплоскость проекций |
02X2ZT |
, параллельная |
|
||||||||||
плоскости ЛВС. На чертеже |
это означаетвыбор оси ОгХ2 // Л4Я4С4. |
||||||||||||
Построены проекции АЛВ6Св |
и Л7В7С-,. Поскольку |
ABC И ()2Х 2ZT , то |
|||||||||||
на эту |
гиперплоскость |
треугольник ABC проецируется в |
"натураль |
||||||||||
ную |
величину". |
Другими |
словами, |
плоскость |
ЛВС в |
системе |
|||||||
02X2YZT является |
плоскостью |
уровня. |
Таким образом, |
произошло |
|||||||||
понижение размерности пространства, в котором расположена плос
кость ABC. Теперь можно считать, |
что треугольник ABC |
расположен |
в трехмерном пространстве и его |
проекции есть А6ВЬСЬ |
и Л7 #7 С7 . |
Дальнейшие построения такие же, как и в трехмерном пространстве. Окончательно получаем проекцию A9BqCq, которая представляет со бой действительное изображение треугольника ABC.
В зависимости от выбора прямой уровня можно реализовать шесть направлений решения задачи. Во всех из них будет получено одно и то же действительное изображение треугольника ABC.
На рисунке 3.35 выбор осей ОхХх, ОгХ2, 03Х3, 0,Х_Х диктует ся направлением линий /,, Л4В4С4, А5, Л8#8С8. Расстояния, отклады ваемые от осей OiXi следующие: l-^^nj = ИгЛт!' j^s^xi! = ИзДг|>
= |.47 4гз|. Аналогично, для точек Вх...., В9 и С,,..., С9.
80 |
81 |
3.6.Моделирование гиперплоскостей пространства Еп
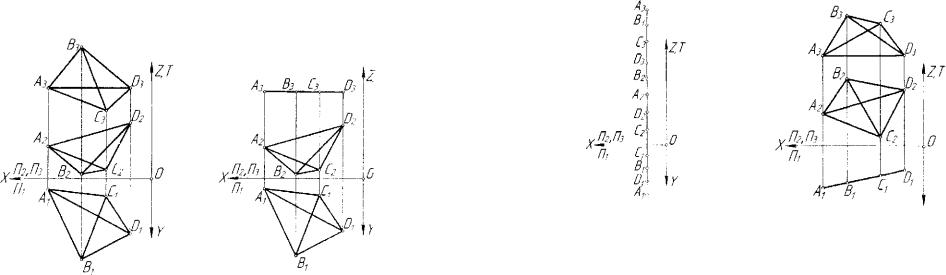
Гиперплоскость (3-плоскость) пространства Еп определяется че тырьмя параметрами или задается четырьмя независимыми точками пространства. Пусть это будут точки A,B,C,D . Тогда на простейшей модели будут проекции (AUA2,A2), (S,,B2, В3 ), (С1 5 С2 ,С3 ) и (£>,.D2 ,£>3 ) (рис. 3.36). От этого задания можно перейти к другому
Рис. 3.36. Модель гиперплоскости |
Рис. 3.37. Гиперплоскость уровня |
||
относительно гиперплоскости |
|||
пространства |
Ел |
||
OXYZ пространства Е4 |
|||
|
|
||
заданию гиперплоскости, например, двумя скрещивающимися пря мыми - ребрами тетраэдра ABCD , плоскостью и точкой - гранью и противоположной вершиной тетраэдра ABCD , плоскостью и пересе кающей ее прямой, тремя прямыми, пересекающимися в одной точке и т.д.
Судя по чертежу, можно утверждать, что гиперплоскость ABCD является гиперплоскостью общего положения по отношению к гипер
плоскостям проекций |
OXYZ , |
OXYT , |
OXZT , но ничего определенно |
||
го нельзя сказать о ее положении |
относительно |
гиперплоскости |
|||
OYZT . |
|
|
|
|
|
Гиперплоскость |
ABCD |
частного |
положения может быть |
парал |
|
лельна одной из |
гиперплоскостей |
проекций. |
Например, |
если |
|
/ 4 = tB |
= tc = tD |
= сош7 , то гиперплоскость ABCD будет параллельна |
|
гиперплоскости |
OXYZ (рис. |
3.37). Такая гиперплоскость называется |
|
гиперплоскостью уровня. |
|
||
На |
рисунке |
3.38 приведена модель гиперплоскости уровня |
|
(ABCD )// OYZT, для которой |
хА = хв = хс = xD = const. |
||
|
Y |
Рис. 3.38. Гиперплоскость уровня |
Рис. 3.39. Проецирующая относительно |
относительно гиперплоскости |
OXY гиперплоскость |
|
|
OYZT пространства ЕА |
пространства |
|
Гиперплоскость может быть перпендикулярна какой-либо плос кости проекций. Тогда на этой плоскости проекций проекция гиперп лоскости будет вырожденной. На рисунке 3.39 показана гиперпло скость ABCD , перпендикулярная плоскости OXY . Такая гиперпло скость называется проецирующей относительно плоскости OXY . Аналогично будут выглядеть модели проецирующих гиперплоскостей относительно других плоскостей проекций.
Следует заметить, что невырожденными проекциями гиперпло скости будут все поля проекций OXZ , OXY (рис. 3.37) и ОХТ, OXZ (рис. 3.39).
3.6.1. Принадлежность точки, прямой и плоскости гиперплоскости
Можно сформулировать следующие признаки принадлежности:
83
82
1) точка принадлежит гиперплоскости, если она принадлежит какой-либо линии данной гиперплоскости;
2)точка принадлежит гиперплоскости, если она принадлежит какой-либо плоскости данной гиперплоскости;
3)прямая принадлежит гиперплоскости, если две ее точки при надлежат данной гиперплоскости;
4)плоскость принадлежит гиперплоскости, если три ее точки, не лежащие на одной прямой, принадлежат данной гиперплоскости.
Очевидно, что для рисунков 3.37, 3.38, 3.39 задача о принадлеж
ности точки данной гиперплоскости частного положения решается
просто, без дополнительных построений. Так на |
рисунке 3.37 доста |
||||||||||||
точно, |
чтобы |
проекция |
|
Е3 |
точки Е(Е},Е2,Е3) |
принадлежала пря |
|||||||
мой A3B3C3D3. |
Тогда Е е (ABCD). То же самое относится к гиперп |
||||||||||||
лоскости, |
изображенной |
|
на |
рисунке 3.39. Если E]sA]B,ClDl, то |
|||||||||
Е(ЕХ,Е2,Е3) е (ABCD ). |
|
|
|
|
|
||||||||
|
Рассмотрим |
эту |
задачу |
в |
|
|
|||||||
общем случае. Пусть дана ги |
|
|
|||||||||||
перплоскость ABCD (рис. 3.40). |
|
|
|||||||||||
Пусть |
|
будет' |
|
дана |
|
точка |
|
|
|||||
Е{Е,,Е2.Е3), относительно ко |
|
|
|||||||||||
торой нельзя сказать ничего оп |
|
|
|||||||||||
ределенного |
по принадлежности |
|
|
||||||||||
ее |
данной |
|
гиперплоскости. |
|
|
||||||||
Предположим, |
что |
существует |
|
|
|||||||||
точка F(F},F2), |
принадлежащая |
|
|
||||||||||
данной |
гиперплоскости и |
кон |
|
|
|||||||||
курирующая |
с |
Е |
относительно |
|
|
||||||||
плоскостей OXY |
и OXZ . Тогда |
|
|
||||||||||
по |
условию |
принадлежности, |
|
|
|||||||||
можно построить точку F, - |
|
|
|||||||||||
проекцию точки |
F |
на |
|
плос |
|
|
|||||||
кость |
ОХТ. |
Если |
F3 |
Е3, |
то |
|
|
||||||
Е е |
(ABCD), |
если |
F3 * |
£ |
то |
|
|
||||||
Ег(ABCD). |
|
|
|
|
|
|
|
|
|
|
|||
|
Для |
реализации |
этой |
идеи |
Рис. 3.40. Принадлежность точки |
||||||||
проведем |
через |
точку |
Е |
гипер |
|||||||||
гиперплоскости пространства £4 |
|||||||||||||
плоскость А, |
перпендикулярную |
||||||||||||
|
|
||||||||||||
84
плоскости OXY . Это можно сделать бесконечным числом способов. На рисунке 3.40 гиперплоскость Л(4) проведена через точку А . Пе ресечение ABCD и А будет плоскость, которую можно построить по трем точкам А, М, iV, где М е ВС, N е BD . Таким образом, полу чаем Аг = (A2M2N2), Аъ = (/i3M3JV3). Очевидно, что размерность по нижена до трех, и мы получили задачу на принадлежность точки E(E]tE2) плоскости A(A2M2N2>A3M3N3). Дальнейшее решение было описано выше.
На рисунке 3.40 Е3 * Е3, следовательно, Е е (ABCD).
Для решения задачи о принадлежности прямой и плоскости дан ной гиперплоскости необходимо описанный алгоритм повторить два и три раза, соответственно.
3.6.2. Прямые уровня и плоскости уровня
вданной гиперплоскости
Вданной гиперплоскости общего положения ABCD MOiyr быть выбраны прямые, параллельные какой-либо гиперплоскости ироек-
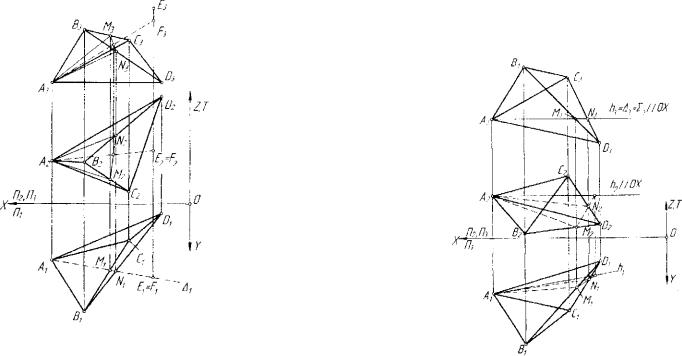
Рис. 3.41. Прямая уровня гиперплоскости относительно плоскости OXY пространства £4
85

ций, и прямые, параллельные какой-либо плоскости проекций. На ри сунке 3.41 изображена прямая h(h„k2,h3) данной гиперплоскости, параллельная плоскости OXY , а на рисунке 3.42 - прямая h(hx,h2,h3) данной гиперплоскости, параллельная гиперплоскости OXYZ .
Для проведения прямой hllOXY предварительно проведена ги перплоскость уровня S(Z3)II OXYZ . Строить другие проекции ги перплоскости 27 нет необходимости. В гиперплоскости 27 выбрана
плоскость |
уровня |
A(A3)IIOXYZ, |
проекции |
|
A2(A2M2N2) |
и |
||
AX(AXMXNX) |
строятся по |
точкам М и |
N, |
М GBD, |
N |
е CD |
. Гиперп |
|
лоскость 27 проведена через вершину |
А |
тетраэдра |
ABCD |
для |
эко |
|||
номии построений. Проекции h2 и hx |
прямой уровня h строятся по |
|||||||
условию принадлежности плоскости уровня А. При |
этом |
h3 II ОХ , |
||||||
h2 II OX |
,hxiOX. |
|
|
|
|
|
|
|
Построение прямой |
h, he (ABCD) |
и h II XYZ |
выполняется точно |
|||||
так же, как и в предыдущем случае. Однако теперь в плоскость A(AMN) можно выбрать любую прямую h(h2 # ОХ) и построить иро-
Рис. 3.42. Прямая уровня гиперплоскости относительно плоскости OXYZ пространства Е,
екцию Л, по принадлежности. Получаемая прямая h(huh2,h3) будет параллельна гиперплоскости OXYZ .
Если бы А, оказалась тоже параллельной оси ОХ, то это бы озна чало, что заданная гиперплоскость ABCD не является гиперплоско стью общего положения. В этом случае гиперплоскость ABCD была бы перпендикулярна гиперплоскости OYZT или, что, то же самое, была бы параллельна оси ОХ .
Очевидно, что в гиперплоскости ABCD общего положения нельзя найти и построить плоскость, параллельную какой-либо плос кости проекций.
3.б.3. Преобразование гиперплоскости общего положения в проецирующую гиперплоскость и гиперплоскость уровня
Для преобразования данной гиперплоскости общего положения в гиперплоскость проецирующую относительно какой-либо гиперпло-
А_
А-/
х- П?,П3
\ \
*2
Рис. 3.43. Преобразование гиперплоскости общего положения пространства ЕА в проецирующую гиперплоскость
86 |
8 7 |
скости проекций необходимо в данной гиперплоскости построить прямую уровня. Н а рисунке 3.43 выбрана прямая уровня А ( А , , А , , А 3 ) ,
параллельная |
плоскости |
OXY . |
Новая |
гиперплоскость |
проекций |
|||
O A ' J Z J T , |
перпендикулярна прямой h, т.е. |
± А , . В новой системе |
||||||
проекций |
гиперплоскость |
ABCD |
является проецирующей относи |
|||||
тельно плоскости ОХ ХТХ. |
|
|
|
|
|
|||
Если |
задать ось |
о2Хг |
параллельно |
вырожденной |
проекции |
|||
А5В5С505, |
то |
в новой |
системе |
проекций |
o2X2Y2Z2T2 гиперплоскость |
|||
ABCD станет гиперплоскостью уровня относительно гиперплоскости
88
ГЛАВА 4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ЛИНЕЙНЫХ ПОДПРОСТРАНСТВ
В пространстве Е3 прямая и плоскость, а также две плоскости, могут пересекаться, быть параллельными или перпендикулярными. Выполним на рассматриваемой графической модели решения пози ционных, аффинных и метрических задач для указанных пар геомет рических объектов.
4.1.Пересечение прямой и плоскости
Из аксиомы стереометрии [7]: «Если две точки прямой лежат в плоскости, то все точки прямой лежат в плоскости» следует, что прямая и плоскость могут пересекаться в точке - собственной или не собственной (бесконечно удаленной). В последнем случае прямая и плоскость являются параллельными, кроме того, исходя из формулы s = m + q-n размерности пространства пересечения (п. 1.7.2), также получаем пересечение прямой и плоскости пространства Е3 в точке, поскольку 5 = 2 + 1- 3 = 0.
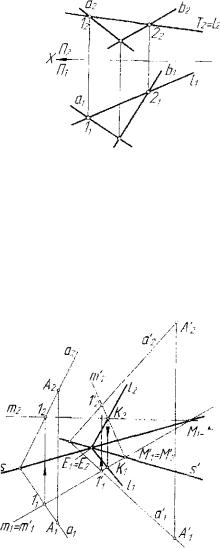
Рассмотрим алгоритм конструктивного определения точки пере сечения прямой и плоскости. Пусть на чертеже (рис. 4.1) заданы
плоскость Ф(а// в) и не принадлежащая |
ей прямая |
с(сг,с2). Требует |
ся определить точку пересечения сГ)Ф. |
Отметим, |
что существуют |
различные решения данной задачи [23]. Наиболее простое графиче ское решение ее может быть выполнено на основе применения пары конкурирующих прямых, принадлежащих одной проецирующей
плоскости. Одной прямой |
этой |
пары служит заданная |
прямая |
с, а |
||
другой - прямая |
d с Ф. В этом случае определение искомой точки |
|||||
пересечения |
с[}Ф |
сводится к определению точки пересечения |
cf]d, |
|||
поскольку |
при |
с Ф |
имеет |
место тождественное |
равенство |
|
с(]Ф - cf]d. Алгоритм решения задачи может иметь нижеследующий вид.
1.c2=d2 (прямые с и d - фронтально-конкурирующие);
2. |
d2f)a2 |
= 1 2 , d2f]e2 = 2 2 ; |
3. 12 - И , е а , , 22 —>2Х е е , ; |
||
4. |
ri, =(lj,2]) - проекция dx прямой d определена проекциями |
|
l|,2j ее точек |
1 и 2; |
|
|
|
89 |

5. |
|
|
|
|
|
|
|
|
6. |
К, |
—> /С7 e c7 |
Точка |
|
||||
К(КХ, К2) |
является |
решением |
|
|||||
задачи. |
|
|
|
|
|
|
|
|
Для полноты |
представле |
|
||||||
ния расположения прямой с и |
|
|||||||
плоскости |
|
Ф |
относительно |
|
||||
друг друга |
и |
относительно |
|
|||||
плоскостей проекций Я, и |
П2 |
|
||||||
необходимо |
рассмотреть |
оп |
|
|||||
ределение |
видимости |
прямой |
|
|||||
с при |
ее |
пересечении с плос |
|
|||||
костью Ф. Видимость опре |
|
|||||||
деляется |
относительно |
плос |
|
|||||
кости |
проекции |
с |
учетом |
на |
Рис. 4.1. Модель построения |
|||
правления |
|
проецирования. |
||||||
|
пересечения прямой и плоскости |
|||||||
|
|
|
|
|
|
|
|
|
Смысл |
сказанного |
и |
способ |
|
||||
определения видимости заключается в следующем. Предположим, что заданы: плоскость ортогонатьных проекций 77, прямая с и плос кость Ф с их точкой пересечения К (рис. 4.2). Очевидно, последняя является границей видимости прямой с относительно плоскости Ф
при проецировании на П. Возьмем на прямой с точку |
М * К |
и про |
||||||||||
ведем проецирующую |
прямую т 1 П |
такую, что |
Mem. |
11усть |
||||||||
тГ\Ф-А', |
тГ\П = |
М'. |
Тогда на прямой т |
возможны |
расположения |
|||||||
тройки |
точек |
в |
последова |
|
|
|
|
|||||
тельности, |
соответствую |
|
|
|
|
|||||||
щей |
ортогональному |
про |
|
|
|
|
||||||
ецированию |
|
на |
|
|
77: |
|
|
|
|
|||
М -> /V -> Л/' |
|
|
|
либо |
|
|
|
|
||||
N -> М |
-> М'. |
Для |
наблю |
|
|
|
|
|||||
дателя, |
расположенного |
в |
|
|
|
|
||||||
соответствии с направлени |
|
|
|
|
||||||||
ем |
проецирования |
|
перед |
|
|
|
|
|||||
тройкой |
точек, |
в |
первом |
|
|
|
|
|||||
случае будет «открытой», то |
|
|
|
|
||||||||
есть видимой, ближе распо |
Рис. 4.2. Определение видимости прямой |
|||||||||||
ложенная к нему |
точка |
М. |
||||||||||
|
|
|
|
|||||||||
при ее пересечении с плоскостью
Очевидно, что в этом случае
90
|MMJ>j/VAf|, то есть видимой является более удаленная от плоскости U т о ч к а м е с. Во втором случае имеет место ]/УМ1|>|ММ'], то есть видимой является более удаленная от плоскости П точка N е Ф. Следовательно, при ортогональном проецировании на плоскость П в первом случае получаем на П изображение [&Т'М') видимого луча [КМ) прямой с, а во втором - изображение [ЛГ'М') ее невидимого луча, расположенное справа от точки К'. Очевидно, что произволь
ное и единственное назначение точки М Ф К на прямой |
с не влияет |
|||
на результат анализа рассматриваемой видимости. |
|
|
||
На рисунке 4.1, в соответствии с изложенным, дважды определе |
||||
на видимость. |
|
|
|
|
1. Видимость относительно плоскости проекций П2 |
при помощи |
|||
фронтально-конкурирующих точек 2 € Ф и 3 е с; 22 |
= 32 , 2, Ф 3j. По |
|||
скольку у3 |
> у2, то есть точка 3 е с |
более удалена |
от плоскости П2 |
|
чем точка |
2 е Ф, то точка 3 видима при проецировании на П2 и луч |
|||
[КЗ) прямой с является видимым при этом проецировании. |
||||
2. Видимость относительно плоскости проекций Пл |
при помощи |
|||
горизонтально-конкурирующих точек |
4 е с и 5 е Ф : Лх |
= 5Ь 42 Ф 52. |
||
Гак как z5 |
> z4, то есть точка 5 € Ф |
более удалена от плоскости Я, |
||
чем точка |
4 е с, то точка 5 видима при проецировании на Пх и луч |
|||
[КЛ) прямой с является невидимым при этом проецировании. Очевидно, определение видимости прямой имеет смысл при до
пущении, что плоскость Ф представляет собой непрозрачную неогра ниченную либо ограниченную пластину бесконечно малой толщины.
|
На рисунке 4.3 на ос |
|||||
|
новании |
вышеуказанного |
||||
|
определена видимость пря |
|||||
|
мой |
с |
общего |
положения, |
||
|
пересекающей |
проецирую |
||||
|
щую |
|
плоскость |
|
Ъ LII2 в |
|
|
точке |
|
К |
при проецирова |
||
|
нии на Пу, поскольку с |
|||||
|
учетом |
указанного |
допуще- |
|||
Рис. 4.3. Модель построения |
ния, |
на плоскость |
П2 пря- |
|||
пересечения прямой общего положения |
мая с |
проецируется как ви- |
||||
с проецирующей плоскостью |
димая. |
|
|
|
||
91 |
|
|
|
|
|
|

|
На |
|
рисунке |
4.4 |
определе |
|
|
|||||||
на |
видимость |
проецирующей |
|
|
||||||||||
прямой сА-Пх, пересекающей |
|
|
||||||||||||
плоскость |
|
Ф(ААВС) |
общего |
|
|
|||||||||
положения в точке К. Для |
х- |
|
||||||||||||
анализа |
видимости |
прямой |
с |
|
||||||||||
относительно |
|
плоскости |
Ф |
|
|
|||||||||
при проецировании на П2 ис |
|
|
||||||||||||
пользуется |
пара |
фронтально- |
|
|
||||||||||
конкурирующих точек 2 е Ф |
и |
|
|
|||||||||||
Зес, |
при |
этом |
у3 |
>у2- |
|
|
Рис. 4.4. Модель построения |
|||||||
|
Рассмотрим |
|
определение |
|||||||||||
|
|
пересечения проецирующей прямой с |
||||||||||||
точки |
пересечения |
прямой |
и |
|||||||||||
плоскостью общего положения |
||||||||||||||
плоскости, заданной на графи |
||||||||||||||
|
|
|||||||||||||
ческой |
|
модели |
родством. Пусть заданы: прямая т(т1,т2) |
и плос |
||||||||||
кость Ф(я,Д, Л 2 ), |
где s - ось родства; АХ,А2 - пара соответственных в |
|||||||||||||
родстве точек, при этом |
/и<гФ |
(рис. 4.5). Требуется определить точ |
||||||||||||
ку |
пересечения |
|
т о Ф . |
Последовательность графического |
решения |
|||||||||
рассматриваемой задачи имеет нижеследующий вид. |
|
|||||||||||||
|
1. |
|
Строим прямую |
я,, соответственную прямой п2 - т2 в родст |
||||||||||
ве (s,AuA2). |
Для |
этого |
вначале |
|
|
|||||||||
назначим |
точку |
1 2 ея 2 . |
Затем |
|
|
|||||||||
построим прямую 12Л2 и опре |
|
|
||||||||||||
делим |
|
|
точку |
|
пересечения |
|
|
|||||||
12~\2A2C\s. |
|
В |
|
пересечении |
|
|
||||||||
прямой |
2, Л, |
и |
прямой |
е |
на |
|
|
|||||||
правления |
родства |
определим |
|
|
||||||||||
точку |
1], |
соответственную точ |
|
|
||||||||||
ке |
12 |
|
в |
|
родстве. |
Прямая |
|
|
||||||
я, |
= (ll,Nl) |
является искомой. |
|
|
||||||||||
|
2. |
|
Определим |
проекции |
Рис. 4.5. Модель построения |
|||||||||
искомой |
точки |
пересечения |
К: |
пересечения прямой и плоскости, |
||||||||||
|
|
|||||||||||||
ЛГ, |
= т1 |
ппи |
К, |
-> |
К2 |
ет2. |
|
заданной родством |
|
|||||
|
|
|
||||||||||||
4.2.Пересечение двух плоскостей
Исходя из формулы размерности пространства пересечения (п. 1.7.2) две плоскости в пространстве Еъ пересекаются по прямой линии, поскольку $ = 2 + 2- 3 = 1. Эта линия может быть собственной, либо несобственной. В последнем случае плоскости являются парал лельными. Рассмотрим решение задачи определения линии пересече ния двух плоскостей. Пусть на графической модели пространства за
даны |
две |
плоскости общего |
положения ЩААВС) |
и |
А(т//п) |
(рис. |
4.6). |
Требуется построить |
их линию пересечения |
Z n A . |
Алго |
ритм решения данной задачи основал на алгоритме решения преды дущей задачи (п. 4.1) и включает по существу дважды повторенное решение рассмотренной задачи. Действительно, для определения прямой линии пересечения In Д необходимы, как и для всякой пря мой, две ее точки. Каждая из них определяется как точка пересечения произвольной прямой, взятой в одной плоскости, с другой плоско стью. На основании сказанного последовательность конструктивного решения поставленной задачи может быть нижеследующей.
|
|
1. В качестве одной из |
|||||||
|
двух |
прямых, |
необходимой |
||||||
|
для |
определения |
одной |
из |
|||||
|
двух |
точек |
искомой |
линии |
|||||
|
пересечения, |
выберем |
пря |
||||||
|
мую |
т с Д. |
На |
основании |
|||||
|
алгоритма |
определения |
точ |
||||||
|
ки |
пересечения |
прямой |
и |
|||||
|
плоскости |
(п. |
4.1) выполним |
||||||
|
соответствующие |
построе |
|||||||
|
ния и определим точку перс- |
||||||||
|
сечения |
тглЪ = |
М(М1,М1). |
||||||
|
|
2. |
Выберем в плоскости |
||||||
|
Д другую |
прямую, |
напри |
||||||
Рис. 4.6. Модель построения пересечения |
мер, п и определим точку пе |
||||||||
двух плоскостей общего положения |
ресечения |
и п 1 = 7V(7V, ,N2). |
|||||||
|
|
3. |
Проведем |
|
линию |
||||
l=(M,N), которая и будет искомой линией пересечения /=Е гл Л .
92 |
93 |
|
Если одна из двух пересекаю |
|
|
|||||||
щихся |
плоскостей |
занимает |
относи |
|
|
||||
тельно |
плоскостей |
проекций |
частное |
|
|
||||
положение, решение рассматриваемой |
|
|
|||||||
задачи |
значительно |
упрощается. Рас |
|
|
|||||
смотрим этот случай. Пусть на графи |
|
|
|||||||
ческой модели заданы две плоскости |
|
|
|||||||
Pfanb) |
и |
Т 1 П2 (рис. |
4.7). |
Постро |
|
|
|||
им их линию пересечения. Поскольку |
|
|
|||||||
одна из плоскостей, а именно, плос |
|
|
|||||||
кость |
Г? является проецирующей, то |
|
|
||||||
Т2 = /2, то |
есть |
фронтальный |
след |
Т2 |
|
Рис. 4.7. Модель построения |
|||
плоскости |
Т |
есть |
одновременно |
и |
пересечения плоскости общего |
||||
фронтальная проекция искомой линии |
|
положения и проецирующей |
|||||||
|
|
||||||||
пересечения /. |
|
|
|
|
|
|
плоскости |
||
|
|
|
|
|
|
|
|||
Поэтому ее недостающая проекция |
/, |
строится по принадлежно |
|||||||
сти: /, пдг, = 1,; /, п й , |
2 2 ; 1 2 •1, ей,; |
22 -»2, е*,; (1„2,) = /, |
|||||||
Решение предыдущей задачи (рис. 4.6) может быть сведено к ре шению рассмотренной задачи, если одну из двух пересекающихся
плоское 1 ей |
|
преобразовать в |
|
||||
положение |
|
|
проецирующей |
|
|||
плоскости (рис. 3.27). Для это |
|
||||||
го потребуется |
всего |
одно |
|
||||
преобразование |
системы |
ос |
|
||||
новных |
плоскостей |
проекций, |
|
||||
например: |
X—-—»Х-- 1 . |
|
|
||||
|
|
|
|
|
|
|
Г12 |
Если на |
графической |
мо |
|
||||
дели |
обе |
|
пересекающиеся |
|
|||
плоскости |
заданы |
родством, |
|
||||
например, |
|
Ф(л, А,,А2) |
и |
|
|||
Ф\^,А\,А'2), |
|
то |
последова |
|
|||
тельность |
|
конструктивного |
|
||||
определения |
|
их линии пересе |
|
||||
чения |
может |
быть |
нижесле- |
Рис. 4.8. Модель построения |
|||
дующей (рис. 4.8). |
|
|
пересечения двух плоскостей, |
||||
|
|
|
|
|
|
|
заданных родством |
|
|
|
|
|
|
|
94 |
1. Проведем в поле "первых" проекций родственных соответст вий (s,A\,A2) и (s',A\,A'2) произвольную прямую m, =т\. Исполь зуя алгоритм построения проекций точки, принадлежащей плоскости, заданной родством (рис. 3.16), построим "вторые" проекции т2 и т'2 прямых т и от', принадлежащих соответственно плоскостям: т с Ф , /и'с Ф'. Для построения этих проекций используются вспомогатель
ные прямые |
а с Ф и а'сФ', |
проекции которых соответственны в |
|||||
родстве: |
а,, |
а2 |
- в р о д с т в е |
(s,A{,A2); |
а\, |
а\ - в р о д с т в е (s',A\,A'2). |
|
2. Определим |
точку |
К по |
ее |
проекциям |
К2= т2Г\т'2, |
||
К2 —> Кх |
е /71,, которые являются соответственными в обоих родствах |
||||||
(s,Ax,A2) |
и |
(s',A\,A'2). |
|
|
|
|
|
3.Определим искомую линию / пересечения плоскостей по ее
проекциям, |
соответственным в |
обоих родствах: |
12-(К2,Е2); |
/, = (К,, £ , ) , |
где Е]=Е2= sf]s'. |
|
|
4.3.Параллельность прямой линии и плоскости
Всоответствии с формулой (1.5) определения степени парал лельности, прямая и плоскость в пространстве Еъ вполне параллель
ны, поскольку рц =~Л = ^' ^ кУРсе стереометрии [7] известен при знак параллельности прямой и плоскости, формулированный в виде следующей теоремы: если прямая, не лежащая в данной плоско
сти, параллельна какой-нибудь прямой, лежащей в этой плоско сти, то она параллельна данной плоскости. Из признака параллель ности следует практическое указание для ее реализации на графиче ской модели пространства: построение прямой, параллельной данной плоскости, требует предварительного проведения какой-нибудь пря мой в этой плоскости. Логическая неопределенность "какая-нибудь" в признаке параллельности позволяет заданием дополнительных усло вий выделить однопараметрическое множество (пучок) прямых или единственную прямую из двухпараметрического множества прямых в плоскости, удовлетворяющих условию параллельности. В подтвер ждение сказанного рассмотрим пример. Пусть на графической модели
(рис. |
4.9) |
заданы: плоскость общего положения Ъ(а//Ь), |
точка |
||
C ( C , , C 2 ) £ l |
и проекция |
т2 прямой |
т. Требуется построить полную |
||
модель |
прямой mim^nh) |
по условиям: |
Сет, т II2 . Очевидно, |
этими |
|
|
|
|
95 |
|
|

условиями |
определена |
един |
|
||||
ственная прямая |
т простран |
|
|||||
ства. Действительно, парамет |
|
||||||
рическое |
число |
прямой |
про |
|
|||
странства Е3, на основании |
|
||||||
формулы |
(1.1), |
равно |
D ™ = 4 . |
|
|||
Определим размерность |
усло |
|
|||||
вия прохождения прямой про |
|
||||||
странства |
через |
точку. |
По |
|
|||
формуле |
(1.4) |
размерность |
Рис. 4.9. Модель построения прямой |
||||
этого условия |
<4л) вычисляет |
||||||
линии, параллельной плоскости |
|||||||
|
|
|
|
|
|
||
ся следующим образом: |
|
|
|
||||
|
|
|
|
|
( 2 - 3 - 1 И 1 + 1) •(3 + 0) = 2. |
||
Признак (условие) параллельности прямой и плоскости про |
|||||||
странства |
Е3 |
имеет размерность, вычисляемую по формуле (1.6): |
|||||
Q,, = 1 • 1 -(3-1 -2 + 1 • I ) - 1. Условие задания одной проекции т2 ис- |
|||||||
„ |
|
|
|
|
|
1,0 |
|
комой прямой т имеет символическое представление: е2>0, и его раз мерность может быть вычислена по формуле (1.4) следующим обра зом:
Таким образом, сумма размерностей указанных условий задачи равна Qo6{^) + Qii+Qo6{exo) = Dn = 4, ч т о говорит о корректности поставленной задачи и единственности ее решения. На основании признака рассматриваемой параллельности и проведенного анализа условия задачи выполним ее конструктивное решение в следующей
последовательности: |
|
1. т2 п а2 = 12, |
nb2 =22; |
2.12 - >1, еа, , 22 - >2, е/>,;
3.0 „ 2 | ) = /1;
4.щП\х, С, еот,.
Построенная прямая т^пц,)?^) является искомой. Вспомогатель ная прямая Щх,12 -щ) является, в соответствии с отмеченной выше логической неопределенностью "какая-нибудь", прямой пучка парал-
96
лельных прямых в плоскости X, выделенного из двухпараметрического множества прямых этой плоскости условием задания проекции /2 = т2 прямой /. Это условие, как было показано выше, имеет раз мерность Qo6(e2^0) = }.
4.4.Параллельность двух плоскостей
Всоответствии с формулой (1.5) степени параллельности две
плоскости |
в |
пространстве |
Е3 |
вполне |
параллельны, поскольку |
1 + 1 |
= 1. |
В стереометрии |
[7] |
известен |
признак параллельности |
Р/1 |
|
|
|
|
|
двух плоскостей, выраженный следующей теоремой: если две пере
секающиеся прямые одной плоскости соответственно параллель ны двум прямым другой плоскости, то эти плоскости параллель ны. Из признака параллельности следует практическая рекомендация по определению плоскости, параллельной данной: необходимо про вести две пересекающиеся прямые в данной плоскости, а искомая плоскость определится парой пересекающихся прямых, соответствен но параллельных проведенным пересекающимся прямым. Рассмотрим
|
|
|
|
решение задачи. Пусть |
||||
|
|
|
|
на |
графической |
моде |
||
|
|
|
|
ли |
заданы |
плоскость |
||
|
|
|
|
Ъ(А, а) |
и точка |
М <£ £ |
||
|
|
|
|
(рис. |
4.10). Требуется |
|||
|
|
|
|
построить плоскость Л |
||||
|
|
|
|
по |
следующим |
усло |
||
|
|
|
|
виям: |
Me А, |
А//Е. |
||
|
|
|
|
Этими |
условиями оп |
|||
|
|
|
|
ределяется |
единствен- |
|||
Рис. 4.10. Модель построения параллельных |
н а я |
плоскость. |
Дейст- |
|||||
|
|
плоскостей |
|
вительно. |
Параметри |
|||
ческое |
число плоскости пространства Е3, |
согласно формуле (1.1), |
||||||
равно |
D™ - (3 - 2) • (2 +1) = 3. Условие прохождения плоскости через |
|||||||
точку |
имеет |
символическое |
представление |
е ^ о » |
и |
е г о размерность |
||
определяется |
в соответствии |
с формулой (1.4) следующим образом: |
||||||
/\ , 2.1ЛК |
( 2 - 3 - 2 ) - ( 2 + 1) |
(3 + 2 + 0) = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
97 |
|
|
|
|
|
Учитывая, что две плоскости в пространстве Е3 вполне парал лельны, поскольку их степень параллельности по формуле (1.5) равна
Pn = ^ Г ~ = ^' 0 |
П Ре Де л и м по формуле (1.6) размерность этой парал |
лельности: Qlt |
= 1 - 2 - ( 3 - 2 - 2 + 1-2) = 2. Таким образом, получаем |
равенство параметрического числа плоскости пространства и суммы размерностей условий задачи:
Следовательно, |
условия |
рассматриваемой задачи |
корректны |
и |
||
она имеет единственное решение. |
|
|
|
|||
Алгоритм решения задачи в соответствии с признаком парал |
||||||
лельности может быть нижеследующим |
|
|
||||
1. |
В плоскости проекций 772 |
проведем линию А2 |
е /2; |
|
||
2. |
/7 |
ел |
а2 |
= |
12 |
'•> |
3.12 —» 1, Ё Й , ;
4.( 1 „ 4 ) = V.
5. т2 II а2, М2 е от7. тх II ах, Мх е гпх;
6.п2 II /2, М2 е и2, л, /7 /[, Л/, е /г,.
Искомая плоскость А определена двумя пересекающимися пря мыми т(тх,т2) и «(«,, л 2 ), при этом mil и, п/11.
Решение данной задачи можно представить как дважды повто ренное решение предыдущей задачи (п. 4.3). Действительно, из при знака параллельности двух плоскостей следует, что если каждая из двух пересекающихся прямых параллельна плоскости, то плоскость этих прямых параллельна этой плоскости. Поэтому вышеприведен ный алгоритм можно представить в следующем кратком виде:
1. тИИ, М ет;
2.nllzZ, М е п.
4.5.Перпендикулярность прямой и плоскости
Прямая и плоскость в пространстве £3 вполне перпендикулярны, так как согласно формуле (1.8) степень их перпендикулярности равна
0 + 1 |
1 |
г, |
рх = —— = 1. В стереометрии известен признак перпендикулярности прямой и плоскости [7], выраженный следующей теоремой: если
прямая перпендикулярна двум пересекающимся прямым, лежа-
1 ц и м в плоскости, то она перпендикулярна этой плоскости. В со ответствии с признаком, для построения прямой, перпендикулярной данной плоскости, необходимо в этой плоскости предварительно про вести две пересекающиеся прямые, а затем добиваться перпендику лярности искомой прямой каждой из проведенных пересекающихся прямых. Таким образом, решение задачи о перпендикулярности пря мой и плоскости основано на решении задачи о перпендикулярности двух прямых (пересекающихся или скрещивающихся). Рассмотрение перпендикулярности двух прямых на графической модели основыва ется на теореме о проекции прямого утла: если одна сторона прямо
го угла параллельна плоскости проекций, а другая ей не перпен дикулярна, то на эту плоскость проекций прямой угол проециру ется без искажения. Рассмотрим доказательство этой теоремы. 11усть
ZABC = 90°, стороны прямого |
угла удовлетворяют условиям: |
сторо |
||||||||||||
на А В параллельна плоскости |
проекций |
П; |
сторона |
ВС |
не |
перпен |
||||||||
дикулярна и не параллельна плоскости проекций |
П (рис. |
4.11). До |
||||||||||||
|
|
кажем, |
что |
|
/.А' В' С=90°. |
|
По |
|||||||
|
|
скольку |
АВ I! П и |
А' В' |
есть |
ор |
||||||||
|
|
тогональная |
|
проекция |
стороны |
|||||||||
|
|
АВ, |
то |
АВИ А'В'. |
|
Прямая |
|
А В |
||||||
|
|
перпендикулярна |
|
|
плоскости |
|||||||||
|
|
Ф(ВСГ\ВВ'), |
где |
В В' |
- |
|
проеци |
|||||||
|
|
рующая |
прямая |
(ВВ'1 |
Л). |
Дей |
||||||||
|
|
ствительно. |
|
АВ ± ВС |
|
но |
усло |
|||||||
|
|
вию |
теоремы |
и |
ABLBB', |
так |
||||||||
|
|
как |
ВВЧП |
и |
АВ//П. |
|
На |
осно |
||||||
Рис. 4.11. Интерпретация теоремы о |
вании признака перпендикуляр |
|||||||||||||
ности прямой и плоскости сле |
||||||||||||||
проекции прямого угла |
|
|||||||||||||
|
дует, что АВ |
± Ф. Из известно |
||||||||||||
|
|
|||||||||||||
го в стереометрии определения прямой, перпендикулярной плоскости [7]: прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости - из этого определения следует, что перпендикулярная прямая перпенди кулярна любой прямой в этой плоскости. Поэтому из перпендикуляр ности АВ _1_ Ф следует А В X В'С, поскольку Д ' С ' с Ф как линия пе ресечения ФпП = В'С. А поскольку АВИА'В', то А'В'1В'С, то есть Z.A' В'С— 90°. Если ВС//Л, то утверждение теоремы очевидно.
98 |
99 |
