
1671
.pdfточке алгебраической кривой существует / соприкасающихся плос костей, но одной для каждой ветви, которые являются проецирующи ми плоскостями для центра проецирования, совпадающего с / - кратной точкой. В итоге центральная проекция исходной алгебраиче ской кривой с центром проецирования в ее / -кратной точке пред ставляет собой на плоскости проекций множество линий, состоящее из криволинейной составляющей и г" прямых пересечения / соприка сающихся плоскостей с плоскостью проекций. Поэтому порядок этой криволинейной составляющей равен п ~ i.
3. Жанр (род) алгебраической кривой и ее проекции равны.
Это свойство следует из понятия жанра кривой (число, представ ляющее собой разность между наибольшим числом двойных точек, которое может иметь кривая данною порядка, и их фактическим чис лом) и взаимно однозначного соответствия, устанавливаемого при линейном проецировании между множествами точек кривой и мно жеством точек се проекций. На основании этого свойства жанр кри вой линии может быть определен по ее проекции, и проекцией рацио нальной кривой, у которой наибольшее число двойных точек равно их фактическому числу, является рациональная кривая.
4. Если каждая проецирующая прямая пересекает алгебраиче скую кривую порядка п в /' точках, то проекция этой кривой имеет порядок n:i.
Из свойства 1 следует, что порядок конической поверхности, проходящей через кривую гс-го порядка, равен п. В рассматриваемом случае коническая поверхность порядка п с вершиной в центре про ецирования распадается на / совпавших конических поверхностей, каждая из которых имеет порядок п: i. Следовательно, при указанных условиях порядок проекции исходной кривой порядка п будет равен
п: i.
Приведенные свойства 1-4 имеют место в общем случае также для параллельного и ортогонального проецирований.
ГЛАВА 6. ОБРАЗОВАНИЕ ПОВЕРХНОСТЕЙ
В данной главе будут рассмотрены вопросы образования кривых поверхностей, т.е. поверхностей, не являющихся объединением ко нечного числа плоских фигур, к которым относятся всевозможные пирамиды, призмы, призматоиды и другие многогранники. По самому общему определению поверхность есть непрерывное двумерное мно жество точек. Это видно хотя бы из аналитического описания поверх ности. Если в пространстве выбрать систему координат OXTZ, то по верхность может быть представлена в виде следующих уравнений:
- явного z - f(x, у);
-неявного F(x, у, z) = О;
-параметрического х - х(и, v), у = у(и, v ) , z - z(u, v ) .
Исходя из этого, поверхность можно рассматривать как одномер ное непрерывное множество линий, неважно, плоских или простран ственных. Следует только иметь в виду, что одномерное непрерывное множество плоских линий, расположенное в одной плоскости, по верхностью не является. Такое множество линий называется пучком. Е1о между поверхностью и пучком есть непосредственная связь: если параметру пучка придать конструктивный смысл (например, считать его равным расстоянию кривой линии от плоскости пучка), то пучок можно "раздуть" в поверхность. Простейшим примером такой связи можно считать связь между семейством (пучком) концентрических
окружностей х2 + у2 |
= г2 в плоскости OXY и конусом с осью OZ, ес |
ли параметр пучка г |
связать с аппликатой z окружности по правилу: |
г = z или z = аг + Ъ . |
|
Следует иметь в виду, что классификации поверхностей, исчер пывающей все их виды, не существует. Существуют различные част ные классификации классификации по какому-либо одному при знаку. Например, широко распространена классификация но виду ли ний, образующих поверхность. Линии, образующие поверхность, на зывают образующими. В зависимости от вида образующих могут быть получены следующие поверхности:
-линейчатые (образующие - прямые линии);
-циклические (образующие окружности);
-эллиптические, параболические, гиперболические (образующи ми являются соответственно эллипсы, параболы, гиперболы);
180 |
181 |
|

- общего вида, не имеющие специального названия (образующи ми являются плоские или пространственные кривые, в частности ал гебраические, порядок которых больше двух).
Поверхность можно представить как траекторию движения обра зующей в пространстве по определенному закону. Классификация по верхностей по закону движения образующей может быть следующей:
-поверхности вращения (образующая вращается вокруг прямо линейной оси);
-поверхности переноса (образующая совершает плоскопарал- лелы-юе движение);
-поверхности конгруэнтных линий (образующая совершает движение общего вида).
Эти и всякие другие классификации объединяет одна общая зави симость: если размерность множества линий в пространстве равна к, то размерность множества этих же линий на поверхности (т.е. обра зующих) равна единице. Отсюда вытекает нижеследующее правило образования поверхностей.
Для того чтобы образовать поверхность из заданного в простран стве множества линий, необходимо:
1) наложить на это множество какие-либо связи, суммарная раз мерность которых равна к-);
2) обеспечить условие совместимости (совместности) этих свя
зей.
Таким образом, для каждой линии, которую предполагается ис пользовать в качестве образующей, необходимо иметь перечень все возможных связей с рассчитанными заранее значениями размерно стей этих связей.
Следуя сформулированному правилу, рассмотрим образование некоторых поверхностей.
6.1.Образование линейчатых поверхностей
Как было описано выше, размерность множества прямых в про странстве Е3 равна четырем. Чтобы получить одномерное множество прямых, следует связать три параметра из четырех, т.е. выбрать усло вия, суммарная размерность которых будет равна трем.
Для этого рассмотрим все условия, которые могут быть наложе ны на прямую, и определим их размерность (табл. 6.1).
182
|
Прохождение через данную точку |
~> |
Пересечение данной прямой |
3.Пересечение данной кривой в одной точке
4.Пересечение данной кривой в двух точках
5.Параллельность данной прямой
6.Перпендикулярность данной прямой
7.Параллельность данной плоскости
8.Перпендикулярность данной плоско сти
9.Касание данной кривой
10.Касание данной поверхности Перпендикулярность данной поверх ности
12.j Параллельность данной поверхности
13. ! Пересечение двух линий в соответст- ! венных точках
Табл. 6, Размерность
Значение |
Обозначение |
|
|
условия |
|
2 |
. _ ^ |
|
А |
||
1 |
||
1 |
|
|
2 |
А |
|
2 |
В. |
|
1 |
|
|
1 |
|
|
2 |
|
|
3 |
С, |
|
1 |
|
|
2 |
С} |
|
2 |
с, |
|
|
С\ |
Следует иметь в виду, что некоторые условия, сформулирован ные по-разному, могут означать одно и то же. Например, если взять сферу, то условие №11 будет эквивалентно условию № 1 , так как все прямые перпендикулярные сфере, проходят через ее центр. Если взять цилиндр вращения, то условие №11 будет эквивалентно двум одно временно наложенным условиям №2 и №6. В этом случае использует ся термин - произведение условий №2 и №6.
Что касается совместности двух и более условий (произведение условий), то, например, условия №10 и №11 несовместны для одной и той же поверхности. И так далее.
Рассмотрим некоторые поверхности.
1. Поверхность, представляющая собой множество прямых, пе ресекающих три прямые а, Ь, с общего положения. Эта поверхность хорошо известна и описана во многих учебтжах по начертательной
183
геометрии. Она называется однополостным гиперболоидом. Порядок
ееравен двум. Поверхность получена трехкратным условием №2.
2.Обобщением однополостного гиперболоида будет поверх ность, п о р ч е н н а я при помощи трехкратного условия № 3 . Если н про
странстве задать три кривые а, Ь, с порядков, соответственно
,к-,, к,, то образованная поверхность будет иметь порядок 2кхк2къ.
3.Использование условия №7 в сочетании с двукратными усло виями №2 или №3 порождает поверхности с плоскостью параллелиз ма: с №2 и №2 - косую плоскость; с №2 и №3 - коноид; с №3 и №3 - цилиндроид.
4.Одновременное наложение условий №1 и №3 приведет к об разованию конических поверхностей, порядок которых будет равен
порядку кривой направляющей поверхности.
Одновременное наложение условий №5 и №3 приводит к образо ванию цилиндрических поверхностей.
Использование условий №3 и №8 дает образование прямых ци линдрических поверхностей.
5.Если в условии №9 будет выбрана пространственная кривая линия, то образуется торсовая поверхность с ребром возврата.
6.Сочетание условий №2, №3, №6, в которых используется одна
ита же прямая, а кривой линией является винтовая линия, осью кото рой является эта же прямая, приводит к образованию прямого закры того геликоида.
Заменив в предыдущем предложении условие №2 на условие №10, поверхностью которого является цилиндр с осью - той же пря мой, получим прямой открытый геликоид.
Очевидно, что условие №6 может быть заменено условием скре щивания с прямой под данным углом. С помощью такого условия мо гут быть получены косые геликоиды.
Кроме того, косые геликоиды могут быть образованы сочетанием условия №12 с двукратным условием № 3 . Поверхностью в условии №12 будет прямой круговой конус, а пространственными кривыми - винтовые линии с общей осью - осью конуса.
Рассмотрим все это более подробно.
Условие прохождения прямой через заданную точку в символах исчислительной геометрии можно представить как е\'^.
Условие пересечения прямой с заданной прямой или кривой в символах исчислительной геометрии можно представить как е1^ или
w-ejj , где т -~ порядок алгебраической кривой.
Известна формула размерности инцидентности [5]:
(2п-т)(т + \) £^
2;=о '
Всоответствии с этой формулой условие el'°0 имеет размерность
(2-3 ! ) ( ] . 1 )
2 |
(3 + 0) = 2, а размерность условия e3f равна |
|
|
(2-3-1X1 + 1) - ( 3 + 1) = 1. |
|
6.1.1.Линейчатые поверхности общего вида
Для задания одной из линейчатых поверхностей выберем условия <?!'д и
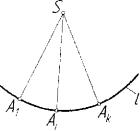
m-el'j. Эта поверхность является кони ческой и ее в трехмерном пространстве можно представить как на рисунке 6.1.
Если т принять равным единице, то получим частный случай конической поверхности - плоскость. Используя методы исчислительной геометрии, можно определить порядок конической поверхности. Так, если направляющая /
имеет порядок т, то порядок конической поверхности будет равен
4:2 •• 4;? • 4:,° = 4:2 • - • (4:2 + 4?) =«• (4:2)2+«• 4:2 •е\1 = т'е\,
+ т - 0 - те\1]. При этом квадрат условия е3"" раскладывается на
шквадрат условия е\\ рг
сумму условий ejg +4д» квадрат условия е3'о равен е ^ , а произведе ние условий е3'ц -е2'° равно нулю [4]. т при символьном условии е\'% определяет порядок конической поверхности. На чертеже Монжа ко ническая поверхность может быть задана с помощью вершины 5 и направляющей /. Задавая горизонтальную и фронтальную проекции
1 8 4 |
185 |
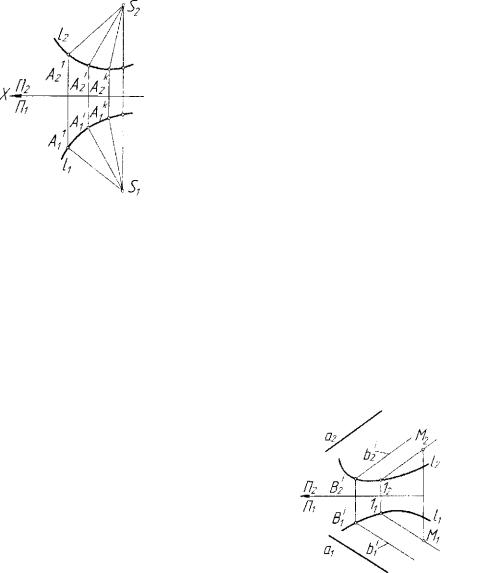
вершины и направляющей, получим чер |
|
||||
теж конической поверхности (рис. 6.2). |
|
||||
Все остальные |
линейчатые поверхно |
|
|||
сти можно представить в символах исчис- |
|
||||
лительной геометрии как те\\ • nel'°x • ре\,{\. |
|
||||
Это означает, что задана линейчатая по |
|
||||
верхность тремя |
направляющими линия |
|
|||
ми, из которых первая кривая имеет поря |
|
||||
док т, |
вторая - |
и, |
а третья - |
порядок р. |
|
Определим порядок такой линейчатой по |
|
||||
верхности. |
Он |
будет |
равен: |
|
|
melj • nebj • ре\'°х • е'3'° = 2тпр . Эта поверх |
|
||||
ность называется цилиндром. Если т,п,р |
Рис. 6.2. Чертеж |
||||
|
|||||
равны |
единице, |
то |
порядок |
линейчатой |
конической поверхности |
|
|||||
поверхности будет равен двум. Получим однополостный гиперболо ид. На чертеже эту поверхность можно задать тройкой попарно скре щивающихся прямых (рис. 6.3). Допустим, что заданы попарно скре щивающиеся прямые а{ах,а2)\ b(bx,b2) и с ( с | , с 2 ) , которые задают однопараметрическое множество образующих - прямых линий. Если
на одной |
из |
прямых, например с(сх,с2), |
выбрать |
точку N(N\,N2), то |
|||||||||
можно определить одну из образую |
|
|
|
|
|||||||||
щих, которая будет пересекать пря |
|
|
|
|
|||||||||
мую а(ах,а2) |
в |
|
точке |
M(Ml,M2), а |
|
|
|
|
|||||
прямую |
|
b(bx,b2) |
- |
в |
точке |
К(КХ,К2). |
|
|
|
|
|||
Так как на прямой с(сх,с2) существует |
|
|
|
|
|||||||||
однопараметрическое |
множество то |
О ? / , |
|
|
|||||||||
чек, то |
|
получаем |
однопараметриче- |
|
// |
! |
|
||||||
|
|
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ределетжя |
образующей, |
проходящей |
/7; |
|
|
|
|||||||
|
|
|
|
||||||||||
через |
точку |
N(NX,N2). |
представим |
|
|
--г |
|||||||
вначале плоскость с помощью прямой |
|
|
|
|
|||||||||
а(ах,а2) |
|
и |
точки |
N(NX,N2), |
затем |
|
|
|
|
||||
|
|
м |
|
|
|||||||||
найдем пересечение прямой b(bx,b2) с |
|
|
|
||||||||||
|
|
|
|
||||||||||
этой плоскостью. Решая позиционную |
|
Рис. 6.3. Чертеж |
|||||||||||
задачу, |
найдем |
точку |
К{КХ,К2) пере |
|
|||||||||
однонолостного гиперболоида |
|||||||||||||
сечения |
прямой |
b(bx,b2) |
с выбранной |
||||||||||
|
|
|
|
||||||||||
плоскостью. Тогда прямая KN(K1Nl,K7N2), пересекающая прямую а(ах,а2) в точке М(МиМ2), будет единственной образующей, про ходящей через точку N(NltN2) прямой с(с\,с2).
Рассмотрим возможные случаи линейчатых поверхностей с тремя направляющими:
1.Три направляющие - кривые линии;
2.Две направляющие - кривые линии и одна - прямая. Порядок
такой линейчатой поверхности, как было показано выше, равен (2т • п), где т и п порядки криволинейных направляющих.
3.Одна направляющая - кривая линия и две направляющие - взаимно скрещивающиеся прямые. Порядок такой линейчатой по верхности равен 2т, где т порядок направляющей кривой линии
4.Все три направляющие - попарно скрещивающиеся прямые
линии.
Рассмотрим линейчатые поверхности, которые образуются, если
вкачестве геометрических условий выбрать условия инцидентности и I гараллельности.
Представим, что заданы условия инцидентности: |
т-e\_\• |
Первое условие выражает пересечение прямых пространства |
Е3 с |
произвольно заданной прямой и его размерность равна единице. Вто рое условие выражает пересечение прямых пространства Е3 с произ вольно заданной кривой m - го порядка и его размерность также равна единице. Введем условия параллельности: параллельность прямой за
данной прямой. На основании |
формулы |
степени |
параллельности |
|||||||
|
р,,-- |
, |
где |
т |
- |
размерность линей - |
||||
|
ного объекта, степень которого опреде |
|||||||||
|
ляется, к - размерность бесконечно |
|||||||||
|
удаленного линейного |
объекта |
пересе |
|||||||
|
чения заданного и выбранного линей |
|||||||||
X- |
ных объектов. Для нашего случая |
т = 1 |
||||||||
|
— размерность |
прямой, а |
А = 0 |
- раз |
||||||
|
мерность |
бесконечно |
удаленного объ |
|||||||
|
екта |
пересечения |
двух |
параллельных |
||||||
|
прямых, |
т.е. |
точки. |
Отсюда |
следует, |
|||||
что степень параллельности будет рав
Рис. 6.4. Чертеж |
на единице. А размерность этого усло |
|
цилиндрической поверхности |
||
вия, исходя из формулы размерности |
||
|
||
|
187 |
186

параллельности Q/f = p/f |
• m(n-m-q + p^-m), равна двум, поскольку |
Qll =1 - 1(3 - 1 - 1 + + 1-1) = 2. |
|
Выбирая из условий |
инцидентности условие т-е™, а из условий |
параллельности - данное рассмотренное условие, получим, что сум марная размерность равна трем, и из четырехпараметрического мно гообразия прямых выделяется тогда одноиараметрическое многообра зие прямых, которое определяет цилиндрическую поверхность (рис. 6.4). На чертеже эта поверхность может быть задана своим гео
метрическим |
определителем, |
т.е. |
направляющей кривой /(/15/2) и |
|
прямой линией а(щ,а2), которой |
будут параллельны |
образующие. |
||
Выбирая на |
направляющей |
Щ\,12) |
некоторую точку |
В'(В\,В2), мож |
но построить образующую bl(b\,b2) этой цилиндрической поверхно сти. Сформулируем условие принадлежности точки заданной поверх ности. Точка принадлежит заданной поверхности, если она принад лежит некоторой линии этой поверхности. Зададим, например, гори зонтальную проекцию М, некоторой точки М. Необходимо постро ить ее фронтальную проекцию при условии, что точка принадлежит поверхности. Через горизонтальную проекцию М, проводим обра зующую цилиндрической поверхности, определяем проекцию 1, точ ки 1 ее пересечения с направляющей /. Строим фронтальную проек цию 12 точки 1 при условии, что она принадлежит направляющей /. Через точку 12 проводим фронтальную проекцию образующей. На фронтальной проекции образующей строим фронтальную проекцию М2 точки М.
Введем новое условие параллельности: параллельность прямой некоторой заданной плоскости. Степень параллельности прямой к и
плоскости также будет равна единице: Рц = —— = h так как прямая,
параллельная плоскости, имеет с ней общую бесконечно-удаленную точку. Размерность этого условия равна единице: 0// = 1-1(3-2-1 + + 1-1) = 1. Исходя из условий инцидентности и параллельности пря мой заданной плоскости, можно образовать три вида линейчатых по верхностей, суммарная размерность условий которых будет равна трем.
188
6.1.2.Поверхности Катачана
1.Цилиндроид - линейчатая1 поверхность, у которой направ ляющими являются две линии, не лежащие в одной плоскости, на пример, кривые т-го порядка а(аиа2) и n-го порядка b(bx,b2) и плоскость параллелизма 27(27,), которой будут параллельны все обра
зующие - прямые линии (рис. 6.5). Выберем на одной из проекций на правляющей кривой а(ах,а2)точку С[, и через эту точку проведем горизон тальную проекцию т\ образующей т'.
|
Строим фронтальную проекцию С2 |
||
|
выбранной точки |
С, а затем фронталь |
|
|
ную проекцию 12 |
точки 1 пересечения |
|
|
образующей т |
с направляющей Ь. |
|
Of |
Через точки С'2 и 12 проводим фрон- |
||
Рис. 6.5. Чертеж |
тальную проекцию одной из образую- |
||
поверхности Каталана |
щ и х и' |
, ^ ) . |
|
2.Коноид - линейчатая поверхность, у которой направляющими
линиями являются кривая а(ах,а2) порядка т , прямая линия b{bx,b2) и плоскость параллелизма Л(А2), которой будут параллельны все об разующие - прямые линии (рис. 6.6). Построим одну из образующих
данной поверхности. Для этого выберем на проекции |
а2 направляю |
|||
щей а точку N\ по произволу и построим ее горизонтальную проек |
||||
|
цию TV,. Затем построим фронталь |
|||
|
ную проекцию т\ образующей па |
|||
|
раллельно фронтальной проекции Л2 |
|||
|
плоскости |
А. Определим |
проекцию |
|
|
12 точки J |
пересечения образующей |
||
|
с направляющей Ь. Построим гори |
|||
|
зонтальную проекцию 1] точки 1. |
|||
|
Через точки N\ и 1, проведем гори- |
|||
Рис. 6.6. Чертеж коноида |
зонтальную |
проекцию |
т[ |
образую- |
|
||||
|
189 |
|
|
|
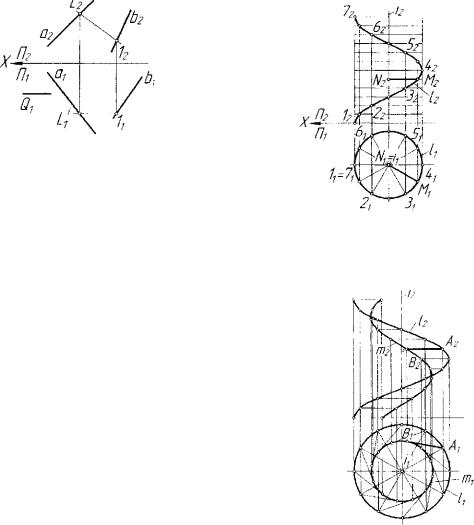
щей т'. Порядок данной поверхности равен 2т.
3 Однополостный гиперболоид - линейчатая поверхность, у ко торой направляющими являются две взаимно скрещивающиеся пря
мые а{аиа2), Ь(Ьг,Ь2) и плоскость па- |
• ' |
||||||
раллелизма Q{Q\), которой будут па |
|
||||||
раллельны все образующие |
(Рис- |
|
|||||
6.7). Построим одну из образующих |
|
||||||
этой поверхности. Для этого выберем |
|
||||||
на одной из направляющих, например, |
|
||||||
на а(ах,а2), точку |
П . |
Задаем |
Е\ |
и |
|
||
строим |
фронтальную |
проекцию |
L\ |
|
|||
точки L . Через 1\ |
проводим горизон |
Рис. 6.7. Чертеж |
|||||
однополостного гиперболоида |
|||||||
тальную |
проекцию |
образующей |
па |
||||
|
|||||||
раллельно плоскости Q(Qi). Находим точку 1, пересечения этой гори зонтальной проекции с /?,. Строим фронтальную проекцию 12 точки
1. Через гочкч L'2 и 12 проводим фронтальную проекцию образую щей. Рассмотренные три вида линейчатых поверхностей в учебной литературе называются поверхностями Каталана.
6.1.3.Геликоиды
Рассмотрим образование и задание линейчатых поверхностей, которые определяются условиями инцидентности, параллельности и перпендикулярности.
Напомним понятие степени перпендикулярности р±. Под степе-
нью перпендикулярности будем понимать отношение р± = |
|
, где |
|
Я
г - размерность объекта, инцидентного бесконечно-удаленному объ екту, полярному к т - мерному объекту, т - размерность меньшего по размерности из рассматриваемых перпендикулярных объектов.
Размерность условия перпендикулярности определяется по из вестной форму ле QL - р± • q(m ~ <? + /?х ' <?) • Степень перпендикуляр ности прямолинейной образующей к заданной прямой равна единице,
1 + 0 поскольку р± = —— = 1 .
Определим размерность условия перпендикулярности прямоли нейной образующей к заданной прямой. Она равна Q± = \-1(1-1 + + Ы ) = 1.
|
Рассмотрим конструирование линей |
|||
|
чатых поверхностей, определяемых усло |
|||
|
виями инцидентности, параллельности и |
|||
|
перпендикулярности. |
Линейчатые |
по |
|
|
верхности, которые определяются этими |
|||
|
условиями, называются геликоидами. |
|
||
|
1. Прямой закрытый геликоид обра |
|||
|
зуется сложным движением прямой ли |
|||
|
нии - образующей, которая перпендику |
|||
|
лярно пересекает ось и пересекает винто |
|||
|
вую линию (рис. 6.8). Определитель пря |
|||
|
мого закрытого геликоида состоит из оси |
|||
|
i(it,i2), винтовой линии |
/(/,,/2) и геомет |
||
Рис. 6.8. Чертеж прямого |
рических условий: образующая пересека |
|||
ет ось /(/|,/2), винтовую линию /(/,./-.) и |
||||
геликоида |
||||
перпендикулярна оси |
i(il,i2'). Каждое |
из |
||
|
||||
этих условий имеет размерность, равную единице. Суммарная раз мерность геометрических условий равна трем. Остается свободным
|
один параметр, который и определит |
||||
|
однопараметрическое семейство обра |
||||
|
зующих или прямой закрытый гели |
||||
|
коид. Построим одну из его образую |
||||
|
щих. Укажем на винтовой линии про |
||||
|
извольную точку |
М ( М ] , М 2 ) . Прове |
|||
|
дем |
фронтальную проекцию обра |
|||
X Лх |
зующей, которая |
перпендикулярна к |
|||
оси |
г(ц,г2) и пересекает |
последнюю в |
|||
|
точке N(NX,N2). Затем через точки 7У, |
||||
|
и М, проведем горизонтальную про |
||||
|
екцию этой образующей. |
|
|||
|
|
2. Прямой |
открытый геликоид |
||
|
задается осью, двумя направляющими |
||||
Рис. 6.9. Чертеж прямого |
винтовыми |
линиями |
/(/[, / 2 ) , |
||
|
|
|
лч |
|
|
открытого геликоида |
т(тv |
.,т2) lJ |
(рисr . |
6.9)' . |
Размерностьг |
190 |
191 |
|
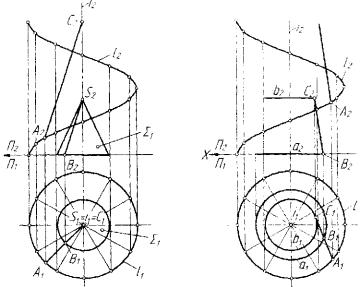
суммарного условия равна трем, так как размерности пересечения прямолинейной образующей с / и т равны каждая единице, а раз мерность условия перпендикулярности образующей к оси / также равно единице. Построим одну из образующих геликоида. Пусть на направляющей /(/15/2) выбрана точка А(А},А2). Через фронтальную проекцию А2 точки А проводим фронтальную проекцию образую щей. Находим точку В2 пересечения ее с проекцией щ направляю
щей т. |
Строим горизонтальную проекцию Вх точки В. Через |
точки |
Ах и Вх |
проводим горизонтальную проекцию образующей. Как |
видно |
из чертежа, образующая является перпендикулярной к оси / и с ней скрещивается. Это говорит о том, что геликоид прямой и открытый.
3. Косой или наклонный закрытый геликоид задается осью /'(/,,;2), направляющей винтовой линией /(/,,/2) и конической поверх ностью 27(2,, 2 2 ) , которой будут параллельны образующие (рис. 6.10). Суммарная размерность заданных условий будет равна трем. Размерности условий пересечения образующей с осью / и с направляющей / каждая будет равна единице. Размерность условия
X-
Рис. 6.10. Чертеж наклонного |
Рис. 6.11. Чертеж косого |
закрытого геликоида |
открытого геликоида |
параллельности образующих конической поверхности и геликоида также будет равна единице. Построим одну из образующих геликои да. Для этого выберем на направляющей /(/,,/2) по произволу точку А(А1,А2). Соединим горизонтальную проекцию Ах точки А с вырож денной проекцией i, оси i. Построим фронтальную проекцию B2S2 образующей конической проекции, горизонтальная проекция B]S] ко торой совпадает с проекцией ДС, образующей геликоида. Затем по строим фронтальную проекцию А2С2 образующей геликоида парал лельно фронтальной проекции B2S2 образующей конической поверх ности.
4. Косой открытый геликоид задается направляющей винтовой линией /(/],/2) и однополостным гиперболоидом, образующим кото рого параллельны соответствующие образующие геликоида (рис. 6.11). Однополостный гиперболоид задается направляющей ок ружностью а(аг,а2) и горловой окружностью Ь(Ьг,Ь2), которой каса ются прямолинейные образующие гиперболоида. Построим одну из образующих геликоида. Выберем на направляющей /(/];/2) точку А(А{,А2). Через проекцию Ах точки А проведем горизонтальную проекцию образующей, которая касательна к горловой линии b(b{,b2) и пересекает1 направляющую окружность а(ах,а2) гиперболоида в точке В(В{,В2). Затем построим проекцию В2С2 образующей гипер болоида. Через точку А2 проведем линию параллельно В2С2. Эта ли ния и проекция А1С1 представляет собой две проекции образующей рассматриваемого геликоида.
6.2. Образование поверхностей, несущих семейство кривых второго порядка
Частными видами поверхностей, несущих семейство кривых вто рого порядка, являются циклические поверхности. Циклическая по верхность несет семейство окружностей постоянного или переменно го радиуса, центры которых располагаются на плоской или простран ственной кривой. Если при этом плоскости окружностей перпендику лярны линии центров, го поверхность называется трубчатой.
Образующими поверхности будем считать следующие кривые второго порядка:
192 |
193 |
|
- окружности, размерность множества которых в пространстве
£, равна 6;
-параболы, размерность множества которых в пространстве £,
равна 7; |
|
|
|
|
|
|
|
- эллипсы и гиперболы, размерность множества каждого из кото |
|||||
рых в пространстве Еъ |
равна 8. |
|
|
|
||
|
Условиями, комбинации которых образуют поверхность, будут |
|||||
следующие (табл. 6.2). |
|
|
|
|
|
|
|
|
|
|
|
|
Табл. 6.2. |
|
|
|
|
|
Размер |
Обозна |
|
|
|
|
|
|
|
№ |
Условие на образующую |
|
ность |
чение |
||
|
|
|
|
|
условия |
условия |
|
|
|
|
|
||
1. |
Пересечение с прямой или кривой. |
|
1 |
А |
||
2. |
Касание плоскости или поверхности. |
1 |
А |
|||
3. |
Прохождение плоскости образующей через |
2 |
в, |
|||
|
данную прямую. |
|
|
|
|
в2 |
• 4. |
Параллельность |
плоскости образующей |
2 |
|||
|
данной плоскости или поверхности. |
|
|
|||
|
|
|
||||
|
Перпендикулярность |
плоскости |
образую |
2 |
в, |
|
5. |
||||||
|
щей данной прямой. |
|
|
|
вА |
|
6. |
Перпендикулярность |
плоскости |
образую |
1 |
||
|
щей данной плоскости. |
|
|
|
в5 |
|
7. |
Касание плоскости образующей данной по |
2 |
||||
|
верхности по прямой. |
|
|
|
|
|
8. |
Касание плоскости образующей данной по |
1 |
в(, |
|||
|
верхности в точке. |
|
|
|
|
|
9. |
Пересечение с прямой или кривой в данной |
2 |
А |
|||
|
точке. |
|
|
|
! |
|
Комбинируя различные условия, некоторые из которых могут быть кратными, получаем все варианты образования поверхностей. При этом суммарная размерность условий должна быть равна пяти для окружности, шести - для параболы и семи для остальных кривых второго порядка. Но этого требования недостаточно. Дело в том, что необходимо учитывать, что все эти кривые - плоские. Поэтому сум марная размерность условий группы А не может превышать трех для
194
(жружности, четырех - для параболы и пяти - для эллипса и гипербо лы.
Суммарная размерность условий группы В не может превышать двух для всех кривых.
Таким образом, имеем следующие зависимости для образования
поверхностей: (ЕЛ)" |
где а = 3, р = 2 - для циклических по |
верхностей; а = 4, р = 2 |
- для параболических поверхностей; а = 5, |
В = 2 - для эллиптических и гиперболических поверхностей. Рассмотрим их образование в общем виде.
1) Сочетание условий Ах -Вь А]3 В5 дает циклические поверхно сти общего вида.
Частными видами таких поверхностей являются торы, число ви дов которых бесконечно велико. Они образуются в случае, если все
три кривые в условиях А? представляют собой центральные кривые с центрами, расположенными на прямой, через которую проходят плоскости по условию By .
Если кривые будут, например, винтовыми линиями, то образуют ся винтовые торы.
Условие Л, • Bs аналогично.
Условие А^-Ву или Ау5-В5 позволяет образовать эллиптические торы (образующая есть эллипс).
33
2)Условие А, • В2, А(-Щ позволяет построить циклические по
верхности |
с плоскостью параллелизма. |
Условие Ах5 -В2, Д5 -В3 по |
верхности |
с плоскостью параллелизма, |
несущие множество эллипсов |
или гипербол.
3)Условия, приведенные в п. Г) и 2) могут быть преобразованы
вусловия А\-Ву, А2-В3, А\-Вх, А2-В5, А\-В2, А\-Въ, А2-В2, А\-Въ.
Получающиеся поверхности будут того же вида.
Итак далее.
В частном случае, когда образующая имеет центр или вершину, условие Ау или А2 может быть заменено условием инцидентности центра или вершины какой—либо данной кривой.
Рассмотрим пример. Построить цилиндрическую поверхность, заданную условием Ау- А2-В2, радиус образующей окружности по стоянный. 195
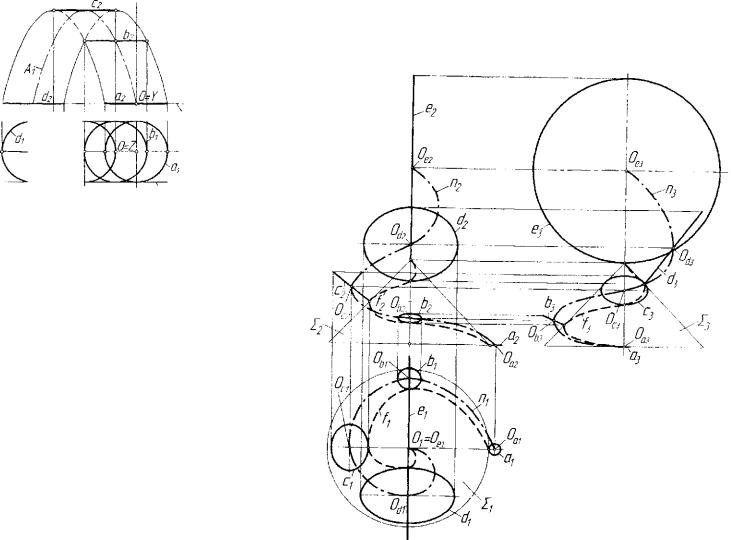
В |
качестве кривой, фигу |
|
Z |
|
||||||
рирующей в условии |
Ах, выбе |
|
|
|
||||||
рем |
параболу. |
В |
качестве |
|
|
|
||||
плоскости условия А2 выберем |
|
|
|
|||||||
плоскость |
|
этой |
|
параболы. |
|
|
|
|||
Пусть эта плоскость будет па |
|
|
|
|||||||
раллельна |
плоскости |
0X7. |
В |
|
|
|
||||
качестве |
плоскости |
паралле |
X- |
± |
'7 |
|||||
лизма |
условия |
В2 |
выберем |
|
||||||
|
|
|||||||||
плоскость |
|
OXY. |
Получается |
|
|
|||||
поверхность, |
изображенная |
на |
х~ |
|
||||||
рисунке 6.12. Эта циклическая |
|
|
||||||||
поверхность |
имеет |
название |
|
А*2 |
||||||
поверхности |
переноса. |
Изо |
|
|
|
|||||
бражены |
некоторые |
образую |
|
У |
|
|||||
щие этой поверхности - ок |
|
Рис. 6.12. Циклическая |
|
|||||||
ружности |
а, |
Ь, с, |
d. |
|
|
|
|
поверхность переноса |
|
|
Следующим примером будет циклическая поверхность, опреде ленная условиями касания образующей окружности переменного ра диуса заданного прямого кругового конуса 2" (рис. 6.13). Изменение радиуса от минимального (окружностьа(ах,а7,а-.)) до максимального (окружность е(ех,е2,е3)) происходит пропорционально высоте точки касания от основания конуса. Образующая окружность изменяет угол наклона своей плоскости к плоскости основания конуса пропорцио нально высоте точке касаттия от 0° до 90°. Касание конуса окружно стью происходит но конической винтовой линии f(fx,f2,f3) • Линией центров образующих окружностей служит спиралеподобная линия
п(пх,п2,щ).
Поэтому условие, задающие поверхность, могут быть записаны в виде Ау А1 -В5. Не смотря на то, что суммарная размерность этих ус ловий равна четырем, еще одно одномерное условие заключено в за коне пропорционального изменения радиуса образующей.
Другим примером может служить поверхность, образованная однопараметрическим множеством парабол, плоскости которых прохо
дят через |
ось |
OY, вершины |
принадлежат |
заданной параболе |
|
р(Р], р2,/?3); |
оси |
парабол лежат в |
плоскости |
0X7 |
(рис. 6.14). На ри |
сунке показаны образующие параболы а, Ь, |
с, d. |
|
|||
|
|
|
196 |
|
|
Рис. 6.13. Циклическая поверхность, определенная условиями А\ • А2-В,
197
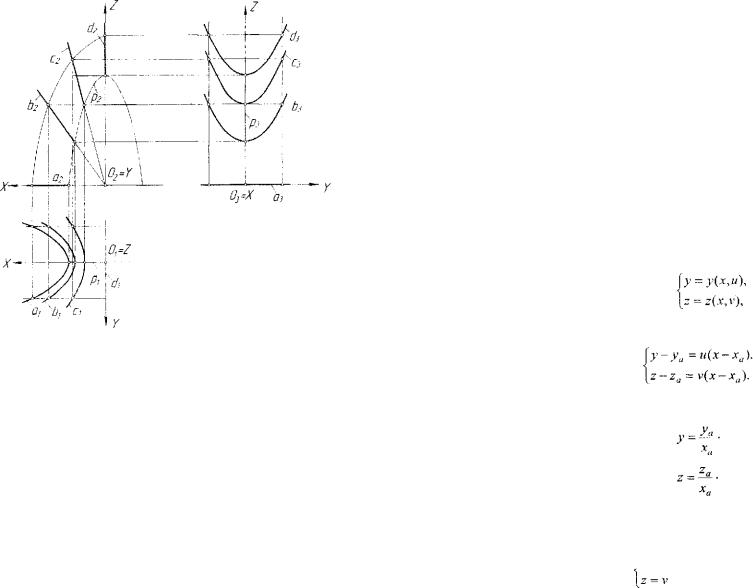
Рис. 6.14. Поверхность однопараметрическо! о множества парабол
6.3.Аналитические модели поверхностей
Интересной и достаточно сложной задачей является получение уравнений поверхностей в явном, неявном или параметрическом ви де. Как уже было отмечено, поверхность есть однопараметрическое множество линий. Поэтому такое множество можно описать аналити чески. Начнем с простых множеств.
В общем случае однопараметрическое множество линий описы вается уравнениями
\y |
= |
y(x,t), |
\z |
= |
z(x,t), |
представляющими собой уравнения семейств проекций линий на плоскости OXY и OXZ. Например, легко можно убедиться, что урав нения у = ах, z = bx описывают пучки прямых в плоскости OXY и
OXZ. Если а и b, произвольны, то оба уравнения опишут связку плоскостей с центром в начале координат. Если a-- f{b), то уравне ния опишут пучок таких плоскостей. Если а = Ь, то это будет пучок плоскостей, равнонаклоненных к плоскостям OXY и OXZ.
|
Однопараметрическое |
множество прямых с |
центром А(ха,уа), |
||
т.е. |
пучок прямых, |
описывается |
уравнением |
y-ya=t(x-xa). Если |
|
t - |
z, то уравнение |
у-уа |
= z(x-xa) |
опишет прямую |
линейчатую по |
верхность - прямой закрытый геликоид, ось которого параллельна
оси OZ |
и проходит через точку А. Если z - |
f(t), то |
получим прямой |
|
коноид общего вида. |
|
|
|
|
Однопараметрическое множество окружностей с центром в точке |
||||
В(хь,уь) |
описывается уравнением |
(x-xb)2 |
+(у-уь)2 |
-t2. |
Если t - z, то будет образован прямой круговой конус с осью в |
||||
точке В |
и с вертикальной осью. Если |
t = г2, то будет образован пара |
||
болоид с той же осью. И так далее.
Двухпараметрическое множество линий может быть описано системой уравнений
где и и v - параметры. Например, связка прямых с центром в точке A(xa,ya,za) описывается системой
Связка параллельных прямых, т.е. прямых параллельных направ лению OA, может быть задана уравнениями
|
х + и, |
|
X + V. |
Однопараметрическое множество пучков прямых, параллельных |
|
плоскости |
OXY, центры которых лежат на пространственной кривой |
/: у = у(х), |
z = Z ( J C ) , может быть записано в виде |
|
\у - у{х) = u(z - z(x)), |
198 |
199 |
|
