
1580
.pdf
y
B
H
M
C
A
o x
Для нахождения уравнения сторон треугольника воспользуемся
уравнением прямой, проходящей через две точки: |
x x1 |
|
|
y y1 |
. |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x1 |
y2 y1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(АВ): |
|
x 3 |
|
|
y 1 |
|
|
или |
|
x 3 |
|
|
|
|
y 1 |
|
|
– уравнение прямой АВ. |
|
|
||||||
|
|
|
7 1 |
|
|
|
6 |
|
|
|||||||||||||||||
|
1 3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
(АС): |
x 3 |
|
y 1 |
или |
|
x 3 |
|
|
y 1 |
|
– уравнение прямой АС. |
|
|
|||||||||||||
|
|
3 1 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
6 3 |
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
(ВС): |
x 1 |
|
|
y 7 |
|
или |
x 1 |
|
|
y 7 |
– уравнение прямой ВС. |
|
|
|||||||||||||
|
|
3 7 |
|
|
|
|
|
|||||||||||||||||||
|
|
6 1 |
5 |
|
|
|
|
4 |
|
|
||||||||||||||||
Пусть АН – высота, опущенная из вершины А на сторону ВС. Най-
дем ее уравнение в каноническом виде: x x0 y y0 . Так как высо- m n
та опущена из точки А, то x0 xA 3; y0 yA 1. Для нахождения
координат направляющего вектора s m,n воспользуемся |
уравне- |
||||
нием стороны ВС. |
Приведем его к общему виду 4(x 1) 5(y 7), |
||||
откуда 4x 5y 39 0. Так как AH BC , то нормаль n |
к пря- |
||||
мой ВС может рассматриваться как направляющий вектор s |
прямой |
||||
АН, т.е. m 4;n 5. |
|
||||
Имеем |
x 1 |
|
y 7 |
– уравнение высоты АН. |
|
|
|
|
|||
|
4 |
5 |
|
||
Пусть АМ – медиана, проведенная из вершины С на сторону АВ. По определению медианы, точка М делит отрезок АВ пополам. Координаты середины отрезка находим по формулам
39

|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
xA xB |
|
|
|
3 1 |
|
|
2; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yA |
|
yB |
|
|
|
|
|
1 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
yM |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для нахождения уравнения медианы СМ воспользуемся уравне- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нием прямой, проходящей через две точки: |
|
|
|
x x1 |
|
y y1 |
. Так как |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x2 x1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 y1 |
||||||||||||
С(6,3), M(2,4), то |
|
x 6 |
|
y 3 |
|
|
или |
x 6 |
|
|
|
y 3 |
– уравнение медианы |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
СМ. |
|
|
|
|
|
2 6 |
|
|
4 3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Расстояние от вершины С до стороны АВ находим по формуле |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d |
|
|
Ax0 |
By0 C |
|
|
. Так как 6x 2y 20 0– общее уравнение сторо- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
A2 B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ны АВ, |
то А=6; В=2; С= –20; x0 xC 6; y0 yC 3. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d |
|
6 6 2 3 20 |
|
|
|
|
|
|
22 |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
36 4 |
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Угол между сторонами АВ и АС равен углу между векторами AB |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и AC. Для точек A(3,1), B(1,7),С(6,3) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
AB 1 3;7 1 2;6 , |
AC 6 3;3 1 3;2 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
cos |
|
AB |
|
AC |
|
|
|
|
2 3 6 2 |
|
|
|
|
|
|
|
6 |
|
|
|
. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
AB |
|
AC |
|
|
4 36 |
|
|
|
9 4 |
40 |
13 |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Искомый угол между сторонами АВ и АС будет равен |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccos |
|
|
|
|
|
6 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для вычисления периметра треугольника АВС сложим длины всех его сторон: Р АВ АС ВС .
Так как AB 2;6 , AC 3;2 , ВC 5; 4 ,
то АВ 
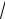 4 36
4 36 
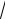 40,
40,
АС 
 9 4
9 4 
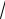 13; ВС
13; ВС 
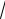 25 16
25 16 
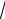 41.
41.
Тогда периметр треугольника Р 
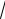 40
40 
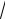 13
13 
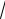 41. 2. Назвать кривые, построить.
41. 2. Назвать кривые, построить.
40
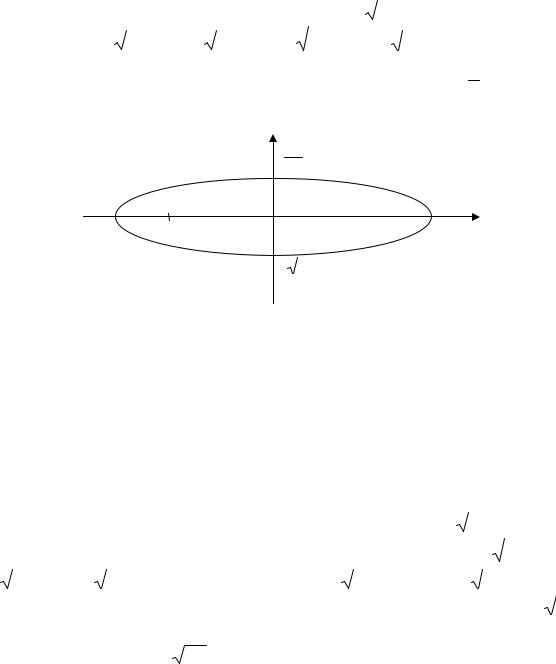
а) 24x2 49y2 1176.
Решение. Для построения кривой приведем ее уравнение к каноническому виду. Для этого разделим обе части равенства на 1176. Име-
|
x2 |
|
y2 |
|
|
|
|
|
|
||||||
ем |
|
|
|
|
1 – каноническое уравнение эллипса с центом в точке |
||||||||||
49 |
|
24 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
О(0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Параметры эллипса: |
|
|
|
|
|
|
||||||||
|
Большая полуось а=7, малая полуось b= |
|
24 |
|
. Вершины эллипса: |
||||||||||
(7,0), (-7,0), (0, |
|
), (0, - |
|
); с |
a2 b2 |
|
|
|
5. Фокусы |
||||||
24 |
24 |
|
49 24 |
||||||||||||
эллипса F1(5,0) и F2(–5,0). Эксцентриситет эллипса 5 .
7
П о с т р о е н и е .
y

 24
24
|
F2 |
|
|
F1 |
|
|
-7 |
-5 |
0 |
|
|
7 x |
|
5 |
||||||
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
б) 24x2 49y2 1176.
Решение. Для построения кривой приведем ее уравнение к каноническому виду. Для этого разделим обе части равенства на 1176. Име-
ем |
|
x2 |
|
y2 |
|
1 – каноническое уравнение гиперболы с центром в |
||||||||||||
49 |
|
|
|
|||||||||||||||
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
точке О(0,0). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Параметры гиперболы: |
|
|
|
|
|
|
|
||||||||||
|
Действительная полуось а=7, мнимая полуось b= |
|
|
. Вершины |
||||||||||||||
|
24 |
|||||||||||||||||
гиперболы: (7,0), (–7,0). Найдем фокальное расстояниес |
|
a2 b2 |
. |
|||||||||||||||
|
|
|
|
|
. Фокусы гиперболы F1( |
|
, 0) и F2 (– |
|
|
, 0). Раз- |
||||||||
49 24 |
|
73 |
73 |
73 |
||||||||||||||
меры основного прямоугольника гиперболы2а 2b |
14 2 |
|
. |
|||||||||||||||
24 |
||||||||||||||||||
Его диагонали лежат на асимптотах гиперболы, определяемых урав-
нениями y |
b |
x |
24 |
x. |
|
7 |
|||
|
a |
|
||
41
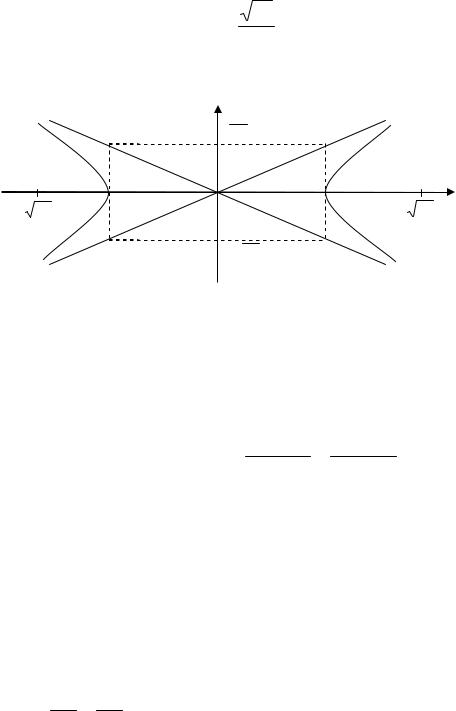
Эксцентриситет гиперболы 73 . 7
П о с т р о е н и е .
y

 24
24
F
2
F2 |
|
|
|
F1 |
- 73 |
-7 |
0 |
7 |
73 x |

 24
24
в) 4x2 y2 16x 4y 0.
Решение. Имеем общее уравнение кривой 2-го порядка. Так как А=4; С=1; В=0; A C 0 , то имеем эллипс.
Преобразуем уравнение 4(x2 4x) (y2 4y) 0;
4(x2 2 2x 22) 4 22 (y2 2 2y 22) 22 0;
4(x 2)2 (y 2)2 20; (x 2)2 (y 2)2 1 5 20
– каноническое уравнение эллипса с натным осям и координатами центра перенесем начало координат в точку
осями, параллельными коорди- (–2,2). Для построения кривой (–2,2), т.е. сделаем замену
x x x0 x 2;
y y y0 y 2.
В системе координат Ox y уравнение кривой будет иметь кано-
нический вид x 2 y 2 1.
520
По с т р о е н и е.
42
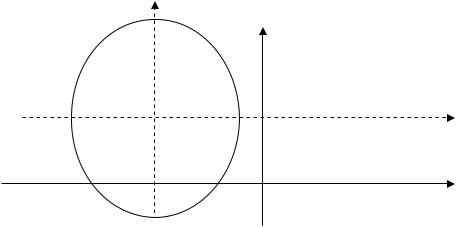
y
y
2 x
-2 |
-1 0 |
x |
3. Найти расстояние от точки M0 2; 3;1 до плоскости, проходящей
через три точки:M1 1;1; 1 , |
M2 3;2; 4 , |
M3 2;1;0 . |
Решение. Составим уравнение плоскости, проходящей через три точ-
ки M1, M2, M3:
|
x 1 |
y 1 |
z 1 |
|
|
||
|
|
||||||
|
3 1 |
2 1 |
4 1 |
|
0 |
||
|
2 1 |
1 1 |
0 1 |
|
|
||
или |
|
|
|
|
|
||
|
|
x 1 |
y 1 |
z 1 |
|
|
|
|
|
|
|
|
|||
|
2 |
1 |
5 |
0. |
|||
|
1 |
0 |
1 |
|
|
|
|
Вычисляем определитель, раскладывая по первой строке:
x 1 |
1 |
5 |
y 1 |
2 |
5 |
z 1 |
2 |
1 |
0; |
|
0 |
1 |
|
1 |
1 |
|
1 |
0 |
|
1 x 1 3 y 1 1 z 1 0; x 1 3y 3 z 1 0;
x 3y z 5 0 уравнение плоскости, проходящей через точки M1,
M2, M3.
Теперь используем формулу расстояния от точки до плоскости:
43

d |
|
2 3 3 1 5 |
|
|
2 9 6 |
|
13 |
|
13 |
|
|
13 |
11 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
12 32 1 2 |
11 |
|
11 |
|
|
11 |
|
|
11 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 13 11 расстояние от M0 до плоскости. |
|
11 |
|
4. Написать уравнение плоскости, проходящей через точку A перпен- |
|
дикулярно вектору BC, если A 2;3; 2 , B 3;1; 4 , |
C 1; 1; 2 . |
Решение. Найдём координаты вектора BC:
BC 1 3; 1 1; 2 4 2; 2; 2 .
Получившиеся числа являются коэффициентами перед x, y, z в уравнении плоскости , перпендикулярной BC :
: 2x 2 y 2z B 0.
По условию, точка A принадлежит , координаты A удовлетворяют уравнению плоскости:
2 2 2 3 2 2 B 0;
4 6 4 B 0;
B 14.
Уравнение : 2x 2 y 2z 14 0 или x y z 7 0.
Ответ: : |
2x 2 y 2z 14 0 или x y z 7 0. |
|
5. Найти |
угол между плоскостями |
x y 3z 4 0 и |
2x y z 8 0.
Решение. Угол между плоскостями совпадает с углом между их нор-
малями. Нормали плоскостей: |
n1 1, 1, 3 ; |
n |
2 2,1, 1 . |
|
|
|
|
|
|
|||||||||||||||||||||
Угол между нормалями найдём с помощью скалярного произве- |
||||||||||||||||||||||||||||||
дения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
cos |
n1 |
|
n2 |
|
|
|
|
2 1 1 1 3 1 |
|
|
|
|
|
2 |
|
|
2 |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n1 |
|
n2 |
12 1 2 32 |
|
|
22 12 1 2 |
11 6 |
66 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: cos |
|
|
|
|
|
|
; arccos |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
66 |
|
|
|
|
66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6.Написать каноническое уравнение прямой:
x y 3z 4 0;
x y z 1 0.
44

Решение. Чтобы составить каноническое уравнение прямой, необходимо найти её направляющий вектор и точку на прямой.
Направляющий вектор прямой a находим как векторное произведение векторов-нормалей плоскостей: a n1 n2.
n1 1,1, 3 ; n2 1,1,1 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
k |
|
|
|
1 |
3 |
|
|
|
1 |
3 |
|
|
|
1 |
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a |
|
n1 |
n |
2 |
1 1 |
3 |
i |
j |
k |
|
||||||||||||||||||||
1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||||||||
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4i 4 j 0k 4i 4 j 4; 4;0 .
Найдём какую-нибудь точку на прямой. Положим, например, y 0. Тогда получим систему
x 3z 4 0;
x z 1 0;
4z 5 0;
z 5. 4
Тогда x 5 1 0; x 1.
4 |
4 |
|
|
|
||
|
|
1 |
|
5 |
|
|
Итак, получили точку |
|
|
;0; |
|
. |
|
4 |
4 |
|||||
|
|
|
|
|||
Составляем каноническое уравнение прямой:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5 |
|
|
||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
4 |
y 0 |
|
z 4 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
5 |
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
y |
z |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||
|
x |
|
|
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
4 |
|
|
4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. Найти точку пересечения прямой и плоскости:
x 1 |
|
y 1 |
|
z 3 |
; |
x 2 y z 1 0. |
2 |
|
|
||||
4 |
1 |
|
|
|||
45

Решение. Запишем уравнение прямой в параметрическом виде:
x 1 y 1 z 3 t
2 |
4 |
1 |
x 1 2t; |
|
x 2t 1; |
|
|
|
y 1 4t; или |
y 4t 1; |
|
|
|
|
z 3 t |
|
z t 3. |
Подставляем эти выражения в уравнение плоскости:
2t 1 2 4t 1 t 3 1 0;
2t 1 8t 2 t 3 1 0;
5t 1 0; t 1.
Подставляем в систему: |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
7 |
|
|||||||
x 2 |
|
|
|
|
|
1 |
|
; |
||||
|
|
|||||||||||
|
|
|
5 |
5 |
|
|||||||
|
|
|
1 |
1 |
|
|
||||||
y 4 |
|
|
|
|
|
1 |
|
; |
||||
|
|
|
||||||||||
|
|
|
5 |
5 |
|
|
||||||
z |
1 |
3 |
14 |
. |
||||||||
|
|
|||||||||||
|
5 |
|
|
|
5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
Итак, нашли координаты точки пересечения: |
|
7 |
; |
1 |
; |
14 |
. |
||||||||
|
|
|
5 |
||||||||||||
|
|
|
|
|
|
|
|
5 |
|
5 |
|
||||
Ответ: |
7 |
; |
1 |
; |
14 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||
5 |
|
5 |
|
|
|
|
|
|
|
|
|
||||
РАЗДЕЛ 4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
4.1. Типовой расчет
1 . Задания по теме «Комплексные числа»:
а) представить комплексное число в показательной форме, изобразить на комплексной плоскости;
46

б) выполнить действие и результат записать в показательной форме;
в) найти все корни, сделать проверку для одного корня; г) выполнить действие, результат записать в показательной
форме и изобразить полученное число точкой на комплексной плоскости;
д) найти корни уравнения, сделать проверку.
2. Найти пределы числовых последовательностей или установить их расходимость.
3. Найти пределы функций.
4. Исследовать функцию на непрерывность. Установить тип точек разрыва и изобразить график функции в окрестности этих точек.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант № 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; г) 3,21e8,180 j |
|
2,24e |
24,720 j |
|
|
||||||||||||||||||||||||
1. а) |
|
z 2j ; |
б) |
; |
|
в) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
2j |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
j |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 j |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,17e 31,41 |
|
|
||||||||||||||
д) 2x2 6x 5 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2. а) |
1; |
1 |
; |
1 |
|
; ; |
( 1)n 1 |
|
; ; б) |
a |
n |
|
n 1 |
|
|
; в) a |
n |
|
n! |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 4 |
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4n 3 |
|
|
|
|
|
|
|
|
cosn |
|
|
|
|
|
||||||||||||||||||||||
3. а) |
lim |
|
3x2 4x 2 |
; б) |
lim |
|
|
|
|
2x |
2 5x |
|
; в) lim |
|
|
x2 |
1 |
|
|
; |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
x x2 6x 5 |
|
|
|
|
|
|
|
x 3x3 |
5x 1 |
|
x 1 x2 6x 7 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
x3 1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
ctg2x |
|
|||||||||||||||
г) |
lim |
|
|
|
; д) |
lim |
|
|
|
|
x |
x |
|
|
|
; е) |
lim |
|
|
|
|
|
; |
|
ж) lim |
; |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
x2 4 |
|
|
x 0 3 |
|
x2 |
6 |
|
x |
|
|
|
|
|
|
x 0 sin5x |
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
x 3 |
x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
)x ; к) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
з) |
|
|
|
|
|
|
|
|
|
; и) lim(1 |
|
|
|
lim |
3x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
x x 2 |
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. а) f (x) |
|
|
|
|
|
|
|
; б) f (x) |
x3, |
0 x 2; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
x 2. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 x
47

Вариант № 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,80 j |
|
1,28e 71,210 j |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1. а)z 2 2 3j; б) |
|
|
|
|
|
|
|
; в) |
|
3 2 2 |
|
3j ; г) 2,48e |
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||||||||||||||||||||||||||||||||
5 j |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
j |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,45e5,41 |
|
|||||||||
д) x2 4x 5 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2. а) 1; |
|
|
|
; |
|
; ; |
|
|
; ; б) an |
|
|
|
|
|
|
|
|
|
; в) |
an |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4n 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
4 |
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosn |
|
|
|
|
|
|
|
|
||||||||||||||||||
3. а) lim |
3x |
2 |
4x 2 |
; б) |
lim |
|
2x2 5x 8 |
|
; в) |
lim |
|
|
x |
2 |
|
1 |
|
; |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
5x |
2 |
7 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2x 3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
x 6x2 x 5 |
|
|
|
|
|
|
x 3x |
|
|
|
|
|
|
|
x 1 x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
x2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
|
|
|
|
|
|
|
|
ctg4x |
|
|
|
||||||||||||||||||||
г) |
|
|
|
; д) |
|
|
|
|
|
|
|
|
x |
x |
|
; е) lim |
|
; |
|
ж) |
|
|
|
|
; |
|
|
|||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x |
|
x 2 |
|
|
|
x 0 3 x4 6 |
|
x |
|
|
|
x 0 tg5x |
|
|
|
|
x |
|
|
|
5x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
x 3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
)x; к) lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
з) |
; и) lim(1 |
5x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
x x 3 |
|
|
|
|
x 3 |
|
|
|
|
|
x |
|
|
|
|
|
|
x 2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
3x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2, x 0; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
4. а) f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; б) f (x) 4e |
|
, 0 x 4; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
x2 |
4x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
x 4. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x 4
Вариант № 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,180 j |
|
|
|
2,24e24,720 j |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1. а) |
z 1 |
|
|
|
3j; б) |
|
|
|
|
|
|
3 1 3j ; г) 3,21e |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 j |
|
; в) |
|
|
|
; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1,17e 31,410 j |
|||||||||||||||||||||||||||||||||||||||||||||||
д) x2 2x 2 0. |
( 1)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2. а) |
1; |
|
1 |
; |
|
1 |
|
; ; |
|
; ; б) an |
n 1 |
|
; в) an |
|
|
n |
. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
3 |
9 |
|
3n 1 |
|
n2 3 |
cosn |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3. а) |
lim |
|
|
x2 x 2 |
; б) |
|
lim |
|
2x4 |
5x 8 |
|
; в) lim |
|
x2 x 2 |
; |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x 4x2 x 5 |
|
|
|
|
x 3x2 |
|
|
|
|
|
x 1 x2 6x 7 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
4 |
x3 |
x |
|
|
|
|
|
|
|
|
|
|
|
12 |
x5 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
ctg2x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
г) lim |
|
|
|
|
|
|
|
|
|
|
; д) lim |
|
|
|
|
|
|
|
|
|
|
|
; е) lim |
|
|
|
|
|
|
; |
|
ж) lim |
|
|
|
|
|
; |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctg3x |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x |
x2 |
|
4 |
|
|
|
|
x 0 3 |
|
x2 4 |
x |
|
|
|
x 2 sin5x |
|
|
x |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
48
