6. yV yIV 2x 3.
dx
2x y;
7. dt
dy 14x 3y.
dt
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №10 |
|
1. x |
|
|
dx y |
|
|
dy 0. |
|
5 y2 |
4 x2 |
|
|
|
|
|
xy |
|
|
x |
|
|
2 |
|
|
2. y |
21 x2 |
2; |
y 0 3. |
|
|
3.y ctg2x 2y .
4.y 4y 4y 0; y(2) 4; y (2) 0.
5. а) y 5y 4xe5x ; |
б) y 5y 4x 3. |
6. |
yIV |
2y y 4x2 . |
|
|
dx |
|
7. |
|
|
|
|
3x y; |
|
|
|
|
dt |
|
|
|
|
|
|
dy |
4x y. |
|
|
|
|
|
|
|
dt |
|
|
|
|
Вариант №11
1.y 4 ex dy exdx 0.
2.y xy x3; y 0 3.
3.x4 y x3 y 1.
4.y 8y 16y 0; y(0) 1; y (0) 2.
5. а)y 6y 13y e4x (x 3); |
б) y 6y 13y 6x 5. |
6. |
yIV |
4y 4y x x2 . |
|
|
dx |
|
7. |
|
|
|
|
3x y; |
|
|
|
|
dt |
|
|
|
|
|
|
dy |
3x y. |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №12 |
1. |
|
|
|
|
|
y xy2 x 0. |
|
|
|
|
4 x2 |
|
|
2. |
|
|
|
|
2xy |
2 |
, y 1 3 |
|
|
y |
|
|
|
|
|
1 x |
|
; |
|
|
|
1 x2 |
|
|
3. |
xy 2y 0. |
|
|
|
|
4. |
y 3y 2y 0; |
|
y(0) 1; y (0) 1. |
5. а)y 4y 3y (x2 2)ex ; |
б) y 4y 3y x2 2. |
6. |
y y 6x2 3x. |
|
|
|
dx |
|
x 2y; |
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dy |
|
2x 5y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
Вариант №13
1.2xdx 2ydy x2 ydy 2xy2dx.
2.y 1 2x y 1; y 1 1.
x2
3.1 x2 y 2xy x3 .
4. |
y 6y 10y 0; |
y(0) 1; y (0) 0. |
5. |
а)y y y 3xe2x ; |
б) y y y 3x2 2. |
6. |
yIV |
3y 3y y 2x. |
|
|
dx |
|
|
7. |
|
|
|
|
x 4y; |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dy |
2x 3y. |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
Вариант №14
1. x
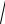 4 y2 dx y
4 y2 dx y
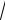 1 x2 dy 0.
1 x2 dy 0.
3. x5y x4 y 1.
4. |
25y 20y 4y 0; |
y(0) 2; y (0) 1. |
5. а) y 2y 5y (x2 1)ex; |
б) y 2y 5y x2 1. |
6. |
yIV |
2y y 2x 1 x . |
|
|
dx |
|
|
7. |
|
|
|
|
5x 4y; |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
dy |
2x 11y. |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
Вариант №15
1. ex 8 dy yexdx 0.
y12
2.y x x3 ; y 1 4.
3.xy y 1 0.
x
4. |
2y |
|
5y |
|
|
|
|
|
|
2y 0; y(0) 0; y (0) 2. |
|
5. |
а)y y 12y (x2 1)ex ; |
б) y y 12y x2 |
14. |
6. |
y 5y 6y x 1 2 . |
|
|
dx x 7y;
7. dt
dy x 5y.
dt
Вариант №16
1.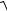
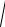 5 y2 y y
5 y2 y y
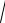 1 x2 0.
1 x2 0.
2.y 2 y x3; y 1 5.
x6
3.xy y x 0.
4. y 2y y 0; y(0) 2; y (0) 4.
5.а)y 6y 5y 3cosx; б) y 6y 5y 3x2 4x 22.
6.y 13y 12y 18x2 39.
Вариант №19
1. 1 ex y yex.
2. y y x 1ex; y 1 e.
xx
3.y tg x y 1.
|
|
|
|
|
|
|
|
|
|
4. |
y |
|
2 2y |
|
2y 0; |
|
|
|
|
y(0) 1; y (0) 0. |
5. а)y 2y 3y 4xex ; |
б) y 2y 3y 4x3 2. |
6. |
y 13y 12y x 1. |
|
|
dx |
|
|
|
|
7. |
|
|
|
|
x 3y; |
|
|
|
|
|
|
dt |
|
|
|
|
|
|
dy |
6x 4y. |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
Вариант №20
1.
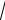 1 x2 y xy2 x 0.
1 x2 y xy2 x 0.
2.y y 2lnx; y 1 1.
xx
3.y tg5x 5y .
4. |
9y 12y 4y 0; |
y(0) 0; y (0) 1. |
5. а)y 7y 12y x2 e3x ; |
б) y 7y 12y x2 2x 6. |
6. |
y y 6x 5. |
|
|
|
dx |
|
5x y; |
|
|
7. |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
dy |
|
3x 9y. |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
Вариант №21
1.6xdx 2ydy 2yx2dy 3xy2dx.
2.y y sinx; y 1 .
3.4y3y y4 1.
4. |
y 2y 8y 0; y(2) 1; |
y (0) 5. |
5. а)y 5y 4y 4x2 e2x ; |
б) y 5y 4y 4x2 3x. |
6. |
y y 3x2 2x 1. |
|
|
dx |
|
7x 3y; |
|
7. |
|
|
|
|
|
|
dt |
|
|
|
|
|
dy |
|
5x y. |
|
|
|
|
|
|
dt |
|
|
|
Вариант №22
1.y 1 ln y xy 0.
2.y y x2; y 1 1.
2x
3.y 128y3.
4.y 4y 0; y(0) 0; y (0) 2.
5. а) y 2y y e2x(sin2x cos2x); |
б) y 2y y 3x 4. |
6. |
yIV |
|
3y 3y y x 3. |
|
|
dx |
|
6x 4y; |
|
7. |
|
|
|
|
|
|
dt |
|
|
|
|
|
dy |
|
2x y. |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №23 |
|
1. 3 ex yy ex. |
|
|
|
|
|
|
|
|
|
|
2x |
|
2x2 |
|
|
2 |
|
|
2. |
y |
1 x2 |
y 1 x |
2 ; y 0 3. |
|
|
|
3. |
|
|
|
3 |
64. |
|
|
|
|
|
y y |
|
|
|
|
|
|
4. |
y 2y 10y 0; |
y(0) 0; y (0) 1. |
5.а) y 2y 2y 7xex ; б) y 2y 2y 7x 2 3x 1.
6.y 4y 32 384x2 .
dx
5x 3y;
7. dt
dy x y.dt
Вариант №24
1. 
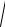 3 y2
3 y2 
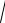 1 x2 yy 0.
1 x2 yy 0.
2. y |
y |
x2 2x; y 1 |
3 |
. |
x 2 |
|
|
2 |
|
3.y 2sin ycos3 y 0.
4.2y 5y 2y 0; y(0) 0; y (0) 1.
5.а) y 12y 36y ex sin3x; б) y 12y 36y 4x2 3x 7.
6.3yIV y 6x 1.
dx |
|
6x y; |
|
|
|
|
7. dt |
|
|
|
dy |
|
7x 2y. |
|
|
|
dt |
|
|
Вариант №25
1. xdx ydy yx2dy xy2dx.
x1
3.y 32sin3 ycosy.
4.y 5y 4y 0; y(0) 5; y (0) 8.
5. а) y 5y 6y (4x 5)ex ; |
б) y 12y 36y 6x2 x 5. |
6. |
y y 5x2 1. |
|
|
dx |
|
8x 7y; |
|
7. |
|
|
|
|
|
|
dt |
|
|
|
|
|
dy |
|
2x y. |
|
|
|
|
|
|
dt |
|
|
|

8.2. Пример выполнения типового расчета
Решить дифференциальные уравнения и системы дифференциальных уравнений. Если указано начальное условие, решить задачу Коши.
1. tgxsin2 y dx cos2 x ctg ydy 0.
Решение. Это дифференциальное уравнение первого порядка с разделяющимися переменными. Обе части уравнения разделим на
sin2 y cos2 x 0(по ОДЗ уравнения), |
получим |
sinx |
dx |
cos y |
dy. |
cos3 x |
|
|
|
|
|
|
|
|
|
sin3 y |
Проинтегрировав обе части уравнения, найдем общее решение |
|
1 |
|
|
1 |
|
C. |
|
|
|
|
cos2 x |
sin2 |
|
|
|
|
|
|
y |
|
|
|
2. y tgx y cosx; y(0) 1.
Решение. Поставлена задача Коши. Дифференциальное уравнение является линейным, первого порядка. Полагаем y u . Тогда уравнение принимает вид
u tgx u u cosx. |
(2) |
Найдем u из условия |
|
u tgx u 0. |
(3) |
Решая его, получим u 1 . Константу, возникающую при инcos x
тегрировании уравнения (3), здесь отбрасываем. Найденное значение
u подставляем в |
(2) |
и после преобразований |
имеем уравнение |
|
d |
cos2 |
x, откуда υ cos2 |
|
xdx |
1 |
x |
1 |
cos2x C. |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
Следовательно, общее решение исходного уравнения имеет вид |
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
y |
|
x |
|
|
cos2x |
C |
|
|
. Используем теперь начальное условие |
|
2 |
4 |
|
|
|
|
|
|
|
|
cosx |
|
|
1 |
|
3 |
|
для нахождения константы: |
y(0) 1: |
1 |
С; С |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
Следовательно, решение задачи Коши имеет вид

|
1 |
|
1 |
|
3 |
|
|
1 |
|
|
y |
|
x |
|
cos2x |
|
|
|
|
. |
|
2 |
4 |
4 |
cosx |
|
|
|
|
|
|
|
3. y y 0.
Решение. Это дифференциальное уравнение второго порядка, допус-
кающее понижение порядка. Применив подстановку y p; y p dp, dy
преобразуем уравнение к виду y dp ydy 0. Получили уравнение первого порядка с разделяющимися переменными. Общий интеграл этого уравнения имеет вид y 2 y2 С12. В получившемся дифферен-
|
циальном уравнении разделим переменные, получим |
|
|
dy |
|
dx. |
|
|
|
|
|
|
С2 y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
1 |
|
|
|
Интегрируя, находим |
решение arcsin |
x С2 |
, |
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
С1 |
|
|
|
|
y С1 |
sin x С2 . Знак включен в постоянную С1. |
|
|
|
|
|
|
Это общее решение исходного уравнения. Его можно преобразо- |
|
вать к виду |
|
y С3 sin x С4 cosx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где С3 |
С1 cosС2; |
С4 С1 sinС2. |
|
|
|
|
4. y |
|
6y |
|
7y 0; |
|
|
|
|
|
|
|
|
y(0) 2; y (0) 0. |
|
|
|
Решение. Поставлена задача Коши для линейного дифференциального однородного уравнения второго порядка с постоянными коэффициентами.
Ищем общее решение уравнения. Составляем характеристиче-
ское уравнение: t2 6t 7 0. Его решениями являются |
t 1; |
|
1 |
t2 7. Корни характеристического уравнения действительные, различные, поэтому общее решение дифференциального уравнения имеет вид
y C1ex C2e 7x .
Используем начальное условие y(0) 2. Подставляя в общее решение, получаем 2 C1 C2 .
Чтобы использовать условие на производную решения, продифференцируем общее решение:
y C1ex 7C2e 7x .
Теперь используем условие y (0) 0. Получаем уравнение
0 C1 7C2 .
Решаем систему получившихся уравнений
C1 C2 2;C1 7C2 0.
Находим решение системы C |
7 |
; C |
|
|
1 |
. Итак, решение задачи |
4 |
|
|
|
7 |
|
|
|
1 |
|
|
1 |
|
2 |
4 |
|
|
|
x |
|
|
7x |
. |
|
|
|
|
|
|
Коши имеет вид |
y |
|
e |
|
|
|
e |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
1
5. y 1 y 1 y 3e2x. 2 2
Решение. Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Характеристическое уравнение
t2 |
1 |
t |
1 |
0 имеет корни t |
|
1; t |
2 |
|
1 |
|
, так что общее решение со- |
|
|
|
|
|
2 |
2 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С ex С |
|
x |
ответствующего уравнения без правой части есть y |
|
|
0 |
e 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
Остается найти какое-либо частное решение исходного уравне- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
(А – постоян- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния. Частное решение будем искать в виде Y A e2 |
ная). |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляем Y A e2 в исходное уравнение, получаем |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
x |
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
A |
|
A e2 |
3e2 . |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, получаем A 6. |
Искомое |
|
Приравнивая коэффициенты при e2 |
1x
частное решение Y 6 e2 . Общее решение уравнения имеет вид





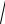

 5
5 
 1
1 

 x
x




 3
3 
 1
1 

