Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1580

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.35 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

2. Вычислить площадь, ограниченную кривыми 3x y 0; y 3;

3x 4y 0.

	1	3
3. Найти длину дуги кривой y		x2 2		;	2	x	7	.
			2

3

4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями y x3; x 0.

Вариант №5

1. Вычислить неопределенные интегралы.

		x		x				3
	2e	x	2	x

1								1 x2
		dx						1 x2
3.		dx			.
3.	sin2(4x)				.
	sin2(4x)
5.			6x 1						dx.
5.	(x 1)(x2								dx.
	(x 1)(x2						2)
7.			dx			.
7.						.
	1 cos2x

1 dx.

2.	(3tgx 7)	8 dx				.
			cos2
					x
4.	3x			dx.
	x2 4x 8

6. 23 x sin x dx .

8. 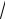xdx .

1 x

2.Вычислить площадь, ограниченную кривыми y x2 4x 5; x y 5 0.

3.Найти длину дуги кривой y 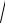x x2 arcsin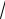x ; 0 x 1.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y 1 ; x 1; x 6. x

Вариант №6

1. Вычислить неопределенные интегралы.

		1
	3cosx 6sinx		2

1.		1 x2		dx.
		1 x2

3. 5x cos5xdx.

2. 37x 1dx.

4.	2x 1	dx.


	x2 4x

119

	5.	6x 1		dx.		6. (cos3x)x3dx.
	5.	(x 1)(x2		dx.		6. (cos3x)x3dx.
		(x 1)(x2	1)
		dx
	7.	dx			.	8.				6x 1				dx.

									3		6x 1
		1 sin x cosx							3		6x 1
2.	Вычислить площадь, ограниченную кривыми y2 2x;													x2 2y.
3.	Найти длину дуги кривой y ln 1 x2 ;						1	x				1	.
3.	Найти длину дуги кривой y ln 1 x2 ;							x					.
						2				2

4. Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y sinx; x .

Вариант №7

1. Вычислить неопределенные интегралы.

2 5

dx.

2. cos(31x 8)dx.

(5lnx 1)10

dx.

7x 1

dx.

x2 8x 12

7 4x2

dx.

6. arcsin

xdx.

(2 x2)(x 3)

cosx 2sinx

x 2

2.Вычислить площадь, ограниченную кривыми y x2 8x 16; x y 6 0.

3.Найти длину дуги кривой 9y2 x x 3 2 ; 0 x 3.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x3 ; y 2x. 4

Вариант №8

1. Вычислить неопределенные интегралы.

		x		2	1			dx
1.	3 7					dx.	2.			.
			x2	1	x2 1			sin2	(12x)

120

arctgx

dx.

2 x

dx.

1 x2

3 x2 2x

3x 1

dx.

6. (4x2 1)e3xdx.

(x 1)(x2

7. sin8 xdx.

x 1

2. Вычислить площадь, ограниченную кривыми

y 2x.

;

3. Найти длину дуги кривой y lncosecx;

4. Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x2 ; 2x 2y 3 0. 2

Вариант №9

1. Вычислить неопределенные интегралы.

1. (3sin x 2

x 3 x)dx.

2. (5cosx 7)4 sinxdx.

sin(4x 2)dx.

2x 1

dx.

5 x2 6x

dx.

6. (4x 8)e3xdx.

1)(x 6)

xdx

sin4

xcos4

xdx.

x 3 x

2. Вычислить площадь, ограниченную кривыми

2x 2y 3 0;

3. Найти длину дуги кривой y 1 x2 1ln x; 1 x e.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y 3sin x; y sin x; 0 x .

121

Вариант №10

1. Вычислить неопределенные интегралы.

	3			4		6

		2			2
1.				1 x		x2	1	dx.
sin			x

3. 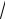cosx sinxdx.

2.	3dx		.

5 (7x)2
4.	5x			dx.

	6 x2
		x

5.	x 1	dx.	6. 23x cosxdx.
5.	(x 1)(x 3)(x 8)	dx.	6. 23x cosxdx.
	(x 1)(x 3)(x 8)			dx
7.	cos2 3xsin5xdx.		8.	dx	.


				x 7 1
				x 7 1

2.Вычислить площадь, ограниченную кривыми y x2 6x 9; y 3x 9.

3.Найти длину дуги кривой y arcsine x ; 0 x 1.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x3; y 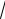x .

Вариант №11

1. Вычислить неопределенные интегралы.

1. (2sin x		3		7			)dx.
						x


			x
3. x53x6 2 dx.
5.	3x 1				dx.
	(x 5)(x2
		5)

7. cos3 3xsin5xdx.

2. cos(3x 1)dx.

4x 1

4. x2 2x dx.

6. x2 cos2 xdx..

8. 3x 4 8dx.

2.Вычислить площадь, ограниченную кривыми y2 x 2; x 0.

3.Найти длину дуги кривой y lnsecx; 0 x .

4. Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y tgx; x .

6 3

122

Вариант №12

1. Вычислить неопределенные интегралы.

			2				3			7
1.			2				3			7
					2
					2		x			11 x2	dx.
	x						x			11 x2
	5
3.	5			tgx 2					dx.
3.			cos2x						dx.
			cos2x					x 1
5.								x 1				dx.
5.												dx.
		(x 1)(x 3)(x 7)
7. cos2						3x sin2 4xdx.

2. xex2dx.

4. 4x x2 8dx.

6. (3x2 8)cos4xdx.

8.	2	x	1 1	dx.


		2x 1

2.Вычислить площадь, ограниченную кривыми y x2 6x 5; y 0.

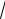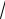3.Найти длину дуги кривой y ln x; 3 x 8.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

	x,	4 x 0;
ти, ограниченной линиями
	y
	sinx,	0 x		.
			2

Вариант №13

1. Вычислить неопределенные интегралы.

		2					5			3
1.												dx.
		1 x2			4 x2				6

											x
						dx.
3.			4tgx 1
3.			cos2 x
			cos2 x
5.			x 1					dx.
5.	(x 5)(x2						7)	dx.
	(x 5)(x2						7)
7.			sinx	dx.
7.	cosx 1			dx.
	cosx 1

2.		dx	.

	1 (8x)2
	1 (8x)2

4. 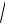x2 x 2 dx.

6. (2x 1)e4xdx.

8.	xdx	dx.


	x 1 2

2.Вычислить площадь, ограниченную кривыми y2 9x; y 3x.

3.Найти длину дуги кривой y ex ; 0 x 1.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x2 ; x 2; y 1.

123

Вариант №14

1. Вычислить неопределенные интегралы.

4x 1

dx.

5x 7e

dx.

2. 5

2 x2

(3log7 x 2)3

dx.

2x 1

dx.

x2 9x 2

7x2 1

dx.

6. (4x 8)sin8xdx.

(x2

x 1)(3x 1)

dx.

7. sin3 xcos4 xdx.

x 1

2. Вычислить площадь, ограниченную кривыми

;

y x2 6x 5.

3. Найти длину дуги кривой y

1, отсеченной прямой y 0.

4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями 2x y 2 0; x 3; y 0.

Вариант №15

1. Вычислить неопределенные интегралы.

1. (3sin x

)dx.

1 x2

6 x2

(4arctgx 3)4

dx.

1 x2

x 1

dx.

(x 8)(x 11)

7. sin3 4xcos3 4xdx.

2. 75x 11dx.

4.	x 1	dx.

	x2 6x 8
	x2 6x 8

6. (5x 8)cos3xdx.

8. x 1 1dx. x 1 5

2.Вычислить площадь, ограниченную кривыми yx 2; x y 3 0.

3.Найти длину дуги кривой y2 x 1 3, отсеченной прямой x 4.

124

ex 1

4. Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x2 5x 6;

y 0.

Вариант №16

1. Вычислить неопределенные интегралы.

8x 1

dx.

2x dx.

2. 3

4 x2

3x 1

3. 2x3

x2dx.

dx.

2x 1

6x 8

dx.

6. arcctg3xdx.

(x 1)(x2

3x 5)

7. sin5xcos5xsin10xdx.

dx.

x 1

2. Вычислить площадь, ограниченную кривыми y x2 2x; y 4 x2 .

3. Найти длину дуги кривой y lnex 1; 1 x 5.

4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями y x2; y 1; x 2.

Вариант №17

1. Вычислить неопределенные интегралы.

3cosx 7sinx 26

dx.

cos2(6x 3)

x 8

dx.

x 8

4x 6

dx.

6. arcsin8xdx.

(x 3)(x 5)

sin5 3xdx.

dx.

x 3

x 24

2. Вычислить площадь, ограниченную кривыми y (x 2)3; y 4x 8.

125

3.	Найти длину дуги кривой y 2lnsin	x	;	1	x .
				2
4.	2
	Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x2; y2 x 0.

Вариант №18

1. Вычислить неопределенные интегралы.

		x		7		8
	3 7	x	x	7		8
					3
1.					3		x	2	dx.
							x

3. xsin7x2dx.

x 8

5. (x 3)(x 3)(x 1) dx. 7. sin4 3xcos3xdx.

2. e8x 1dx.

4. x 1 dx. x2 6x 6

6. e3xx3dx.

8. 1 xdx.

1 x

2. Вычислить площадь, ограниченную кривыми y sinx cos2 x;

y 0; 0 x .

3. Найти длину дуги кривой y x2 ln x ; 2 x 4.

4.Найти объём тела, образованного вращением вокруг оси Ox облас-

ти, ограниченной линиями y x2; x 2; y 0.

Вариант №19

1. Вычислить неопределенные интегралы. 1. (2cosx 3x 4x 6x x6)dx.

exdx

3. 1 e2x .

x 8

5. (x2 5)(x 5)dx.

7. cos2xsin2 6xdx.

2. cos(12 11x)dx.

4. dx. x2 10x

6. (4x 1)23xdx.

8.	x	1	dx.


	x 1 1

126

2.Вычислить площадь, ограниченную кривыми y (x 1)2 ; y2 x 1.

3.Найти длину дуги кривой y 2lncos x;0 x .

4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями y x2 1; y x; x 0; x 1.

Вариант №20

1. Вычислить неопределенные интегралы.

	2		5	7
	2		5	7			2. cos(8x 3)dx.
					2
1.		4 x2	5 x2	7 x	2	dx.
	1	4 x2	5 x2	7 x
	1

3. x2dx.

5. (x 1)(x 6)dx.

cosx

7. sinx cosx dx.

3x 1

4. x2 10x 1dx.

6. x3 log4 xdx.

8.	3x 1dx	.


	3x 1 4

2.Вычислить площадь, ограниченную кривыми y x9 x2 ; y 0; 0 x 3

3.Найти длину дуги кривой y 1 lncos x; 0 x .

4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями y x 1; y 0; y 1; x 0,5.

Вариант №21

1. Вычислить неопределенные интегралы.

	3	6	7
1.				2	dx.

		6 x	7 x
x

3. 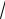5ln x 1dx. x

2.	dx	.

	4 x

4. x2 10x 2dx.

127

5.	3x2 1		dx.	6. (x3 1)lnxdx.
	(4 x)(x2	4)
						dx
7. cos4 5xdx.				8.				.

					4 x 1		x 1
2. Вычислить		площадь,		ограниченную	кривыми		y (x 3)2;

y2 x 3.

3.Найти длину дуги кривой y 10 ln x2 1 ; 2 x 5.

4.Найти объём тела, образованного вращением вокруг оси Оx облас-

ти, ограниченной линиями y x 1 2; y 1.

Вариант №22

1. Вычислить неопределенные интегралы.

	2				3		77
	2				3
1.								x dx.
1.					x2			x dx.
	x6				x2
3.		3tgx 4				dx.
3.						dx.
			cos2 x
5.					x2				dx.
5.		(x2							dx.
		(x2		10)(x 1)

7. sin5 3xdx.

2. cos2(7x 3).

x 2

4. 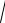x2 12x 8 dx.

6. (4x 1)cosxdx.

8. 3x 4x .

2.	Вычислить площадь, ограниченную кривыми y 2x x2 3;
y x2 4x 3.
		2	3
3.	Найти длину дуги кривой y		3 x		; 0 x 1.
				2

	3

4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями y2 x 2; y 0; y x3; y 1.

Вариант №23

1. Вычислить неопределенные интегралы

		2			1		x					dx
		2		3	1	7	x					dx
	3			3					2.		2		.
1.	3		x		x			1 dx.	2.		2	(6x 1)	.
			x		x					sin		(6x 1)

128

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.34 Mб101576.pdf
#
07.01.20211.34 Mб11577.pdf
#
07.01.20211.34 Mб161578.pdf
#
07.01.20211.34 Mб171579.pdf
#
07.01.2021317.66 Кб3158.pdf
#
07.01.20211.35 Mб221580.pdf
#
07.01.20211.35 Mб301581.pdf
#
07.01.20211.35 Mб71582.pdf
#
07.01.20211.35 Mб61583.pdf
#
07.01.20211.36 Mб21584.pdf
#
07.01.20211.36 Mб51585.pdf