
1580
.pdf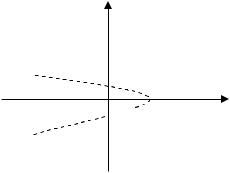
6. z x |
2 |
y |
2 |
x y; |
Д (–2; 2); |
~ |
(–2; 2; 12). |
|
|
Д |
7.2,011,02 .
8.z x2 2x 1 2y2.
9. z x2y2 |
в области x2 y2 |
1. |
|
|
||||
10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
2 |
|
3 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
y |
|
4,4 |
1,1 |
|
0,4 |
1,2 |
1,5 |
|
|
|
|
|
|
|
|
|
6.2.Пример выполнения типового расчета
1.Найти и изобразить на плоскости область определения функции
двух переменных: z |
x y |
. |
|
||
|
x y2 1 |
|
Решение. Очевидно, аналитическое выражение, задающее данную функцию, имеет смысл тогда и только тогда, когда знаменатель дроби не равен нулю: x y2 1 0. Уравнение x y2 1 0 задаёт на коор-
динатной плоскости xOy параболу y2 x 1, вершина которой находится в точке (1; 0), ветви направлены влево, а осью симметрии является ось абсцисс. Таким образом, областью определения данной функции являются все точки координатной плоскости, кроме тех, что
лежат на параболе y2 x 1.
y
О  1 x
1 x
2. Найти частные производные первого порядка функций двух переменных:
a)z ln xy.
109

Решение.
zx |
(ln xy)x |
y const |
1 |
|
(xy)x |
|
|
y |
|
|
1 |
|
; |
|
|
|
xy |
|
x |
||||||||||
|
|
|
xy |
|
|
|
|
|
|
|||||
zy |
(ln xy)y |
x const |
1 |
(xy)y |
|
|
x |
|
|
1 |
. |
|||
|
|
xy |
|
y |
||||||||||
|
|
|
xy |
|
|
|
|
|
|
|||||
б) z x4 y5.
Решение.
zx (x4 y5)x y5 (x4 ) 4x3y5; zy (x4 y5)y x4 (y5) 5x4 y4 .
в) z xtgy .
Решение.
x zx (xt g y)x tg y x tg y; zy (xtg y)x x (tg y) cos2 y .
3. Найти все частные производные второго порядка функции двух переменных: z sin xy .
Решение. Сначала найдём частные производные первого порядка:
zx (sin xy)x ycosxy; zy (sin xy)y xcosxy .
Теперь находим производные второго порядка по переменным x
и y:
zxx (ycosxy)x y2 sinxy; zyy (xcosxy)y x2 sinxy.
Находим смешанные производные:
zxy zyx ( y2 sinxy)y ( y2) sinxy ( y2) (sinxy)y
2ysinxy xy2 cosxy.
110

4. Найти производную функции z 3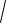 xy в точке M0 (8; 1) по направ-
xy в точке M0 (8; 1) по направ-
лению вектора l ( 1; 1).
Решение. Производная функции z f (x;y) по направлению вектора
l равна z zx cos zy cos , где cos , cos направляющие ко- |
||
l |
|
|
синусы вектора l . |
|
|
Находим частные производные данной функции: |
||
zx |
y ; zy |
x . |
|
33 (xy)2 |
33 (xy)2 |
Находим значения частных производных в точке M0 (8; 1):
zx |
|
|
1 |
; zy |
|
2 |
. |
M0 |
|
|
|||||
|
12 |
|
M0 3 |
||||
Находим направляющие косинусы вектораl |
. соs |
lx |
|
; соs |
ly |
|
; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
l |
|
|
l |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
; cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
( 1)2 ( 1)2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
( 1)2 ( 1)2 |
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||
Окончательно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
z |
|
|
1 |
1 |
|
|
|
|
2 |
|
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
7 |
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
l |
|
М0 |
12 |
2 |
|
|
|
|
3 |
|
2 |
|
|
|
12 2 3 2 |
|
|
|
|
|
|
12 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
5. Найти градиент функции z x2 |
2y2 |
xy в точкеM0 (1; 1). |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Градиент функции двух переменных z f (x; y) равен
gradz z i z j.
x y
Найдём частные производные:
zx 2x y; zy 4y x.
111

Найдём значения частных производных в точке M0 (1; 1):
|
|
zx |
M0 |
3; zy |
M0 |
5. |
|
|
||
Тогда градиент равен gradz(М) 3i 5j . |
|
|||||||||
6. Дано: функция z x |
2 |
y |
2 |
, точки Д (1; 1), |
~ |
(1; 1; 2). Требуется: |
||||
|
|
Д |
||||||||
a) линеаризовать функцию в окрестности точки Д ;
б) составить уравнение касательной плоскости и нормали к по-
~
верхности z= (x,y) в точке Д .
Решение.
a) Линеаризуем функцию z x2 y2 в окрестности точки Д, т.е. заме-
ним данную функцию линейной функцией в окрестности точки Д:
z f (x0 ; y0 ) fx (x0; y0 )(x x0 ) fy (x0; y0 )(y y0 ).
Имеем x0 1; y0 1; f (Д) f (1,1) 2.
Найдем частные производные функции в точке Д:
zx |
2x, |
zy 2y, |
zx (Д) 2 1 2, |
zy (Д) 2 1 2. |
|
x2 y2 2 2(x 1) 2(y 1) 2x 2y 2. |
|||
б) Из приближенного равенства имеем |
уравнение касательной плос- |
||||||
кости z(x; y) 2x 2y 2. |
|
|
|
|
|
|
|
Уравнение нормали имеет вид |
|
x- x0 |
|
y y0 |
|
z z0 |
. Для |
z (x0 ; y0 ) |
z (x0 ; y0 ) |
|
|||||
|
|
|
1 |
||||
заданной поверхности уравнение нормали имеет вид
x 1 y 1 z 2.
2 2 1
112
7. Найти с помощью полного дифференциала приближённое значение выражения 2,023 0,982 .
Решение. Воспользуемся приближённым равенством
f (x; y) df (x; y).
Отсюда f (x; y) f (x0 ; y0 ) df (x; y).
Рассмотрим функцию z x3 y2 . Найдём полный дифференциал этой функции:
|
dz zx x zy y 3x2 y2 x 2x3y y. |
|||
Примем x0 2; y0 |
1; |
x 0,2; |
y 0,2. Тогда получим |
|
2,023 0,982 |
23 12 |
3 22 12 0,02 2 23 1 0,02 8 0,08 7,92. |
||
Вычисление с помощью микрокалькулятора даёт результат 7,916.
8. Исследовать функцию z x2 y2 2xy на экстремумы. Решение. Областью определения данной функции является вся числовая плоскость xOy . Найдём частные производные данной функции:
zx 2x 2y; zy 2y 2x .
Производные первого порядка непрерывны на всей области определения функции. Для того чтобы найти стационарные критические точки функции, решим систему уравнений
2x 2y 0; |
x 0; |
|
|
2x 2y 0; |
y 0. |
Получили одну стационарную критическую точку M(0;0). Для того чтобы выяснить, является ли она точкой экстремума, найдём производные второго порядка.
zxx 2; zyy 2; zxy 2.
113
Найдём дискриминант: |
D AC B2 , |
где |
|||
|
|
|
(0; 0) |
|
(0; 0).. |
A zxx |
(0; 0); B zxy |
; C zyy |
|||
В данном случае A 2; B 2;C 2; D 4 4 8 0. В данной точке экстремума нет.
9. Найти наибольшее и наименьшее значения функции z xy x y в области 0 x 1;1 y 2.
Решение. Прежде всего, заметим, что данная функция непрерывна в рассматриваемой области. Найдём стационарные критические точки функции, принадлежащие указанной области. Частные производные
первого порядка zx |
y 1; zy |
x 1 |
непрерывны в данной области. |
|||||||
Составим систему уравнении |
|
|
|
|
|
|
|
|||
|
|
y 1 0; |
|
|
x 1; |
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
x 1 0; |
|
|
y 1. |
|
|
|||
Получили одну стационарную критическую точку M(1;1) . Най- |
||||||||||
дём значение функции в этой точке: |
z |
|
M 1. |
|
|
|||||
|
|
|
||||||||
Далее |
исследуем |
функцию |
на |
границе |
области: |
|||||
0 x 1;1 y 2. |
Область |
представляет |
собой прямоугольник |
|||||||
АВCD. |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
B |
C |
|
|
|
|
|
|
|
|
|
2 |
D |
|
|
|
|
|
|
|
|
|
1 A |
|
|
|
|
|
|
||
|
|
О |
1 |
|
|
|
|
|
x |
|
1)Уравнение отрезка АВ: x 0;1 y 2. Функция принимает вид z y . Функция линейная, принимающая наибольшее и наименьшее значения на концах отрезка. Тогда z y 1 1; z y 2 2.
2)Уравнение отрезка СD: x 1;1 y 2. Функция принимает вид z 1. Функция постоянная. Тогда z y 1 1, z y 2 1.
114
3) Уравнение отрезка AD: y 1; 0 x 1. Функция принимает вид
z 1. Функция постоянная. Тогда z |
|
x 0 1; z |
|
x 1 1. |
|
||||
|
|
|
|||||||
4) Отрезок ВС определяется условиями |
y 2; 0 x 1. Функция |
||||||||
принимает |
вид |
z x 2. |
Функция |
|
|
линейная. |
Тогда |
||
zx 0 2; zx 1 1.
Сравнивая все полученные величины, имеем
minz z(0; 2), max z z(1;1) z(0;1) z(1; 2).
10. Дана система точек, координаты которых указаны в таблице.
x |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
|
|
|
|
|
y |
0 |
2 |
3 |
3,5 |
3 |
4,5 |
|
|
|
|
|
|
|
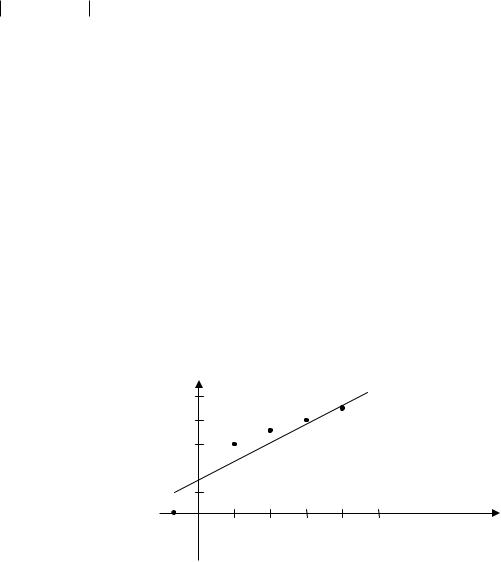
Построить по методу наименьших квадратов эмпирическую функцию y kx b для данной системы точек. Найти среднее квадратическое отклонение полученной прямой от системы точек. Решение. По заданной таблице построим точечный график функции.
y
4
3
2
1
О |
1 |
2 |
3 |
4 |
5 |
x |
По данным таблицы найдем значения параметров k и b функции приближения y kx b, для чего воспользуемся нормальной системой вида
|
n |
2 |
n |
|
x y |
; |
|
k x |
b x |
i |
|||
i 1 |
i |
i 1 |
i i |
|
||
|
|
|
i 1 |
|
||
|
n |
|
|
|
n |
|
|
|
|
|
|
||
k xi bn yi. |
|
|||||
|
i 1 |
|
i 1 |
|
||
115

Составим вспомогательную таблицу.
№ |
xi |
yi |
xi2 |
xi yi |
kxi b |
kxi b yi |
(kx b y |
i |
)2 |
п/п |
|
|
|
|
|
|
i |
|
|
1 |
-1 |
0 |
1 |
0 |
0,81 |
0,81 |
0,6561 |
|
|
2 |
0 |
2 |
0 |
0 |
1,55 |
-0,45 |
0,2025 |
|
|
3 |
1 |
3 |
1 |
3 |
2,29 |
-0,71 |
0,5041 |
|
|
4 |
2 |
3,5 |
4 |
7 |
3,03 |
-0,47 |
0,2209 |
|
|
5 |
3 |
3 |
9 |
9 |
3,77 |
0,77 |
0,5929 |
|
|
6 |
4 |
4,5 |
16 |
18 |
4,51 |
0,01 |
0,001 |
|
|
|
9 |
16 |
31 |
37 |
- |
- |
2,1766 |
|
|
Из сумм столбцов при xi , yi , xi2, xi yi составляем коэффициенты системы
31k 9b 37;
9k 6b 16.
Из решения системы находим искомые параметры : k =0,74 и b =1,55. Подставим значения найденных параметров в формулу эмпирической функции y kx b. Искомое уравнение будет иметь вид
y 0,74x 1,55.
Построим график полученной функции на том же рисунке, где изображены точки.
Сумма квадратов отклонения ординаты эмпирической функции y 0,74x 1,55 в точке xi от ординаты данной точки равна
6
2 (kxi b yi )2=2,1766.
i 1
Среднее квадратическое отклонение прямой от системы точек :
|
2 |
|
2 |
2,1766 |
|
|
|
|
|
|
|
|||
|
ср |
|
|
|
|
|
|
0,36. Среднее отклонение, которое приходится на |
||||||
6 |
6 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одну точку: ср |
|
|
|
|
2 |
|
0,6. |
|||||||
|
|
|
|
|
||||||||||
6 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
116

РАЗДЕЛ 7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
7.1. Типовой расчет
Вариант №1
1. Вычислить неопределенные интегралы. 1. 3x 7x2 cosx 1 3x2 dx.
3. 7x(4cos(7x) 1)dx.
5. |
xdx |
. |
|
||
(x 1)(x 3) |
|
|
2. 73x 5dx.
4. |
|
x 3 |
dx. |
|
|
||
x2 |
6x 1 |
||
6. (5x 8)e10xdx.
7. cos6 3xdx. |
8. |
|
|
dx |
|
|
. |
3 |
|
|
|
|
|||
|
|
x x |
|||||
2.Вычислить площадь, ограниченную кривыми y x2 ; y 2x 3.
3.Найти длину дуги кривой y x2 lnx ; 1 x 2.
42
4.Найти объём тела, образованного вращением вокруг оси Оx облас-
ти, ограниченной линиями yx 1; 1 x 5.
Вариант №2
1. Вычислить неопределенные интегралы.
|
|
|
2 |
|
3 |
|
1. |
|
2x |
|
7cosx |
|
dx. |
|
4 x2 |
|||||
|
|
|
|
|
|
3. x(3x2 10)4 dx.
x 1
5. dx. (x2 1)(x2 1)
7. sin5 xdx.
2. (7x 10)4dx.
4. |
|
3x 1 |
|
dx. |
|
|
|
||
|
x2 3x 1 |
|||
6. (7x 2)log12 xdx.
xdx
8. 
 x 2 3
x 2 3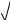 x 2.
x 2.
117

2.Вычислить площадь, ограниченную кривыми y x2 9; y 0.
3.Найти длину дуги кривой y ln x2 1 ; 2 x 3.
4.Найти объём тела, образованного вращением вокруг оси Оx облас-
ти, ограниченной линиями y2 6x; 3 x 5.
Вариант №3
1. Вычислить неопределенные интегралы.
|
|
|
|
|
|
4 |
|
x |
|||
1. |
2cosx |
3 |
|
e |
dx. |
||||||
x |
|||||||||||
|
x2dx |
|
|
|
|
|
|||||
3. |
|
|
. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
8 x3 |
|
|
|
|
|
||||||
5. |
|
|
x |
2 1 |
|
dx. |
|
|
|
||
(x2 |
|
|
|
|
|
|
|||||
|
4)x |
|
|
|
|||||||
7. sin2 xcos9 xdx.
2. |
|
|
dx |
|
. |
|
|
|
|
|
|||
|
|
|
||||
|
|
11 6x |
||||
4. |
|
|
3x 6 |
dx. |
||
|
|
|
||||
|
|
x2 x 8 |
||||
6. 3x 1 cos2xdx.
dx
8. 
 x 1 24
x 1 24 x 1.
x 1.
2.Вычислить площадь, ограниченную кривыми y x2; y 4x 3.
3.Найти длину дуги кривой y ex e x 3; 0 x 4.
2
4. Найти объём тела, образованного вращением вокруг оси Оx области, ограниченной линиями 3x y 0; 3x 4y 0; y 3.
Вариант №4
1. Вычислить неопределенные интегралы.
|
3 |
|
7 |
|
|
||
1. |
|
|
|
2x 3 dx. |
|||
|
6 x2 |
||||||
|
cos2 x |
|
|
|
|||
3. |
|
|
x2dx |
. |
|
|
|
|
33 x3 |
|
|
|
|||
|
|
x 6 |
|
|
|||
5. |
|
|
|
|
dx. |
||
|
|
|
|
|
|
||
|
|
(x 2)(x 3)(x 8) |
|||||
7. sin7 xdx.
dx
2. (33 x)3.
4. |
|
4x 1 |
|
dx. |
|
|
|
||
|
||||
|
|
x2 2x 11 |
||
6. (2x3 x)log4 xdx.
dx
8. 3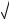 3x 1.
3x 1.
118
