Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1561

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.33 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 195 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

1, 0 x 2;

10. f x

3 x, 2 x 4.

Вариант №20

n2 7

1. а)

;

б)

;

в)

3n2

n 4

n 1 n 1 3

n 12n3

n 1

2. а)

1 ncos

; б)

1 n 4n 3;

в) 1 n n 1

3n 1

n 1

5n 1

2n 1

n 13n 2

4.f x x4 x3 2; x0 1.

5.f x 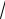1 xsin3x.

0,8 dx

6. 0 1 x3 .

7.sin . 10

8.y x x2 y2; y 0 1.

9.f x 2 x2 ; x . 12 4

4x 4 , 0 x 1;

10. f x

0,1 x 3.

Вариант №21

5n 1

3n 1!

n 1 n2

1. а)

;

б)

;

в)

n 12n 1

n 1

2. а) 1 n

; б) 1 n 1

3 ;

в) 1 n n 1

n2 1

3n 1

n 1

7n 2

n 1

3. x2 4 2n .

n 1 9n n 1

4.f x x6 ; x0 1.

5.f x ln3 1 2x .

1 x

0,3 arctgx

6. 0 x dx.

7.e 3 .

8.y y2 x; y 0 1.

9.	1, 1 x 0;
9.	f x
	x,0 x 1.

		sinx		, 0 x		;
		sinx		, 0 x		;
10.	f x				2
10.	f x				2
		0,		x 5.
		0,		x 5.
			2
			2

Вариант №22

1. а)

;

б)

;

в)

n 110n

n 1 4n 1

1 n

n 1

4n 3

n 1

1 n 1

6n 4

2. а)

;

б)

;

в) 1

n 2

3n2

n 1

n 1 lnn

n 1

x 2 n

n 1

2n 5

f x ln 3 x ;

x0 2.

f x sh3x.

dx.

cos

ln1,1.

8. y e2y ln x; y 1 1.


0, 1 x 0;
				1
				1
9. f x x,0 x					;
9. f x x,0 x					;
	1		1	3
	1	,	1	x 1.

			3
2			3
	x2			,0 x 2;
10. f x

1,2 x 4.

Вариант №23

2 n

1.а) ;

n 1 n 3 !

	2n 1	n		3
		3			.
б)		;	в)
	3n 2
n 1			n 1n 2n 1

							n 3n2			1				1 n 2			n	n 4
2. а) 1												;		б)	;	в) 1				.
2. а) 1								4n		n		;		б)	;	в) 1		3n2	3	.
			n 1					4n	2	n				n 1 n 3n		n 1		3n2	3
3.				x2n		.


	n 1n 5
4.		f x cos3x;								x0				.
4.		f x cos3x;								x0			3	.
						1							3
5.		f x				1					.
5.		f x			x2 5x 6						.
	1			dx

6.		3					.



		0 3 8 x3

7.cos . 8

8.y xy y e3y ; y 0 2,y 0 1.

3, 3 x 0;

9. f x

2x 1,0 x 3.

2 ,0 x 2;

10. f x

2 x,2 x .

Вариант №24

2n 1

1. а)

;

б)

;

в)

3n 1

n 1

n 1 2n 1!

n 1

2n7 3n2 2

2. а) 1 n

n 2

;

в) 1 nn3tg .

; б) 1

n2 13

n 14

n 1

5n3 1

n 1

x 2 4n

n 1 n 3 4n

4.f x 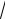3 x; x0 1.

5.f x x2cos3x.

6.	0,21 e				3x
						dx.
			x
	0
7.	3			.
		128

8.y 2x3 y2 e3y ; y 2 1.

9.f x 2 x2; x .

1 x2 ,0 x 1;

10. f x

1, 1 x .

Вариант №25

n 1

1. а)

;

б)

;

в)

n 14n 5

n 13n 1

n 1n3

6n 1

sin

n 2

3n 1

2. а) 1 n

;

б)

;

в)

n 1

n 2 n

n 1 4n 1 2n

9n 1

x2n .

4n 5

n 1

f x sin2x;

f x

1 x2

1	x5
6. ln 1		dx.
6. ln 1	5	dx.
0	5

7.ch1.

8.y cos2x siny; y .

0, 2 x 1;

9. f x 1, 1 x 1;

2, 1 x 2.

x2	,0 x 2;
10. f x	.

1,2 x 4.

11.2.Пример выполнения типового расчета

1.Исследовать сходимость знакоположительных рядов:

5n-6

а) 3n .

Решение. Исследуем ряд по признаку Даламбера. Вычисляем предел.

an 1

5 n 1 6

5n 1

lim

3n 1

lim

5n 6

n 3 5n 6

поэтому ряд является сходящимся.

б) 5n2 3.

Решение. Сравним этот ряд с обобщенным гармоническим рядом

1 (поскольку p 2 1, то он является сходящимся). n2

7n2

14n

0, .

lim

n 5n2 3

n 10n 5

При вычислении предела было использовано правило Лопиталя раскрытия неопределенностей. Предел отношения общих членов рядов не равен нулю и не равен бесконечности, поэтому теорему можно применить. Мы сравнивали со сходящимся рядом, поэтому ряд

7		тоже сходится.
5n2
	3

в) 3 . 2n 6

Решение. Исследуем ряд по интегральному признаку. Находим ООФ

функции y	3	. Получаем x 3. Теперь выбираем нижний пре-

	2x 6

a 3;

дел интегрирования a так, чтобы выполнялись условия Вари-

a 1.

антов выбора a много. Пусть, например, a 4. Теперь вычисляем несобственный интеграл:

делаем замену переменной

t 2x 6;dt 2dx;

lim

2x 6

если x 4, то t 2;

N 4 2x 6

если x N, то t 2N 6

2N 6

3dt

lim

2N 6

lim ln

2N 6

ln2

lim

N 2

2 N

Получили, что интеграл расходится. Значит, исследуемый ряд тоже расходится.

2. Исследовать сходимость знакопеременных рядов и установить характер сходимости (условная, абсолютная):

n 1 5n3			3n2 4
а) 1				.
	3n	2	2n 5

Решение. Данный ряд является знакочередующимся. Проверим, выполняются ли для него условия теоремы Лейбница:

5n3 3n2 4

lim

15n2 6n

lim

30n 6

lim

6n 2

n 3n2

2n 5

Условие не выполнено. Ряд расходится.

n	5
б) 1			.
	3
		2n 3

Решение. Проверяем условия теоремы Лейбница:

																	5			5		0 (выполнено);
											lim


											n						3 2n 3
																	5					5				(выполнено).
								3												3
								3				2 n 1 3								3	2n 3
Оба условия теоремы Лейбница выполнены, поэтому ряд сходит-
ся.																																		5
Теперь рассмотрим ряд, составленный из модулей																																		5	.
Теперь рассмотрим ряд, составленный из модулей																																	3		.
																																	3	2n 3
Этот ряд сравним отношением с обобщенным гармоническим ря-
дом	1		. Здесь p										1		1, ряд расходится. Получаем
дом			. Здесь p												1, ряд расходится. Получаем
		1						3
	n3							3
	n3
					5
			3															n										1			1
			3		2n			3										n										1			1	0; .
lim					2n			3		lim							53						lim				53			53
lim						1				lim							53	2n 3					lim				53			53
n						1					n							2n 3						n			2		2
					3
					3		n
Это означает, что ряд из модулей																									5					расходится.
																								3
																										2n 3
																	5									2n 3
												n					5
Итак,				ряд				1											является условно сходящимся (т.к. он
														3
														3		2n 3
сходится, а ряд из его модулей расходится).
						n			2n 3 5n 1
в) 1												.
в) 1												.
									3n 2

Решение. Рассмотрим ряд, составленный из модулей данного ряда

		2n 3 5n 1
			.
		3n 2

Исследуем его по радикальному признаку Коши:

2n 3 5n 1

2n 3 5

2 5

lim n

lim

3n-2

3n 2

5n 1

Ряд из модулей 2n 3 сходится, поэтому исследуемый

3n 2

n	2n 3 5n 1
ряд 1		сходится абсолютно.
	3n 2

3. Найти область сходимости степенного ряда

22n 3 x 1 n

Решение.

n 1

5n 2

Рассмотрим ряд,

составленный из абсолютных величин

данного ряда:

22n 3

x 1

. Применим к ряду из модулей признак

5n 2

Даламбера:

n 1

an 1

22 n 1 3

x 1

n 1 22n 3

x 1

5n 2

x 1.

lim

5 n 1 2

5n 2

n 5n 7

Теперь сделаем вывод о сходимости ряда:

а) если 4

x 1

1, т.е. если 1 4 x 1 1

или если

, то

по признаку Даламбера ряд сходится, причем абсолютно;

б) если 4

x 1

1 , т.е. если x

или x

, то ряд расходится;

в) если 4

x 1

1 , т.е. если x

или

, то по признаку Да-

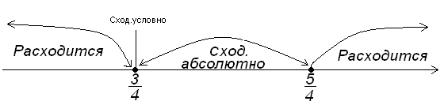
ламбера вывод о сходимости ряда сделать нельзя. Поэтому применим другие признаки.

Если x	5	, то исходный ряд имеет вид
Если x		, то исходный ряд имеет вид
4
			2n 3 5	n			1
		2		1		22n 3			2	3

							4n
			4				4n				.
			5n 2								.
	n 1		5n 2		n 1 5n 2			n 1 5n 2

Это знакоположительный ряд. Исследуем его сходимость, срав-

																						1
нив отношением с расходящимся гармоническим рядом																							:
нив отношением с расходящимся гармоническим рядом																							:
																				n 1n
			2 3		1		1		n					1		1
			2 3	:	1	lim		8	n					8		1		0	; ,
lim
lim					n
n 5n 2					n	n 5n 2								5 40
то есть признак применить можно.											Получаем, что в точке x													5	ис-
то есть признак применить можно.											Получаем, что в точке x														ис-
следуемый ряд расходится.																							4
следуемый ряд расходится.
Если x	3	, то ряд имеет вид
Если x		, то ряд имеет вид
4
			2n 3	3		n				2n 3		1	n
2					1		2											n	2	3
2					1		2
				4							4
				4							4						1				.
			5n 2							5n 2											.
n 1			5n 2				n 1			5n 2					n 1 5n 2

Это знакочередующийся ряд. Проверим для него выполнение теоремы Лейбница:

2 3

а)

lim an lim

0(выполнено);

n 5n 2

б)

2 3

(выполнено).

5 n 1 2

5n 2

Это означает, что ряд сходится. Ряд из его модулей имеет вид

2 3

. Этот ряд расходится (мы исследовали его при рассмотрении

n 15n 2

случая x

). Окончательно получаем,

что при x

степенной ряд

сходится условно.

22n 3 x 1 n

;

Итак, интервал сходимости ряда

5n 2

n 1

4. Разложить данную функцию f x

в ряд Тейлора по степе-

5 x

ням (x 2), используя формулу Тейлора.

Решение. Рядом Тейлора, разложенным по степеням

(x x0)

для

функции

f x ,

называется

степенной

ряд

вида

f x f x

f x0

x x

f x0

x x 2

f n x0

x x

Вычисляем значение функции и ее производных при x0 2:

1 2

f 2

; f 2

x 2

; f 2

; …;

5 x 2

5 x 3

x 2

f n 2

; … .

5 x n 1

x 2

3n 1

Искомый ряд имеет вид

x 2

x 2 2

x 2 n .

n 1

5 x 3 3

5. Разложить функцию f x xе x в ряд по степеням x 3, пользуясь известными разложениями элементарных функций. Указать область, в которой это разложение справедливо.

Решение. Преобразуем функцию

f x xе x x 3 3 e x 3 3 e3 x 3 e x 3 3e3e x 3 .

Теперь используем разложение в ряд функции e x , заменяя x на x 3:

<<< < Предыдущая 1 2 3 45 / 195 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.32 Mб41557.pdf
#
07.01.20211.32 Mб21558.pdf
#
07.01.20211.32 Mб41559.pdf
#
07.01.2021317.5 Кб2156.pdf
#
07.01.20211.32 Mб11560.pdf
#
07.01.20211.33 Mб711561.pdf
#
07.01.20211.33 Mб01562.pdf
#
07.01.20211.33 Mб61563.pdf
#
07.01.20211.33 Mб41564.pdf
#
07.01.20211.33 Mб01565.pdf
#
07.01.20211.33 Mб61566.pdf