Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1561

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.33 Mб

Скачать

☆

<<< < Предыдущая 12 / 192 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Вариант №17

1	y	e	1
1. dy		f( x,y)dx dy	f( x,y)dx.
0	0	1	ln y

y 20 x2; y 8x.

y2 2x x2 0; y2 4x x2 0;

; y

4. D : x 1; y 0; y2 4x ( y 0); 6x2 2y.

5. x y 4; x

; z 0.

2y; z

Вариант №18

f( x,y)dx

f( x,y)dx.

2 y2

18 x2

; y 3

18 x2

y2 2y x2 0; y2 14y x2 0;

;

y x.

4. D : x2 y2 9; x2 y2 16; y 0; x 0( x 0; y 0);																	2y 5x	.
4. D : x2 y2 9; x2 y2 16; y 0; x 0( x 0; y 0);																		.
																	x2 y2
5. x 5					; x 5y		; z 0; z				5	(3			).
				y
														y
														y
			6		18				18
								Вариант №19
			0				2		0
1.		3	0				2		0
1.	dx				f( x,y)dy dx					f( x,y)dy.
2.	0		4 x2		2			3		4 x2
2.	y sin x;				y cosx;	x 0( x 0).
3.	y2 10x x2 0; y2 14x x2 0; y												x			; x 0.

	1		3
4. D : x		; y 0; y2 8x ( y 0);	7x 2y2.

3

5. x 192y; x 42y; z 0; z y 2.

Вариант №20

1.	1	0		0				0
1.	dy			f( x,y)dx dy				f( x,y)dx.
	2	y 2			1			3	y

2.	y		24 x2		; x2 2		y; x 0( x 0).
2.	y		24 x2		; x2 2	3	y; x 0( x 0).
3.	y2 4y x2 0; y2 8y x2 0;									y	x	; y		x.
											x		3
													3
										3

4. D : x2 y2 4; x2 y2 16; y 0; x 0( x 0; y 0);
	2y 3x			.
				.
	x2 y2
5. y		5			5	x; z 0; z		5	(3		).
		5	x; y		5			5		x
			x; y							x
3			9				9
							Вариант №21
1 y						e	0

1. dy f( x,y)dx dy f( x,y)dx.

	0	0						1					ln y
	y		3				; y			3	; x 9.
2.			3		x					3
2.
		2								2x											x
3.	y2 10x x2 0; y2 6x x2 0;																	y		2		; y					x.
																				2						3
																			2							3
						1													2
4. D : x						1	; y 0; y2 8x ( y 0); 7x 2y2.
4. D : x							; y 0; y2 8x ( y 0); 7x 2y2.
		3
5. x2 y2 2; x
5. x2 y2 2; x												y; x 0; z 0; z 30y.
																Вариант №22
			sin x												cos x
1.	4		sin x									2			cos x
1.		dx						f( x,y)dy dx								f( x,y)dy.
	0	0													0
												4
2.	y			12 x2					; y 3							12 x2	; x 0( x 0).
2.	y			12 x2					; y 3					2		12 x2	; x 0( x 0).
																		y x; y						x	.
3.	y2 6y x2 0; y2 12y x2 0;																						2	x
3.	y2 6y x2 0; y2 12y x2 0;
																			2

4. D : x 3; y 0; y2 6x ( y 0); x 3y2.

5.	y 17								1	.
				2x; y 2			2x; z 0; x z		1
				2x; y 2			2x; z 0; x z
								3
								Вариант №23
1.	1	x2	2					2 x
1.	dx		f( x,y)dy dx					f( x,y)dy.
	0	0	1					0
2. x2 y2 12;						y x2 ( y 0).
2. x2 y2 12;					6	y x2 ( y 0).
3.	y2 14x x2 0; y2 4x x2 0; y x; y											x.
3.	y2 14x x2 0; y2 4x x2 0; y x; y										3	x.

4. D : x2 y2 4; x2 y2 36; y 0; x 0( x 0; y 0);																														2y x	.
4. D : x2 y2 4; x2 y2 36; y 0; x 0( x 0; y 0);																															.
														12x																x2 y2
5. x y 2; x																		; z 0.
												y; z
												y; z
												5
																	Вариант №24
				2
									4 x2						2					4 x2
1.		3							4 x2						2					4 x2
1.	dx									f( x,y)dy					dx					f( x,y)dy.
	0				0											3			0
2. x 5 y2; x 4y.																								x
3.	y2 20y x2 0; y2 40y x2 0; y																								; y				x.
																												3
																												3
																						3
4. D : x 7; y 0; y2 4x ( y 0); 3x 6y2.
5. x 20																						1	.
								2y; x 5					2y; z 0; z y									1
								2y; x 5					2y; z 0; z y									2
																						2
																	Вариант №25
																			2
						4 x2									0						4 x2
1.			3			4 x2									0						4 x2
1.		dx								f( x,y)dy					dx						f( x,y)dy.
	2				0												3		0
							; y				1	; x 16.
2.	y				x						1
2.	y			2							2x
				2							2x
3.	y2 24x x2 0; y2 40x x2 0;																					y x; y				3	x.

4. D : x2 y2 25; x2 y2 36; y 0; x 0( x 0; y 0); 7y x . x2 y2

5. x	5			5y	; z 0; z	12x	.
			y; x

2		6			5

9.2. Пример выполнения типового расчета

2 x

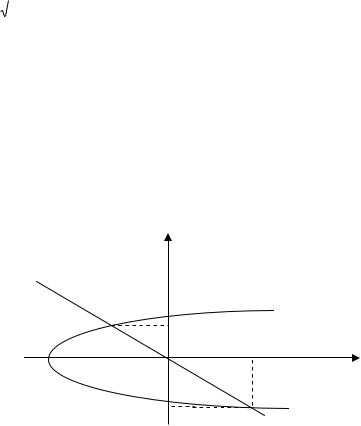
1. Изменить порядок интегрирования dx f( x,y)dy. Область интег-

0 x2

рирования изобразить на чертеже.

Решение. Область интегрирования D правильная в направлении оси

Оy :

1 x 1
D	2		.
x		y 2 x

x y

D1 x=2-y

Для смены порядка интегрирования проецируем область D на ось Оy и получаем отрезок 0,2 . Фиксируем y (0,2).Замечаем, что область D является сложной в направлении оси Оx, так как точки выхода из области D лежат на линиях, которые задаются различными уравнениями: для 0 y 1 линией выхода является парабола x y , для 1 y 2 – прямая x 2 y. Следовательно, область D необходимо разбить на две области (D D1 D2) прямой y 1.

0 y 1			1 y 2
D1		; D2		.

0 x	y		0 x 2 y

Используя свойство аддитивности двойного интеграла по области интегрирования, имеем

					1	2 x
f (x, y)dxdy f (x, y)dxdy f (x, y)dxdy dx						f (x,y)dy=
D			D1	D2	0	x2
				2 y
1		y	2	2 y
= dy			f (x,y)dx dy f (x, y)dx.
0	0		1	0

2. Найти площадь фигуры D, ограниченной данными линиями: y2 4 x;3y x 0.

Решение. Построим область D.

	y
x 3 y	x y2 4
	x y2 4
	1
-4	12
D	x
	-4

Площадь области вычисляем по формуле SD dxdy.

Область интегрирования D – сложная в направлении оси Оy и простая в направлении оси Оx. Поэтому для вычисления двойного интеграла переходим к вычислению повторного, у которого внутреннее интегрирование по переменной х, внешнее – по переменной y.

				4 y 1
			D						.
				y2 4 x 3y
Переходим к вычислению повторного интеграла:
	1	3y	1		3y				1		2		5

SD dxdy= dy		dx		x	y	2	4	dy	3y	y		4dy 20		(кв.ед.)

D	4	y2 4	4						4				6

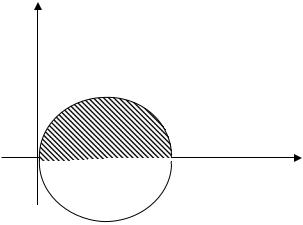
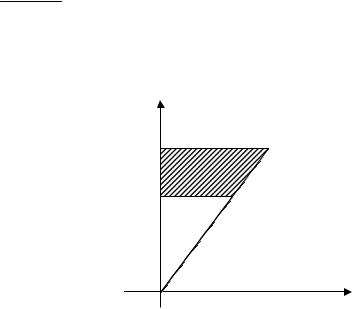
3.Найти площадь фигуры, ограниченной линиями x2 y2 2x;

x0( y 0).

Решение. Построим область D. Запишем уравнение границы области x2 y2 2x в виде (x 1)2 y2 1. Уравнение определяет в декартовой системе координат окружность с центром в точке С (1,0) и радиусом R=1. Область интегрирования D представляет собой верхнюю часть круга.

y
		2
		2

r 2cos

Определим уравнения границ области D в полярной системе координат. Область D – правильная в полярной системе координат.

	x rcos ;	то полярное уравнение окружности
Так как		то полярное уравнение окружности
	y rsin ,

x2 y2	2x примет вид r 2cos . Тогда D 0				. Площадь
x2 y2	2x примет вид r 2cos . Тогда D 0			2	. Площадь

		0	r 2cos

области вычисляем по формуле SD dxdy. Переходим к полярным

координатам:		ydxdy= rdrd .
		D	D
	Вычисляем интеграл:
		2cos		r	2

	2		2			2cos 2	2	2	1 cos2 d
rdrd = d rdr d							cos2	d
rdrd = d rdr d							cos2	d
В	0	0	0	2		0	0	0
В	0	0	0	2			0	0

sin2
	2		(кв. ед.).


2	0	2

4. Вычислить массу материальной пластины плотностью

y3
(x,y) x2 y2 ,	если	она	ограничена	линиями

y 2; y 4; x 0; x y.

Решение. Построим область D.

4 y=2

y=x

y=1

0 1

Массу пластины вычисляем по формуле


mD (x, y)dxdy			y3	dxdy.
mD (x, y)dxdy		2	y2	dxdy.
D	D x	2	y2

2 y 4 D 0 x y .

Перейдем к вычислению повторного интеграла для определения

3 y

массы: m

dxdy=

D x

0 x

2 0 x

4	2		x	y	4 y2				3	4	16

y		arctg		0			dy	y		0		.

0			y		0	4	12				3

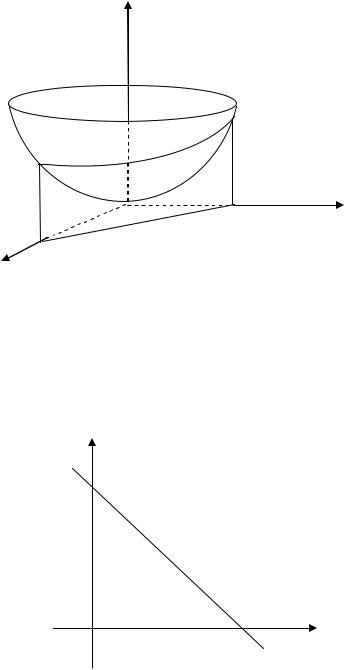
5. Вычислить объем тела, ограниченного поверхностями z x2 y2; x y 4; x 0; y 0; z 0.

Решение. Построим области V, ограниченной поверхностями. Уравнение z x2 y2определяет параболоид вращения, x y 4 – плоскость, параллельную оси Оz и отсекающую на осях Оx и Оy от-

z x2 y2

x y 4

резки, равные 4. Уравнение x 0 определяет координатную плоскость ОYZ, уравнение y 0 – координатную плоскость ОХZ, уравнение z 0 – координатную плоскость Оxy. Имеем цилиндроид, ограниченный сверху поверхностью z f (x, y) x2 y2.

Построим отдельно область D.

y=4-x

x=0

y=0

Объем построенного тела вычисляем по формуле

	V			f( x,y)dxdy x2 y2dxdy.
			D					D
Перейдем к вычислению кратного интеграла. Область D есть тре-
угольник, ограниченный в плоскости ОХY										прямой x y 4						и коор-
динатными осями x 0 и				y 0. Область D является простой в обоих
			0 x 4
направлениях. Тогда D						.
			0 y 4 y											1
		2		2		4	4 x		2		2	4	2			3	4 x
		2		2		4	4 x		2		2	4	2			3	4 x
V f (x, y)dxdy x			y		dxdy= dx			( x		y		)dy x		y	x		0
V f (x, y)dxdy x			y		dxdy= dx			( x		y		)dy x		y	x		0
D	D					0	0					0		3
D	D					0	0					0		3

4	2		1		3		2	(куб.ед).
x		(4 x)		(4 x)		dx 42
x		(4 x)		(4 x)		dx 42	3
0			3				3

РАЗДЕЛ 10. ЭЛЕМЕНТЫ ВЕКТОРНОГО ПОЛЯ

10.1 Типовой расчет

Дано векторное поле а P(x,y,z)i Q(x, y,z) j R(x, y,z)kи уравнения поверхностей 1 и 2, ограничивающих замкнутую поверхность .

Требуется:

1)сделать схематический чертеж поверхности 1 2;

2)найти дивергенцию векторного поля а;

3)проверить, является ли поле соленоидальным;

4) найти поток поля а через замкнутую поверхность 1 2 с помощью формулы Гаусса-Остроградского;

5)дать заключение о наличии источников или стоков внутри области, ограниченной поверхностью ;

6) вычислить циркуляцию векторного поля по контуру Г, образованному пересечением поверхностей 1 и 2(направление обхода должно быть выбрано так, чтобы область, ограниченная контуром Г, находилась слева);

7)вычислить ротор векторного поля a;

8)проверить правильность вычисленной циркуляции с помощью формулы Стокса.

Вариант №1

а (2x z)i (2y xz) j (4 2x)k; 1 : x2 y2 2z 3 0; 2 : z 2.

Вариант №2

а (x 2)i (y xz) j (3 z)k; 1 : x2 y2 2z 1 0; 2 : z 1.

Вариант №3

а (2x z)i (2y xz) j (3 x)k;

1 : x2 y2 2z 3 0; 2 : z 1.

<<< < Предыдущая 12 / 192 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.32 Mб41557.pdf
#
07.01.20211.32 Mб21558.pdf
#
07.01.20211.32 Mб41559.pdf
#
07.01.2021317.5 Кб2156.pdf
#
07.01.20211.32 Mб11560.pdf
#
07.01.20211.33 Mб711561.pdf
#
07.01.20211.33 Mб01562.pdf
#
07.01.20211.33 Mб61563.pdf
#
07.01.20211.33 Mб41564.pdf
#
07.01.20211.33 Mб01565.pdf
#
07.01.20211.33 Mб61566.pdf