Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1561

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.33 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 193 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Вариант №4

а (x 6)i (xz y) j (1 z2 )k; 1 : x2 y2 2z 5 0; 2 : z 2.

Вариант №5


а 3zi (4 xz)j (z2 3x)k;	1 : x2 y2 2z 7 0; 2 : z 3.
Вариант №6
а (x z)i (y xz) j (2z x)k;		1 : x2 y2 2z 0; 2 : z 2.
Вариант №7
а 2xi (xz 2y) j (4 z2 )k;	1 : x2 y2 2z 3 0; 2 : z 1.
Вариант №8
а (2x z)i (xz 2y) j (x z)k;		1 : x2 y2 2z 1 0; 2 : z 1.
Вариант №9
а (3x z)i (3y xz) j (1 x)k;		1 : x2 y2 2z 3 0; 2 : z `2.
Вариант №10
а (x 1)i (y 2 xz)j zk;	1 : x2 y2 2z 5 0; 2 :z 3.

Вариант №11

а (3y 5x)i (6x 5y) j (4x xy 4)k; 1 :x2 y2 2z 3 0; 2 :z 2.

Вариант №12

а (x y)i (2x y) j (x2 2z 4)k; 1 : x2 y2 2z 1 0; 2 : z 1.

Вариант №13

а (3x 2y)i (5x 2y) j (3z y2 3)k; 1 : x2 y2 2z 3 0; 2 : z 1.

Вариант №14

а (3x 4y)i (3y x) j (xy 2z 4)k; 1 : x2 y2 2z 5 0; 2 : z 2.

Вариант №15

а ( x 2y)i (x 2y) j (3z 2xy 9)k; 1 : x2 y2 2z 7 0; 2 :z 3.

Вариант №16

а (7x 5y)i (8x y) j (3xy 2z 2)k; 1 : x2 y2 2z 0; 2 : z 2.

Вариант №17

а (2x 3y)i (5z 4y) j (6z 2y2 6)k; 1 :x2 y2 2z 3 0; 2 : z 1.

Вариант №18

а (6x 5z)i (3x y) j (2y2 z 4)k; 1 : x2 y2 2z 1 0; 2 : z 1.

Вариант №19

а (y 2x)i (4x 3y) j (3z 2y2 9)k; 1 : x2 y2 2z 3 0; 2 : z 2.

Вариант №20

а (5x 4y)i (7x 2y) j (2xy z 4)k; 1 : x2 y2 2z 5 0; 2 : z 3.

Вариант №21

а (x y)i (2x y)j (x2 2z 4)k;

1 : x2 y2 2z 1 0; 2 : z 2.

Вариант №22

а (x 2)i (y xz) j (3 2z)k; 1 : x2 y2 2z 1 0; 2 : z 1.

Вариант №23

а (x z)i (2y xz) j (3 xy)k; 1 : x2 y2 2z 3 0; 2 : z 1.

Вариант №24

а (x 6)i (xy z) j (1 y2 )k; 1 : x2 y2 2z 5 0; 2 : z 2.

Вариант №25

а zi (4 2xz)j (z2 3x)k; 1 : x2 y2 2z 7 0; 2 : z 3.

10.2 Пример выполнения типового расчета

Дано векторное поле а (3y 5x)i (6x 5y) j (4z xy 4)k и уравнения поверхностей , 1 : x2 y2 (z 1)2; 2 : z 1, ограничивающих замкнутую поверхность .

Решение.

1) В данном задании замкнутая поверхность ограничена ча-

стью плоскости 2 : z 1 и частью конуса 1 : x2 y2 (z 1)2 (z 1). Поверхность проецируется взаимно-однозначно на плоскость Оxy в область D – круг с центром в точке О(0,0) и радиусом R=2.

2	z	n			k
2	1	n	2		k
	1		2
1	O				2	y
	O				2	y
x				Sxy
	-1

2) Дивергенцию находим по формуле

diva P Q R.x y z

В нашем задании

P(x, y) 3y 5x, Q(x, y) 6x 5y,Q(x, y) 4z xy 4.

Тогда

diva (3y 5x)x (6x 5y)y (4z xy 4)z 5 5 4 4.

3) Векторное поле является соленоидальным, если в каждой точ-

ке его дивергенция равна нулю. В нашем случае diva 4 0. Следовательно, данное поле не является соленоидальным.

4) По формуле Остроградского-Гаусса искомый поток векторного поля через замкнутую поверхность равен

		П	divadv.
			V
Имеем div		4, тогда П	4 dV .
Имеем div	a	4, тогда П	4 dV .
			V

Для вычисления тройного интеграла перейдем к цилиндрическим координатам по формулам

x rcos ;

y rsin ;.

z z.

Найдем уравнение верхней части конуса 1 : x2 y2 (z 1)2 в цилиндрических координатах.

(rcos )2 (rsin )2 (z 1)2 z r 1.

Установим пределы интегрирования в кратном интеграле по области V.

Имеем

		0 2
	V D 0 r 2 .

	r 1 z 1
Найдем искомый поток
П	diva dV =4 d rdr dz 32							.
		2	2			1
	V	0	0			r 1	3
5) Так как найденный в данном задании поток векторного поля
через замкнутую	поверхность		П			0,	то	векторное поле
а (3y 5x)i (6x 5y) j (4z xy 4)					содержит источники внутри
а (3y 5x)i (6x 5y) j (4z xy 4)				k	содержит источники внутри

области, ограниченной поверхностью 1 2 .

6) Контур L задается как пересечение поверхностей, т.е.

x2 y2 (z 1)2 ;

z 1.

Циркуляция векторного поля a по контуру L вычисляется по формулеЦ adl. В нашем случае имеем

Ц adl=(3y 5x)dx (6x 5y)dy (4z xy 4)dz.

L	L
Конyром L	является окружность x2 y2 4, полученная в ре-

зультате сечения конуса 1 : x2 y2 (z 1)2			плоскостью 2 : z 1. Па-
			x 2cost;
				Отсюда
раметрические уравнения этой линии имеют вид y 2sint ;				Отсюда

			z 1.
находим dx 2sintdt;	dy 2costdt;	dz 0.

Направление обхода контура выбирается так, чтобы ограниченная им область оставалась слева. Следовательно, обход окружности

x2 y2 4 будем совершать против часовой стрелки, если смотреть с конца оси Оz.

Найдем искомую циркуляцию, переходя к определенному интегралу:

Ц adl=

(3y 5x)dx (6x 5y)dy (4z xy 4)dz

x2 y2 4

((6sint 10cost)( 2sint) 2(12cost 10sint)cost)dt 12 .

7) Найдем ротор векторного поля

а (3y 5x)i (6x 5y) j (4z xy 4)

rota

P Q R

3y 5x

6x 5y

4z xy 4

(4x xy 4z)

(6x 5y)

(4z xy 4)

(3y 5x)

(6x 5y)

(3y 5x)

k x i y j 3k .

8) Согласно формуле Стокса, циркуляция векторного поля по контуру L равна потоку ротора этого поля через поверхность , натя-

нутую на контур L.Ц adl= rota nd .В качестве поверхности ,

L
натянутой на контур L	x2 y2 (z 1)2 ;
натянутой на контур L	:	,возьмем часть плоскости
	z 1,
2 : z 1, ограниченную окружностью		x2 y2	4, т.е. круг радиусом

R=2. Тогда единичный вектор нормали к плоскости 2 : z 1 будет n2 k и скалярное произведение

rota n rota k 0( x) 0 y 1 3 3.

Следовательно,

Ц			2	2
Ц	adl= rota nd 3 d 3	dxdy 3		d rdr 12 .
L		x2 y2 4	0	0

Получили тот же результат, что и в пункте 6).

РАЗДЕЛ 11. РЯДЫ

11.1.Типовой расчет

1.Исследовать сходимость знакоположительных рядов.

2.Исследовать сходимость знакопеременных рядов и установить характер сходимости (условная, абсолютная).

3.Найти область сходимости степенного ряда.

4.	Разложить данную функцию	f x в ряд Тейлора по степеням
x x0 , используя формулу Тейлора.
5.	Разложить данную функцию	f x в ряд Маклорена, пользуясь

известными разложениями элементарных функций. Указать области,

вкоторых эти разложения справедливы.

6.Вычислить значение определенного интеграла с точностью до

0,0001.

7.Вычислить значение функции с точностью до 0,001.

8.Методом последовательного дифференцирования найти первые 4−5 членов разложения в ряд решения дифференциального уравнения.

9. Разложить данную функцию f x в ряд Фурье в указанном интервале. Построить график функции и график суммы ряда Фурье.

10. Разложить функцию f x , заданную на интервале 0 , l , в ряд Фурье по косинусам (четные варианты), по синусам (нечетные варианты). Построить график функции и график суммы ряда Фурье.

Вариант №1

2n 1

3n 1

1. а)

;

б)

;

в)

n 1

2 n2

n 13n 5

n 1n

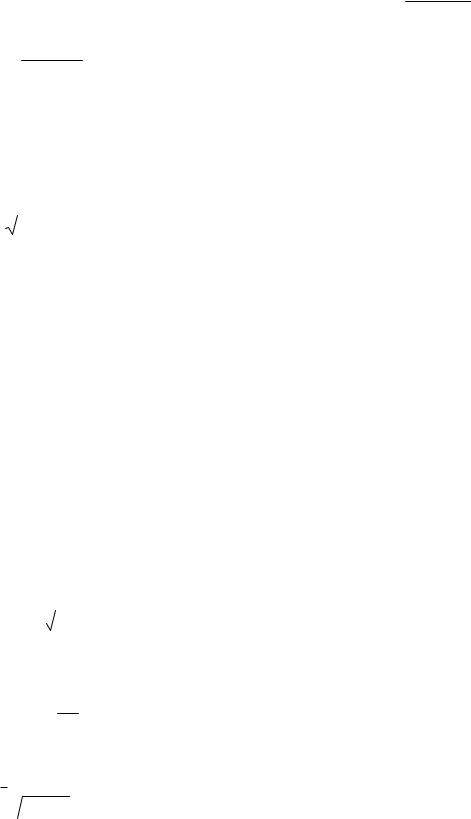
1 n 1 3n 2		1 n
2. а)		; б)	;
	6n 5
n 1		n 17n 1

x 3 n

3. .

n 1 n 4n

1 n n2

в) .

n 1 n 1!

4.f x x4 5x2 5; x0 2.

5.f x 2 x e x.

	2		x2
6.			7 dx.
	e
	0
7.	3		.
		7		y
8.	y x2				4;	y 1 1.

9. f x =x2 x; 1 x 1.

cos2x,0 x			;
cos2x,0 x			;
	2
10. f x	2
0,		x .
0,		x .
	2
	2

Вариант №2

1. а) 5 3n 2 ;

б) 1

;

2n 1

в) 2n 3

n 1

2n 4

n 1

3n 2

1 n

n 3n 4

2. а)

;

б)

; в) 1

n 15

2n 3

n 15n 3n 2

n 1

n 2

3. x 1 n 6n 4.

n 1

5n 3

4. f x x3 ; x0 2.

5. f x xln 1 x2 .

6. 31 x3dx.

7.cos .

8.y sinx y3; y 0 1.

9.	0, 2 x 0;
	f x
	2x,0 x 2.
		2
				x ,0 x		;

10.	f x		2

		1,			x .

			2

Вариант №3

	5n 2 2n 5		1
1. а)		; б)		;
	7n 11

n 1		n 14 4n2 1

n ln2n

1 n 2 n3

2. а) 1

;

б)

;

3n 1

n 1

x 2 n 1n!

n 1

400

f x 2x ; x0 0.

f x

1 x 2x2

cos

dx.

ln 1,3.

y 2 1.

y lnx xy2;

0, 2 x 1;

f x

x 2, 1 x 1;

1, 1 x 2.

0 ,0 x 2;

10. f x

1,2 x 5.

3n 2 в) n .

n 1 2

sinn
в)		.
	n5
n 1

Вариант №4

2n 1!

n 5

1. а)

; б)

;

в)

n 1

n 16n 2

n 1

n3 3

n 3n 1

1 n

1 n 1 7n

2. а) 1

;

б)

; в)

n 1

n 2n 1

n 1 n 1 n 2 n

n 1

3. 3n 2 x3n 1 .

n 15n2 1

4.		f x	1		; x	0	1.
4.		f x	3 x 2		; x		1.
			3 x 2
5.	f x x 2 sin4x.
		1
	4
6.		ln 1		x dx.
	0
7.		e 3.					y 1 0.
8.		y e3y x2 4y;					y 1 0.
9.		f x	x, x 0;
9.		f x
			2x, 0 x .

2 ,0 x 3;

10. f x

3 x,3 x 4.

Вариант №5

2n 3

2n 1

1. а)

;

б)

;

в)

n n 1

n 1

n 15n 2

n 5n

1 n 1n3

1 n n 2

2. а)

; б)

;

в)

n 1!

n 1

n 1 4n

n 1

n 2

x 3

n 1 2n 3 5n

4.f x x4 3x 1; x0 1.

5.f x x 1 sin x .

<<< < Предыдущая 1 23 / 193 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.32 Mб41557.pdf
#
07.01.20211.32 Mб21558.pdf
#
07.01.20211.32 Mб41559.pdf
#
07.01.2021317.5 Кб2156.pdf
#
07.01.20211.32 Mб11560.pdf
#
07.01.20211.33 Mб711561.pdf
#
07.01.20211.33 Mб01562.pdf
#
07.01.20211.33 Mб61563.pdf
#
07.01.20211.33 Mб41564.pdf
#
07.01.20211.33 Mб01565.pdf
#
07.01.20211.33 Mб61566.pdf