
Физика_лек_pdf / Модуль 6. Магнитостатика. Магнитное поле
.pdf
возрастании магнитного поля В е сверхпроводники I и II рода будут вести себя поразному. Если внешнее приложенное поле В е достигает критического значения В к , то в случае сверхпроводников I рода сверхпроводящая фаза становится термодинамически неустойчивой и весь образец переходит в более устойчивую — нормальную — фазу. Дробление сверхпроводника на малые сверхпроводящие и нормальные домены не наблюдается, так как на образование границ между ними требуется дополнительная затрата энергии. В соответствии с этим на диаграмме состояния сверхпроводника I рода существуют только две области: сверхпроводящая и нормальная (рис. 182). Не то будет в случае сверхпроводников II рода. Так как здесь поверхностная энергия отрицательна, то имеется возможность понижения полной свободной энергии системы путем дробления образца на сверхпроводящие и нормальные домены. Такое дробление не связано с формой образца, а является внутренним свойством сверхпроводников II рода. Кроме того, в отличие от промежуточного состояния, где доменная структура сравнительно грубая и видна невооруженным глазом, домены в сверхпроводниках II рода значительно мельче (порядка 10– 5 см и меньше). Описанное состояние сверхпроводника II рода, в котором он существует в виде сверхпроводящих и нормальных доменов, называется смешанным состоянием. На диаграмме состояния сверхпроводника II рода (рис. 184) различают три области: сверхпроводящую, область смешанного состояния и нормальную область.
Границы между этими областями определяют «нижнее» B к1 и «верхнее» В к2 критические поля. Сверхпроводники II рода (сверхпроводящие сплавы) нашли применения в качестве соленоидов, предназначенных для получения сильных магнитных полей (около 100 кГс). Сверхпроводники I рода для этой цели не годятся из-за низких значений критических магнитных полей, разрушающих сверхпроводимость.
Рис. 184
10. Физическая природа сверхпроводимости была понята только в 1957 г. Еще задолго до этого Ландау была создана теория сверхтекучести гелия II . Оказалось, что сверхтекучесть — это макроскопический квантовый эффект. Однако перенести теорию Ландау на явление сверхпроводимости мешало то обстоятельство, что атомы гелия, обладая нулевым спином, подчиняются статистике Бозе (1894–1974) — Эйнштейна. Электроны же, обладая половинным спином, подчиняются принципу Паули и статистике Ферми-Дирака . Для таких частиц невозможна бозе-эйнштейновская конденсация,
необходимая для возникновения сверхтекучести. Решающий шаг в понимании сверхпроводимости был сделан американскими физиками Бардином (р. 1908), Купером (р. 1930) и Шриффером (р. 1931). Их теория в математическом отношении была усовершенствована советским физиком Н.Н. Боголюбовым (р. 1909). Основная идея заключается в следующем.

Между электронами металла существует кулоновское отталкивание. Однако оно в значительной степени ослаблено экранирующим действием положительных ионов решетки. Между тем взаимодействие электронов с колебаниями решетки приводит к слабому притяжению между ними. Это притяжение есть квантовый эффект. Оно при определенных условиях может превзойти кулоновское отталкивание между электронами, и тогда электроны группируются в пары (куперовские пары ). Эти пары, обладая нулевым спином, ведут себя как бозе-частицы и переносят электрический ток в сверхпроводниках. Ограничимся этим замечанием, так как здесь невозможно входить в теорию сверхпроводимости по существу.
Цит. по: Общий курс физики. Учеб. пособие для вузов.
В5 т. Т. III. Электричество. / Сивухин Д.В. / — 4-е изд., стереот.
—М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2004. — С. 317–327.
Тема 2. Уравнения максвелла
Ток смещения
1. Основные уравнения электромагнитного поля в неподвижных средах, применимые не только к постоянным, но и к переменным электромагнитным полям, были установлены Максвеллом. К уравнениям Максвелла можно прийти путем последовательного обобщения опытных фактов. Надо решить, какие из полученных ранее уравнений могут быть сохранены, какие должны быть отброшены и какие надо обобщить. Есть один руководящий принцип, который позволяет продвинуться в этом направлении. Следует исключить из числа основных такие уравнения, в основе которых лежит представление о непосредственном действии на расстоянии. К ним относятся законы Кулона, Био и Савара и пр. Эти законы несовместимы с экспериментально подтвержденным представлением о конечной скорости распространения взаимодействий, а потому не могут оставаться верными во всех случаях. Можно сохранить только такие уравнения, которые не противоречат представлениям теории поля. Так мы и поступали во всем предшествовавшем изложении. Мы выдвинули в качестве гипотезы, что теорема
Гаусса , уравнение  и закон электромагнитной индукции являются общими законами электродинамики. То обстоятельство, что они удовлетворяют требованиям теории поля, следует из того, что их можно представить в дифференциальной форме divD
и закон электромагнитной индукции являются общими законами электродинамики. То обстоятельство, что они удовлетворяют требованиям теории поля, следует из того, что их можно представить в дифференциальной форме divD
= 4πρ, divB = 0 и  К основным уравнениям электродинамики мы присоединим и закон сохранения электрического заряда. В дифференциальной форме он имеет вид
К основным уравнениям электродинамики мы присоединим и закон сохранения электрического заряда. В дифференциальной форме он имеет вид
(81.1)
Если электромагнитное поле стационарно, то это уравнение переходит в
divj = 0. (81.2)
2. Теорема о циркуляции

(81.3)
также может быть преобразована в дифференциальную форму:
(81.4)
а потому удовлетворяет требованиям теории поля. Однако она не может входить в число основных уравнений электродинамики. Действительно, дивергенция всякого ротора тождественно равна нулю. Поэтому, взяв дивергенцию от обеих частей уравнения (81.4), получим divj = = 0. Но это соотношение справедливо только для стационарных токов. В общем случае оно противоречит уравнению (81.1). Сомневаться в справедливости уравнения (81.1) нет оснований, так как оно выражает закон сохранения электрического заряда. Отсюда следует, что уравнения (81.3) и (81.4) могут быть верны только для стационарных токов. Для переменных электромагнитных полей они должны быть обобщены. Чтобы прийти к обобщенным уравнениям, воспользуемся следующим наводящим рассуждением. Поскольку дивергенция левой части уравнения (81.4) тождественно равна нулю, в правой части этого уравнения должен стоять вектор, дивергенция которого также всегда равна нулю. В случае стационарных электромагнитных полей этот вектор должен переходить в j . Легко указать вектор, удовлетворяющий этим условиям. Дифференцируя по времени соотношение divD = 4πρ, получаем
или ввиду уравнения (81.1)
(81.5)
Величину
(81.6)
Максвелл назвал током (точнее, плотностью тока) смещения, а сумму j + j см —
полным током. Таким образом,
div ( j + j см ) = 0, (81.7)
т.е. полный ток всегда соленоидален. Поэтому противоречие с уравнением (81.1) устранится, если в уравнении (81.4) ток проводимости j заменить полным током, т.е. написать
(81.8)

Так и поступил Максвелл.
Приведенные рассуждения ни в какой мере не могут служить доказательством уравнения (81.8). На них следует смотреть только как на один из бесконечного множества способов устранения математического противоречия между уравнениями (81.1) и (81.4). А что таких способов бесконечно много, видно уже из того, что не возникает новых математических противоречий, если в правой части уравнения (81.8) добавить произвольный вектор, дивергенция которого равна нулю. Настоящим доказательством уравнения (81.8) могут служить только опытные факты, подтверждающие это уравнение.
3. К необходимости обобщения уравнений (81.3) и (81.4) можно прийти также с помощью других соображений. Приведем два примера.
Пример 1. Пусть в неограниченную однородную среду помещен металлический шар, которому сообщен электрический заряд Q (рис. 188). Если среда проводящая, то появятся электрические токи, текущие в радиальных направлениях. Они будут возбуждать магнитное поле. При попытке указать его направление возникает следующая трудность. Вектор В не может иметь радиальной составляющей. Система сферически симметрична. Если бы радиальная составляющая вектора В существовала, то она была бы одной и той же во всех точках всякой сферы S , концентрической с поверхностью шара. Радиальная составляющая В на сфере S была бы всюду направлена либо от центра, либо к центру шара. В обоих случаях поток вектора В через сферу S был бы отличен от нуля, что
противоречит уравнению  . Следовательно, вектор В должен быть перпендикулярен к радиусу, проведенному из центра шара к рассматриваемой точке. А это также невозможно, так как все направления, перпендикулярные к радиусу, ничем не выделены — все они совершенно равноправны. Единственная возможность, допускаемая симметрией шара, состоит в том, что векторы В и Н всюду должны равняться нулю. Но в таком случае должен равняться нулю и ток j , как это непосредственно следует из уравнения (81.4). Значит, уравнение (81.4) и эквивалентное ему уравнение (81.3) в рассматриваемом случае не могут быть верными.
. Следовательно, вектор В должен быть перпендикулярен к радиусу, проведенному из центра шара к рассматриваемой точке. А это также невозможно, так как все направления, перпендикулярные к радиусу, ничем не выделены — все они совершенно равноправны. Единственная возможность, допускаемая симметрией шара, состоит в том, что векторы В и Н всюду должны равняться нулю. Но в таком случае должен равняться нулю и ток j , как это непосредственно следует из уравнения (81.4). Значит, уравнение (81.4) и эквивалентное ему уравнение (81.3) в рассматриваемом случае не могут быть верными.
Рис. 188
Для устранения возникшего противоречия необходимо допустить, что магнитные поля возбуждаются не только токами проводимости, а еще чем-то. К току проводимости I надо что-то добавить, чтобы уничтожить возбуждаемое им магнитное поле. Эта добавка и есть ток смещения. Его значение I см определится из условия I + I см = 0. Полный ток проводимости, текущий от заряженного шара, связан с зарядом Q соотношением I = – dQ / dt , а потому I см = dQ / dt . По закону Кулона Q = r 2 D . Дифференцируя это выражение и разделив результат на поверхность сферы 4π r 2 , найдем плотность тока смещения:

Это выражение совпадает с (81.6).
4. Пример 2. Соединим проводом обкладки плоского заряженного конденсатора (рис. 189). По проводу потечет электрический ток. Допущение, что в этом случае применима формула (81.3), снова приводит к трудностям. Циркуляция вектора Н , стоящего в левой части уравнения (81.3), зависит только от формы и расположения контура L . Она — величина вполне определенная. Между тем ток I , стоящий в правой части того же уравнения, таким свойством не обладает. Для определения I надо мысленно натянуть на контур L какую-то поверхность S и найти пронизывающий ее ток. Однако сила переменного тока может меняться вдоль провода. В этих случаях величина I будет зависеть от того, в каком месте поверхность S пересекается с проводом. С особой отчетливостью указанная неопределенность проявится, если поверхность S провести между обкладками конденсатора, нигде не пересекая провода. Тогда I = 0. Для устранения неопределенности к току I в уравнении (81.3) надо добавить какое-то слагаемое I см , чтобы сумма I + I см не зависела от выбора вспомогательной поверхности S . Это слагаемое и есть ток смещения.
Рис. 189
Независимость полного тока I + I см от формы натянутой на один и тот же контур L , эквивалентна утверждению, что полный ток через любую замкнутую поверхность всегда равен нулю. Токи, удовлетворяющие этому условию, не совсем удачно называются замкнутыми. Замкнутость токов не следует понимать в смысле замкнутости линий тока. Если линии тока замкнуты, то и сами токи также замкнуты. Обратное справедливо не всегда: линии тока в случае замкнутых токов не обязательно должны быть сами замкнутыми. Таким образом, формальное содержание гипотезы Максвелла сводится к утверждению, что полные токи всегда замкнуты. Токи проводимости, если они не замкнуты, замыкаются токами смещения.
Из условия замкнутости полного тока можно получить и выражения для тока смещения и его плотности. Обратимся снова к примеру с конденсатором. Идеализируя систему, можно сказать, что по проводу течет только ток проводимости, а через конденсатор — только ток смещения. Ток смещения дополняет ток проводимости до замкнутого тока. Поэтому ток проводимости в проводе должен быть равен току смещения в конденсаторе: I см = Q , где Q — заряд на той пластине конденсатора, к которой течет ток. Очевидно, Q = S ζ = SD /(4 π ). Дифференцируя по времени и разделив на S , снова получаем

Таким образом, тремя различными способами мы приходим к одному и тому же выражению для плотности тока смещения.
5.Токи смещения существуют только там, где меняется электрическое поле (точнее, электрическое смещение D ). Поэтому физическое содержание гипотезы Максвелла о токах смещения сводится к утверждению, что переменные электрические поля являются источниками магнитных полей. Это открытие принадлежит всецело Максвеллу. Оно вполне аналогично открытию электромагнитной индукции, согласно которому переменные магнитные поля возбуждают поля электрические.
6.Ток смещения в диэлектрике состоит из двух существенно различных слагаемых. По определению вектора электрической индукции D = Е + 4πР , а потому
|
(81.9) |
Величина |
называется плотностью тока поляризации. Вектор поляризации |
определяется выражением  Суммирование ведется по всем связанным зарядам, находящимся в единице объема вещества. Дифференцируя это выражение по времени, получим
Суммирование ведется по всем связанным зарядам, находящимся в единице объема вещества. Дифференцируя это выражение по времени, получим
где v i — скорость движения г-го заряда. Таким образом, ток поляризации есть электрический ток, обусловленный движением связанных зарядов. Последние принципиально ничем не отличаются от свободных зарядов. Поэтому нет ничего неожиданного в том, что токи поляризации возбуждают магнитное поле. Принципиально
новое содержится в утверждении, что и вторая часть тока смещения  которая не связана ни с каким движением зарядов, а обусловлена только изменениями электрического поля по времени, также является источником магнитного поля. Даже в вакууме всякое изменение электрического поля во времени возбуждает в окружающем пространстве магнитное поле. Открытие этого обстоятельства — наиболее существенный и решающий шаг, сделанный Максвеллом при построении своей электродинамики.
которая не связана ни с каким движением зарядов, а обусловлена только изменениями электрического поля по времени, также является источником магнитного поля. Даже в вакууме всякое изменение электрического поля во времени возбуждает в окружающем пространстве магнитное поле. Открытие этого обстоятельства — наиболее существенный и решающий шаг, сделанный Максвеллом при построении своей электродинамики.
Система уравнений Максвелла
1. Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл смог написать систему фундаментальных уравнений электродинамики. Таких уравнений четыре. В интегральной форме они имеют вид
(82.1)
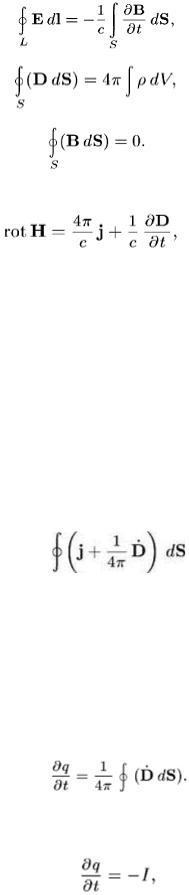
(82.2)
(82.3)
(82.4)
В дифференциальной форме:
(82.1а )
 (82.2а ) divD = 4πρ, (82.3а )
(82.2а ) divD = 4πρ, (82.3а )
divB = 0 (82.4 a )
В число фундаментальных не включено уравнение непрерывности, выражающее закон сохранения электрического заряда, так как это уравнение является следствием уравнений (82.1) и (82.3). Действительно, возьмем бесконечно малый контур L , натянем на него произвольную конечную поверхность S , а затем стянем этот контур в точку,
оставляя поверхность S конечной. В пределе циркуляция  Н dl обратится в нуль, S превратится в замкнутую поверхность, а уравнение (82.1) перейдет в
Н dl обратится в нуль, S превратится в замкнутую поверхность, а уравнение (82.1) перейдет в
Интеграл  ( j dS ) есть ток I , вытекающий из объема V , ограниченного поверхностью S . Кроме того, записав уравнение (82.3) в виде
( j dS ) есть ток I , вытекающий из объема V , ограниченного поверхностью S . Кроме того, записав уравнение (82.3) в виде
 ( D d S ) = 4 πq
( D d S ) = 4 πq
и дифференцируя его по времени, получим
В результате получится уравнение
выражающее закон сохранения электрического заряда. Тот же закон можно получить из дифференциальных уравнений (82.1а ) и (82.3а ). Достаточно взять дивергенцию от обеих

частей уравнения (82.2а ) и воспользоваться уравнением (82.3а ). Тогда получится уравнение (81.1).
Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но, насколько известно в настоящее время, нет зарядов магнитных. Стремление достигнуть симметрии уравнений электродинамики заставило Дирака выдвинуть гипотезу о существовании магнитных зарядов — единичных магнитных полюсов , или монополей. Логических возражений против такой гипотезы нет. Если бы она оправдалась, то потребовалось бы обобщение уравнений Максвелла. К источникам магнитного поля добавились бы магнитные заряды, а к источникам электрического поля — магнитные токи, обусловленные движением таких зарядов. Справедливость же самих уравнений Максвелла была бы ограничена теми областями пространства, в которых нет магнитных зарядов и магнитных токов. Однако многочисленные попытки экспериментально обнаружить магнитные монополи не привели к положительному результату.
2. Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Можно, однако, достигнуть полной математической эквивалентности обеих форм уравнений Максвелла. Для этого надо дифференциальные уравнения дополнить граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Эти условия содержатся в интегральной форме уравнений Максвелла. Они были выведены в соответствующих местах курса и имеют вид
D 2n – D 1n = 4πζ, (82.5)
B 1n = B 2n , (82.6)
E 1 t = E 2 t , (82.7)
(82.8)
Здесь ζ — поверхностная плотность электрических зарядов, a i — поверхностная плотность тока проводимости на рассматриваемой границе раздела. В частном случае, когда поверхностных токов нет, последнее условие переходит в
H 1 t = H 2 t , (82.9)
Подчеркнем еще раз, что рассуждения, с помощью которых мы пришли к уравнениям Максвелла, ни в коей мере не могут служить их доказательством. Существенно новые принципы никогда не содержатся в старой теории и не могут быть выведены из нее логически. В этом смысле нельзя вывести и уравнения Максвелла. На них следует смотреть как на основные аксиомы электродинамики, полученные путем обобщения опытных фактов.
3. Фундаментальные уравнения Максвелла в форме (82.1)–(82.4) или (82.1а )–(82.4а ) не составляют еще полной системы уравнений электромагнитного поля. Среди них два уравнения векторных и два скалярных. Если их записать в координатной форме, то получится всего восемь уравнений, связывающих 16 величин: пятнадцать составляющих векторов Е , D , В , Н , j и скаляр ρ. Ясно, что для 16 величин восьми уравнений недостаточно. Фундаментальные уравнения Максвелла не содержат никаких постоянных, характеризующих свойства среды, в которой возбуждено электромагнитное поле. Необходимо дополнить эти уравнения такими соотношениями, в которые входили бы величины, характеризующие индивидуальные свойства среды. Эти соотношения называются материальными уравнениями.
Принципиальный способ получения материальных уравнений дают молекулярные теории поляризации, намагничивания и электрической проводимости среды. В основе таких теорий лежат какие-то идеализированные модели среды. Применяя к ним уравнения классической или квантовой механики, а также методы статистической физики, можно установить связь между векторами Р , I , j , с одной стороны, и векторами Е и В — с другой. Таким путем, в зависимости от характера среды и электромагнитного поля, получаются более или менее сложные соотношения, которые и дополняют фундаментальные уравнения Максвелла до полной системы уравнений электродинамики.
Наиболее просты материальные уравнения в случае слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных неферромагнитных и несегнетоэлектрических сред материальные уравнения могут быть записаны в виде
D = ε Е , (82.10) В = μ Н , (82.11) j = λ Е , (82.12)
где ε , μ , λ — постоянные, характеризующие электромагнитные свойства среды. Они называются диэлектрической и магнитной проницаемостью и электрической проводимостью среды. Такими материальными уравнениями пользовался сам Максвелл. Разумеется, он не связывал величины ε , μ , λ c атомными и молекулярными константами вещества, а рассматривал их как постоянные, вводимые в теорию феноменологически. Электронная теория показала, что справедливость таких материальных уравнений связана с выполнением двух условий. Во-первых, за времена порядка собственных периодов внутриатомных и внутримолекулярных колебаний электромагнитное поле должно меняться мало. Во-вторых, поле должно меняться мало на протяжении межатомных и межмолекулярных расстояний. Это и есть та «медленность» изменения полей, о которой говорилось выше.
Иногда уравнения (82.10)–(82.12) также включают в систему уравнений Максвелла. Мы не будем этого делать, так как эти уравнения не обладают той общностью и фундаментальностью, которая свойственна уравнениям Максвелла. Под уравнениями Максвелла мы будем понимать только четыре уравнения: (82.1)–(82.4) или (82.1а )–(82.4а ).
Когда поля стационарны (∂ D /∂ t = ∂ B /∂ t = 0), уравнения Максвелла распадаются на две группы независимых уравнений. Первую группу составляют уравнения электростатики

rotE = 0, divD = 4 πρ , (82.13)
вторую — уравнения магнитостатики
(82.14)
В этом случае электрическое и магнитное поля независимы друг от друга. Источниками электрического поля будут только электрические заряды, источниками магнитного поля
— только токи проводимости.
Скорость распространения электромагнитных возмущений
1. Из уравнений максвелловской электродинамики следует существование принципиально нового физического явления, предсказанного самим Максвеллом. Это — электромагнитные волны, или возмущения, распространяющиеся в пространстве с определенной скоростью. Убедимся в этом на простейшем примере. Рассмотрим бесконечно протяженную однородную диэлектрическую среду с диэлектрической и магнитной проницаемостями ε и μ . Поместим в нее бесконечную равномерно заряженную плоскость, которую примем за координатную плоскость XY (рис. 190). Пока плоскость вместе с зарядами на ней неподвижна, электрическое поле в окружающем пространстве будет нормально к плоскости и равно Е = 2πζ/ε, как это следует из теоремы Гаусса и соображений симметрии (ζ — поверхностная плотность заряда, ). Приведем теперь плоскость вместе с зарядами на ней в движение в направлении оси X с произвольно меняющейся скоростью. Тогда, как будет показано ниже, появится магнитное поле и поперечная составляющая электрического поля, т.е. составляющая, параллельная заряженной плоскости. Это — переменные поля, которые и будут интересовать нас в настоящем параграфе. Что касается нормальной составляющей вектора Е , то она останется без изменений, так как рассуждения, с помощью которых была получена формула E = 2 πζ , сохраняют силу и в рассматриваемом случае, если только величину Е заменить на Dn . Нормальная составляющая вектора Е есть просто статическое электрическое поле заряженной плоскости, накладывающееся на переменное электромагнитное поле движущихся зарядов. Так как статическое поле нас не интересует, то можно совсем не обращать внимания на наличие нормальной составляющей поля Е , что мы и будем делать. Можно было бы совсем избавиться от нормальной составляющей, поместив бесконечно близко от заряженной плоскости вторую такую же неподвижную плоскость, заряженную противоположно. Электрическое поле такой плоскости было бы чисто статическим и уничтожило бы нормальную составляющую, о которой мы говорили. В то же время новая заряженная плоскость, поскольку заряды на ней неподвижны, не оказала бы никакого влияния на переменное поле электромагнитной волны.
