Физика_лек_pdf / Модуль 7. Физика колебаний и волн

ФИЗИКА КОЛЕБАНИЙ И ВОЛН

Тема 1. Механические колебания

Гармонические колебания. Дифференциальное уравнение собственных гармонических колебаний материальной точки

Движения и циклические процессы, характеризуемые определенной повторяемостью во времени, называют колебаниями. Они чрезвычайно распространены в природе и технике. Это суточные и годичные изменения температуры, морские приливы и отливы, волны на поверхности морей и океанов, разрушительные колебания коры планеты, биение сердца, дыхательный ритм, вибрации механизмов и сооружений (амплитуда колебаний вершины Останкинской телебашни при сильном ветре достигает 2,5 м), движение поршней двигателей внутреннего сгорания, акустические процессы, тепловое движение ионов и атомов кристаллической решетки твердого тела и движение электронов в атоме, переменный ток и его электромагнитное поле. В ряде случаев колебания играют отрицательную роль. Это колебания (вибрации) крыльев самолета; моста, возникающие из-за толчков на стыках рельс, при прохождении поезда; корпуса корабля, вызванные вращением гребного винта и т. п. Все эти процессы могут привести к катастрофическим последствиям. В подобных случаях необходимо воспрепятствовать тому, чтобы колебания достигли опасных размеров. Вместе с тем колебательные процессы составляют основу некоторых технических устройств и даже отраслей техники. Так, радиотехника основана на колебательных процессах.

В зависимости от характера воздействия, вызывающего и поддерживающего колебательный процесс, колебания классифицируют на свободные (или собственные), вынужденные, автоколебания и параметрические.

Свободные или собственные колебания происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок или она была выведена из положения равновесия. Примером собственных колебаний является движение подвешенного на нити шарика.

Вынужденные колебания появляются в системе от воздействия внешней периодически изменяющейся силы. Примером вынужденных колебаний может служить колебание моста, возникающее при прохождении по нему шагающих в ногу людей.

Автоколебания, как и вынужденные колебания, сопровождаются воздействием на систему внешних сил, но при этом система сама управляет внешним воздействием. Примером автоколебательной системы являются часы. В них маятник получает толчки за счет энергии поднятой гири или упругой пружины. Однако толчки происходят в те моменты времени, когда маятник проходит через среднее положение.

Параметрические колебания в системе происходят также от внешнего воздействия при периодическом изменении одного из параметров системы. Примером параметрических колебаний является движение шарика, подвешенного на нити переменной длины.

Физическая природа колебаний может быть разной, и поэтому колебательные системы принято классифицировать на механические, электрические, информационные, биологические и др. Особое значение имеют колебания двух видов: механические и

электромагнитные. К механическим относят колебания маятников, струн, вибрации различных механизмов и сооружений, а также акустические колебания, волны на поверхности водоемов и др. К электромагнитным — колебания тока в электрической цепи, колебания напряженности электрического и магнитного полей в электромагнитной волне. По форме колебания могут быть разделены на прямоугольные, треугольные и синусоидальные (рис. 13.1).

Опыт указывает на многообразие форм колебательного движения и на то, что анализ их осуществляется единым методом. Простейшими являются гармонические колебания, при которых колеблющаяся величина изменяется со временем по закону косинуса — синуса. Большая часть реальных колебаний близка к гармоническим, и в ряде случаев подобные колебания идеализируются и считаются гармоническими. Важным является и то обстоятельство, что периодические процессы иной негармонической формы могут быть представлены как наложение нескольких гармонических колебаний. Теория гармонических колебаний используется буквально во всех разделах физики: в теории упругости, акустике, оптике, электричестве и электромагнетизме, учении об атоме и др.

Рис. 13.1

Одним из методов графического изображения гармонического колебания является метод вращающегося вектора амплитуды {рис. 13.2), называемый также методом векторных диаграмм. Для этого из точки О , взятой на оси х, под углом θ откладывается

вектор 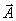, модуль которого равен амплитуде A рассматриваемого колебания. Пусть вектор

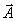движется против часовой стрелки с угловой скоростью ω = const . Проекция конца вектора на ось х или s будет перемещаться вдоль оси и принимать значения от +А до –А. Отклонение колеблющейся величины х со временем определяется соотношением x = A cos θ , а применительно к оси s – s = A sin θ . На этом же рисунке дано графическое построение синусоиды. Итак, гармоническое колебание может быть представлено

проекцией вектора амплитуды на произвольно выбранную ось. Именно такое изображение гармонического колебательного процесса воспроизводится регистрирующими приборами.

Рис. 13.2

Рассмотрим основные кинематические параметры гармонических колебаний.

1.Отклонение (смещение s = f ( t )) — мгновенное вертикальное перемещение относительно положения равновесия, м.

2.Амплитуда А — максимальное отклонение (смещение), м. Большинство реальных колебательных процессов не являются строго периодическими. И в связи с этим изменение амплитуды позволяет выделить незатухающие, затухающие, нарастающие и амплитудно-модулированные колебания (рис. 13.3). Последний тип колебательного движения, в котором амплитуда периодически изменяется, называется биениями.

Рис. 13.3

3.Периодичность, то есть повторяемость движения по истечении времени Т, называемая периодом колебания. Это минимальный промежуток времени, через который происходит повторение процесса. Итак, период Т = 1 / v , с, есть длительность полного колебания, то есть промежуток времени, в течение которого фаза колебания получает приращение 2 π рад.

4.Число колебаний к моменту времени t равно п = t / T . Количество повторений процесса п в течение времени t называют частотой, в данном случае колебательного

процесса, v = n / t , с–1 . Следовательно, частота колебаний v = 1 / Т , с–1 = Гц, представляет собой число колебаний в единицу времени. В качестве единицы измерения частоты в СИ используется герц. 1 Гц соответствует одному колебанию в секунду.

5.Угловая, круговая или циклическая частота, называемая прежде угловой скоростью, ω = Δθ / t . Так как ωТ = 2π, то ω = 2π / Т = 2 πv , рад/с. Заметим, что Т = – 2π

/ω. Циклическая частота равна величине изменения фазы в единицу времени, то есть скорости изменения фазы.

6.Фаза θ = ωt + θ0 = 2 πt / T + θ 0 = 2 πvt + θ0 , рад — термин греческого происхождения и в переводе на русский язык означает «проявление». В физике это следует понимать как конкретную в фиксированный момент времени стадию развития периодического процесса. Например: начало его, максимум развития, минимум и т. д. Однако изложенного определения фазы, как физической величины, недостаточно. Физический смысл фазы состоит в том, что она определяет смещение в любой момент времени и, следовательно, состояние колебательной системы. Фазам, различающимся между собой на величину, кратную 2π рад, соответствуют одинаковые смещения. Отметим еще раз, что изменение фазы на 2π рад соответствует отрезку времени в один период Т. И еще один нюанс из области воспоминаний. Пересчет радиан в градусы осуществляется следующим образом: θ° = θрад · 57,3°.

7.Начальная фаза θ0 , рад — значение фазы в момент начала колебаний при t = 0. При определении фазы необходимо учитывать начальную фазу θ 0 — рис. 13.4.

Рис. 13.4

8. Время t — отсчитывается от момента начала колебаний.

Из уравнения 13.2 следует дифференциальное уравнение гармонических колебаний

Решением этого уравнения является s = A cos (( ωt + θ0 ).

Энергия гармонического колебания

Энергия системы, колеблющейся без затухания, постоянна. Она складывается из кинетической Е к и потенциальной Е п составляющих. Значения обеих компонент энергии меняются периодически, но в каждый момент времени Е = Е к + Е п . Рассмотрим гармоническое колебание материальной точки массой m вдоль оси х относительно начала координат, как центра равновесия (рис. 13.6).

Рис. 13.6

Рассмотрим кинетическую составляющую энергии колебательного движения. Согласно общей формуле Е к = 0,5 mv 2 и формуле (13.1) имеем Е к = 0,5 mA 2 ω 2 sin 2 ( ωt + θ0 ). Поскольку sin2 α = 0,5(1 – cos2α), то окончательно получим

Рассмотрим потенциальную составляющую энергии материальной точки, колеблющейся под действием силы F = та. Колебательное движение рассматриваемой системы является гармоническим и описывается, , дифференциальным уравнением (13.3) d 2 x / dt 2 = – ω 2 x = ак , м/с2 . С учетом изложенного

Поскольку cos 2 α = 0,5(1 + cos 2 α ), то окончательно получим

Знак «минус» означает противоположный характер изменения Е п и вектора ускорения.

Сложив (13.4) и (13.5), получим формулу для энергии (полной) гармонического колебания

Итак, энергия гармонически колеблющейся материальной точки, как уже отмечалось, постоянна и пропорциональна квадрату амплитуды колебаний А 2 . В колебательном процессе происходит непрерывный переход кинетической энергии в потенциальную и обратно. Однако сумма их в любом из состояний точки остается постоянной. Когда же точка проходит через положение равновесия х = 0, потенциальная компонента обращается в нуль, а кинетическая — достигает максимума и равна при этом полной энергии. Когда же колеблющаяся точка доходит до одного из крайних положений х = ± А, то v = 0 и Е к = 0, а Е п = max и равна полной энергии гармонического колебания.

Гармонический и ангармонический осциллятор

Систему, колебания которой совершаются относительно устойчивого центра равновесия, называют осциллятором. Если колебания системы являются гармоническими, то такую систему называют гармоническим осциллятором. В теории колебаний гармонический осциллятор представляет собой модель, широко используемую в ряде задач классической и квантовой физики. Реальным примером гармонического осциллятора могут быть пружинный, математический и физический маятники, электрический колебательный контур.

Пружинный маятник — это двухкомпонентная система, состоящая из груза массой т и абсолютно упругой пружины (рис. 13.7).

Рис. 13.7

Подобная система способна к гармоническим колебаниям вдоль оси х под действием упругой силы Fx = – kx , где k — коэффициент упругости, кг/с2 . В данном случае его называют еще жесткостью. Именно упругая сила пружины используется в качестве возвращающей силы системы. По второму закону Ньютона: та = — k х. Тогда уравнением движения пружинного маятника следует считать

Из уравнения движения очевидно, что циклическая частота пружинного осциллятора равна

а его период

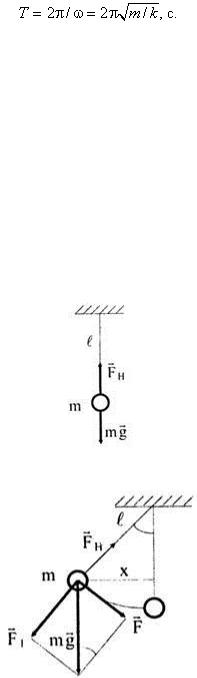
Если учесть, что в формуле E п = 0,5 mA 2 ω 2 cos 2 ( ωt + θ ), A 2 cos 2 ( ωt + θ ) = x 2 , a ω 2 = k / m , то потенциальная энергия пружинного маятника при действии на него упругой силы пропорциональна квадрату отклонения груза от положения равновесия и определяется соотношением Е п = k х 2 / 2. Этот же результат известен из раздела «Механика».

Пружинный маятник является примером свободного механического осциллятора, колеблющегося без энергетических потерь. Антиподом его могут рассматриваться гравитационные маятники, к которым относятся математический и физический маятники.

Математический маятник — это идеализированная система, состоящая из материальной точки массой т и невесомой не деформируемой нити длиной l (рис. 13.8,

13.9).

Рис. 13.8

Рис. 13.9

В состоянии равновесия системы силы тяжести и натяжения F н уравновешивают друг друга (рис. 13.8).

Если вывести маятник из положения равновесия, то движение материальной точки будет совершаться под действием возвращающей силы тяжести mg (рис.13.9), которая в этом случае будет направлена под углом к силе натяжения F н . При движении маятника эти силы не могут быть уравновешены. Из рис. 13.9 очевидно, что значение возвращающей силы составляет часть силы тяжести mg и определяется величиной угла отклонения α : F = mg sinα . Опытом установлено, что математический маятник совершает гармонические колебания, если угол отклонения не превышает 8°. При этом условии можно допустить sinα α = х / l (рис. 13.9). Учитывая противоположность направлений смещения материальной точки и возвращающей силы, получаем F = – rngx / l , где х — значение смещения маятника от положения равновесия. Ускорение маятника равно:

а циклическая частота —

Период колебаний математического маятника при α ≤ 8° 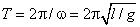, с, не зависит от массы маятника и амплитуды его колебаний.

Практическое значение математического маятника состоит в том, что, используя его, можно определить ускорение g силы тяжести.

Физический маятник — это твердое тело с распределенной массой, совершающее гармонические колебания под действием силы тяжести вокруг неподвижной горизонтальной оси А подвеса, не совпадающей с центром масс О (рис. 13.10) маятника. Программа не предусматривает рассмотрение параметров колебания физического маятника. Кстати, африканские женщины с грузом на голове подобны физическому маятнику. Масса груза может достигать 20 % от массы его носительницы. Считают, что КПД этого способа переноса тяжестей выше других. Объясняют это колебательным движением груза.

Рис. 13.10

Наряду с гармоническим осциллятором существует понятие ангармонического (нелинейного) осциллятора. Его колебания, конечно же, отличаются от гармонических. И основная особенность их состоит в том, что частота и период колебаний ангармонического осциллятора зависят от амплитуды. Нелинейность осциллятора может быть продемонстрирована, например, одномерным движением материальной точки в потенциальном поле. И оказывается, что траектория точки имеет форму несимметричной потенциальной ямы. Анализ нелинейного осциллятора требует предварительного рассмотрения уравнения движения одномерного гармонического осциллятора. Этот вопрос достаточно объемен и сложен, не говоря уже о самом ангармоническом осцилляторе. Вопрос о нем можно рассматривать как специальный. По этой причине нелинейный осциллятор в настоящем учебном пособии не описывается.

Сложение гармонических колебаний одного направления смещения и одинаковой частоты

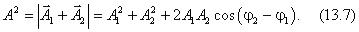
На практике чаще приходится встречаться со сложными колебаниями. Их можно рассматривать как результат сложения гармонических колебаний. Если материальная точка участвует одновременно в двух колебаниях, то величина смещения точки в каждом из колебаний равна:

х1 = A 1 cos(ωt + θ 1 ), м ,

х2 = A 2 cos(ωt + θ 2 ), м .

Частоты обоих колебаний равны, и совершаются они вдоль одного направления смещения, а амплитуды А 1 и А 2 и начальные фазы колебаний θ1 и θ2 различны. Так как векторы А 1 и А 2 вращаются с одинаковой угловой скоростью (циклической частотой ω), то разность фаз (θ2 – θ1 ) между ними остается постоянной. Результирующее смещение материальной точки, одновременно участвующей в двух колебаниях, определяется алгебраическим сложением смещений точки в каждом из колебаний

х = х 1 + х 2 = A cos ( ωt + θ), м.

Так как смещения х 1 и х 2 через период времени T возвращаются к своим первоначальным значениям, то их сумма x представляет собой периодическое колебание с тем же периодом T . Такое колебательное движение можно иллюстрировать графически,

используя метод вращающихся векторов и (рис. 13.11). При вращении обоих векторов против часовой стрелки с постоянной угловой скоростью ω = const их проекции х 1 и х 2 на ось О x будут совершать гармонические колебания. Причем в силу равенства

угловых скоростей векторов 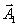и 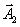угол между ними θ2 – θ1 = const . Построим по

правилу параллелограмма вектор 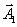(рис. 13.11). Из рисунка очевидно, что проекция х этого вектора на горизонтальную ось равна алгебраической сумме проекций исходных

векторов х 1 + х 2 = х. Изменение проекции вектора , равномерно вращающегося с угловой скоростью ω , будет происходить по гармоническому закону с периодом Т = 2π / ω, с. По модулю результирующая амплитуда гармонического колебания по теореме косинусов равна: