Физика_лек_pdf / Модуль 10. Квантовая физика

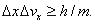
содержания. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда следует практическая невозможность одновременного измерения с одинаковой степенью точности координаты и импульса микрочастицы. Причем это не связано с техническими трудностями измерения. Никакой эксперимент не может дать большей точности в определении этих величин, чем та, которая следует из принципа Гейзенберга.

Соотношение неопределенностей Гейзенберга допускается записывать в виде

Из этого соотношения очевидно, что степень неопределенности координаты и скорости микрообъекта обратно пропорциональна его массе. Это значит, что чем больше масса частицы, тем меньше неопределенность ее координаты и скорости и, следовательно, с тем большей точностью можно применить к такой частице понятие траектории. Примеры этому рассмотрим ниже.

В квантовой теории, помимо соотношения неопределенностей между координатой и импульсом (или скоростью), рассматривается также важное соотношение неопределенностей для энергии и времени. Можно доказать, что если частица некоторое время t находится в нестационарном состоянии, то энергия этого состояния не может

Здесь E — неопределенность в величине энергии частицы, a t — время жизни частицы в том состоянии, в котором определяется эта энергия. Таким образом, при среднем времени жизни t микросистема не может быть охарактеризована определенным значением энергии. Разброс энергии Е ≥ h t возрастает с уменьшением t .

Соотношение неопределенностей в свое время явилось темой философских дискуссий. Некоторые из физиков утверждали, что соотношение неопределенностей указывает границу познания природы, ограниченность наших познавательных способностей. В действительности, принцип Гейзенберга имеет объективное содержание и не связан с отрицанием познания. Подлинный смысл принципа состоит в своеобразном выражении качественно новой природы микрочастиц, которые объективно не имеют точных координат и импульсов и движение которых объективно является бестраекторным. Другими словами, отсутствие возможности одновременно точно измерить координату и импульс, например, электрона в атоме обусловлено не тем, что этому что-то мешает, а тем, что этих классических понятий координаты, скорости и импульса у электрона просто нет. Таким образом, принцип неопределенности является следствием объективно существующей двойственности свойств микрочастиц и свидетельствует об объективно существующих ограничениях в возможности описания поведения микрообъектов с помощью классических понятий координаты, скорости и импульса. Именно отказ от строгой определенности, присущей классической механике, труднее всего-то и воспринимается образным представлением изучающих этот раздел физики.

Волновая функция и ее статистический смысл

Итак, принцип Гейзенберга ограничивает применение классической механики к микрообъектам, которые, помимо дискретных, обладают еще и волновыми свойствами.

Открытие волновых свойств у движущихся микрочастиц вещества послужило фундаментом для создания квантовой механики — раздела теоретической физики, изучающего законы движения микрообъектов с линейными размерами 10– l 0 – 10–15 м, а также их взаимодействие между собой и структурными элементами вещества. Квантовая механика, изучающая движение микрочастиц со скоростями v << с , называется нерелятивистской, а при v ≤ с — релятивистской квантовой механикой. Рождение ее относится к 1900 г., когда М. Планк сформулировал квантовую гипотезу. Выдающаяся роль в развитии квантовой механики принадлежит трудам В. Гейзенберга, Э. Шредингера

иП. Дирака.

Вквантовой механике принципиальный интерес представляет физическая природа волн де Бройля. Чтобы разобраться в этом, следует сравнить дифракцию световых волн и микрочастиц.

Отдельная волна, падающая на дифракционную решетку, порождает множество вторичных волн, усиливающих или ослабляющих друг друга. Дифракционная картина от световых волн, как известно, характеризуется тем, что вследствие наложения дифрагирующих волн в различных точках пространства происходит усиление или ослабление амплитуды колебаний- А интенсивность дифракционной картины согласно волновым представлениям о природе света пропорциональна квадрату амплитуд световых волн. Если же рассматривать дифракцию света с позиции его дискретных свойств, то интенсивность света в конкретной точке дифракционной картины определяется числом фотонов, попадающих в эту точку. Таким образом, число фотонов в конкретной точке дифракционной картины задается квадратом амплитуды световой волны. Квадрат же амплитуды определяет вероятность попадания одного фотона в конкретную точку.

Дифракционная картина, например, от электронов в результате их рассеяния и отражения также характеризуется неодинаковым распределением потока микрочастиц по различным направлениям. Каждый электрон за решеткой летит в определенном направлении. При этом оказывается, что вероятность его движения в том или ином направлении изменяется так же, как и интенсивность волн де Бройля за решеткой. Это значит, что большую интенсивность волн следует ожидать там, где будет большее число электронов. Таким образом, следует вывод о том, что интенсивность волн де Бройля в конкретной точке определяет число электронов в этой точке. Следовательно, дифракционная картина от электронов есть проявление статистической, вероятностной закономерности попадания микрочастиц в те места, где интенсивность волн де Бройля наибольшая.

Именно необходимость вероятностного подхода к изучению микрочастиц является важнейшим положением квантовой теории. Однако следует заметить при этом, что волны де Бройля нельзя рассматривать как волны вероятности. Это значит, что нельзя через вероятность проследить перемещение микрочастиц в пространстве. В противном случае вероятность стала бы «волновой» и могла бы принимать отрицательные значения, что, конечно же. не имеет смысла. М. Борн из Германии предположил, «что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности Ψ(х , у, z , t )». Эту величину называют еще волновой функцией и пси-функцией. Представляет собой она нестационарное трехмерное «волновое» поле. Волновая функция может быть комплексной, и поэтому приходится оперировать ее квадратом — |Ψ |2 = Ψ ·Ψ *, где Ψ * — функция комплексного сопряжения с Ψ . Квадрат волновой функции определяет вероятность dW нахождения микрочастицы в фиксированный момент времени в малой области пространства с объемом dV и координатами х и х + dx , у и у + dy , z и z + dz :

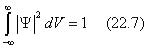
dW = |Ψ (х , у, z , t )|2 dV = |Ψ |2 dV .

Последняя фраза отражает физический смысл волновой функции. Можно к сказанному также добавить, что квадрат модуля пси-функции выражает плотность вероятности |Ψ |2 = dW / dV нахождения микрочастицы в конкретном элементарном объеме dV . И еще повторимся, что квадрат модуля волновой функции определяет вероятность пребывания микрочастицы в объеме dV .

Вероятность нахождения микрочастицы в момент времени t в объеме V равна:

. Чтобы исследуемое событие было достоверно, необходимо волновую функцию нормировать. Условие нормировки вероятностей

утверждает пребывание микрочастицы во времени и пространстве. Добавим, что волновая функция, характеризуя вероятность присутствия микрочастицы в объеме dV , должна быть конечной (вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной) и непрерывной (вероятность не может изменяться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если микросистема может находиться в состояниях, описываемых волновыми функциями Ψ1 , Ψ2 , ..., Ψn , то она может находиться в состоянии, описываемом линейной комбинацией функций

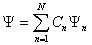, где Cn (n = 1, 2, …) — произвольные числа.

Подведем некоторые итоги изложенному: состояние микрочастицы задается с помощью волновой функции. Волновая функция — это основной носитель корпускулярно-волновой информации. Однако физический смысл имеет не сама волновая функция, а квадрат ее модуля, которым и задается интенсивность волн де Бройля.

Уравнение Шредингера

Развивая идею Луи де Бройля об оптико-механической аналогии в поведении микрочастиц, австрийский физик Э. Шредингер в 1926 г. постулировал уравнение, являющееся основным в квантовой механике. За создание квантовой теории он вместе с П. Дираком в 1933 г, был удостоен Нобелевской премии.

В современной физике вывод фундаментального уравнения квантовой механики возможен. Но является сложным. В целях упрощения рассуждений при получении уравнения Шредингера будем исходить из предположения о том, что уравнение должно соответствовать следующим соображениям. То есть проделаем научный путь, пройденный Э. Шредингером. Итак, прежде всего искомое уравнение должно быть дифференциальным уравнением в частных производных по координатам и времени и способным описать изменяющиеся в пространстве и во времени состояния микрочастицы. И, кроме того, уравнение должно быть универсальным в том смысле, что любое состояние квантовой частицы в любых физических условиях должно описываться некоторой функцией, названной пси-функцией, которая является решением этого уравнения. Это аналогично тому, как любое движение тела может быть описано с помощью уравнения

Ньютона — основного закона динамики, а любое явление электромагнетизма — с помощью уравнений Максвелла. Заметим, что эти уравнения также в свое время были постулированы. Правильность их, однако, как и волнового уравнения Шредингера, подтверждена тем, что результаты их решения совпадают с опытными данными. До настоящего времени не имело места даже единого случая отсутствия согласия между теоретическими и экспериментальными результатами. Это-то и придает названным уравнениям (как, впрочем, и ряду других) характер законов природы.

Если допустить, что квантовая частица, а это имеет место в ряде случаев, ведет себя как классическая, то полная энергия частицы массой m определяется общим уравнением

где р 2 /(2m ) — кинетическая энергия частицы; р — ее импульс; U — потенциальная энергия частицы в силовом поле, которая зависит от положения частицы в пространстве и не зависит от времени.

В начале установим вид уравнения для плоской волны де Бройля, которое описывает одно из возможных состояний свободной частицы с определенными значениями энергии

Е и импульса . В простейшем случае, когда частица движется вдоль оси Ох в сторону положительных значений координаты, такое состояние задается волновой функцией

Ψ(x , t ) = A cos( ωt – k х ). (22.8)

Выполним следующее преобразование

Известно, что ωħ = Е, 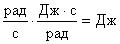и 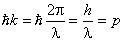, Н·с. Следовательно,

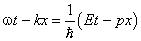. Кроме того, из курса математики известно, что e – i θ = cos θ – i sinθ . Возьмем только реальную вещественную часть этого равенства cosθ = e – θ + i sinθ = Ree – i θ . В дальнейшем обозначение действительной части Re опустим. Тогда

и другой формой уравнения (22.8) является

Найдем следующие частные производные пси-функции:

Предположим, что квантовая частица свободна в своем поведении, то есть U = 0. Это значит, что E = p 2 / 2m . Чтобы удовлетворять этому соотношению, искомое дифференциальное уравнение должно содержать производную первого порядка по времени t и производную второго порядка по координате х — уравнение должно выглядеть следующим образом:

Подставив в (22.11) выражения (22.9) и (22.10),

найдем символическое значение коэффициента пропорциональности γ:

Из Е = р 2 / (2т ) следует Е/р 2 = l /(2m ). С учетом последнего, γ = i ħ/ (2m ). Таким образом волна де Бройля является решением уравнения (22.11):

или

Это и есть уравнение Э. Шредингера для нестационарных условий движения свободной квантовой частицы массой т вдоль положительного направления координаты х.

Состояние свободной частицы в нестационарном трехмерном поле описывается псифункцией

где 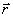— радиус вектор, 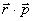— скалярное произведение двух векторов. В этом случае уравнение Э. Шредингера имеет наиболее общий вид

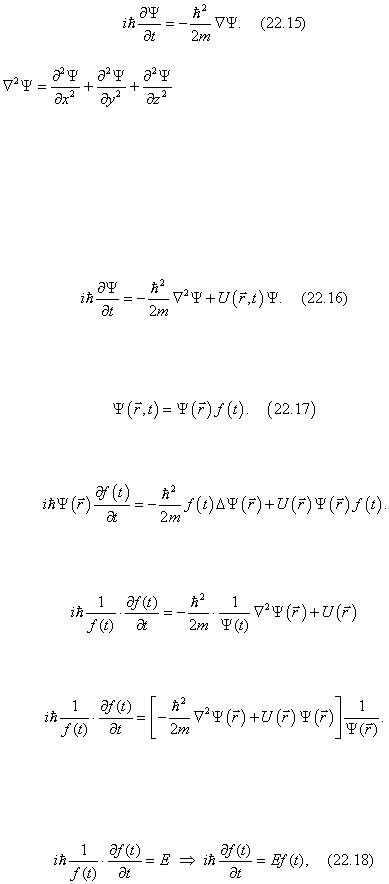
Здесь — оператор Лапласа, называемый также лапласианом.

Уравнение (22.15) получено для свободной квантовой частицы. Дальнейшее его обобщение сводится к учету возможного действия внешних сил. Для частицы,

находящейся в поле с потенциальной энергией 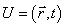, необходимо использовать полную энергию квантовой частицы Е = р 2 / (2т ) + U . Основное уравнение квантовой механики — уравнение Э. Шредингера, приобретает в этом случае вид

Решение уравнения (22.16), как известно из курса высшей математики, можно представить в виде произведения двух функций, каждая из которых зависит от и t :

Подставим (22.17) в уравнение (22.16):

Разделив обе части уравнения на произведение 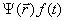, получим

или

Так как левая часть каждого из равенств зависит только от времени t , а правая —

только от радиус-вектора 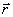, то обе части каждого из равенств должны быть равны одной и той же постоянной разделения, которую можно обозначить известной величиной Е:

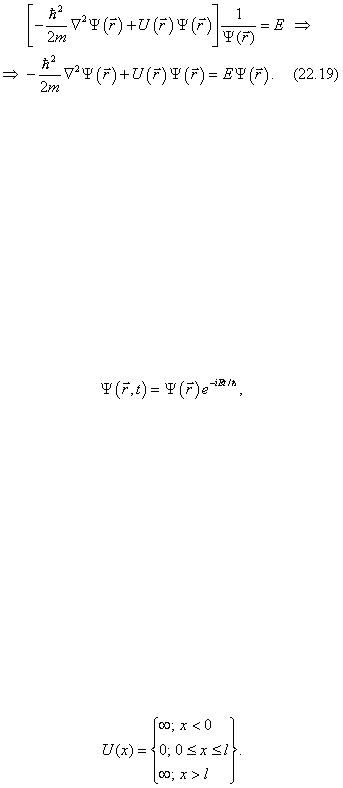
Уравнение (22.19) является уравнением Э. Шредингера для стационарного трехмерного потенциального поля.

Чтобы представить себе, по крайней мере, количественный смысл функции f (t ),

введенной соотношением (22.17), уравнение (22.18): , проинтегрируем—

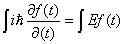. Получим i ħ [lnf (t ) – l пС ] = Et . Преобразуем i ħ ln (f (t )/ C ) = Et f (t ) / C = eEt / ( i ħ ) . Откуда f (t ) = Ce – iEt /ħ , где С — произвольная постоянная.

Таким образом, в случае нестационарного трехмерного потенциального поля состояние частицы описывается функцией

где 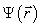— решение стационарного уравнения Шредингера (22.19).

Для того чтобы выяснить физический смысл постоянной Е, рассмотрим формулу (22.14). В этой формуле присутствует точно такое же выражение e – iEt /ħ , в котором Е представляет собой полную энергию квантовой частицы.

Микрочастица в одномерной глубокой прямоугольной «потенциальной яме»

Из уравнения Э. Шредингера следует, что характер движения квантовых частиц зависит от вида функции U (x , y , z ). Рассмотрим уравнение Э. Шредингера применительно к частице массой т, которая способна двигаться только в направлении Ох (рис. 22.2). Движение это ограничено непроницаемыми для частицы «стенками», координаты которых х 1 = 0, х 2 = l . Частица движется в потенциальном поле, ее потенциальная энергия равна:

При сформулированных условиях принято говорить, что частица находится в одномерной глубокой прямоугольной «потенциальной яме». Это простейший и реальный случай. Так, например, потенциальная энергия электрона внутри металла меньше, чем вне его. При эмиссии электрона из металла его потенциальная энергия на границе «металл— вакуум» скачком возрастает. Вот поэтому график изменения потенциальной энергии электрона в направлении вертикальной плоскости к поверхности металла вдоль оси х подобен изображению ямы с вертикальными стенками и плоским дном (рис. 22.2).

Рис. 22.2

Итак, «яма» считается одномерной, и это допущение позволяет все параметры движения, и в том числе пси-функцию квантовой частицы, рассматривать в виде функции от х. Стационарное уравнение Э. Шредингера имеет вид

Граничными условиями задачи следует считать Ψ(0) = Ψ(l ) = 0. Граничные условия формулируют невозможность попадания частицы за границы «потенциальной ямы». Поэтому при х < 0 и х > l пси-функция тождественно равна нулю, но из условий непрерывности этой функции следует, что и на границах ямы Ψ(х ) должна быть равна нулю. Итак, частица не может выбраться из «ямы», поэтому вероятность ее обнаружения за пределами «ямы» равна нулю. Поскольку начало отсчета потенциальной энергии может быть выбрано произвольно, будем считать, что потенциальная энергия рассматриваемой частицы внутри «ямы» и на ее границах при х = 0 и х = l равна нулю. При этом частица с любой кинетической энергией не может выйти за пределы «ямы» .

Из изложенного видно, что потенциальная энергия частицы является «ступенчатой» функцией. Поэтому конкретное решение задачи возможно для одного из трех участков на оси Ох. Рассмотрим участок 0 ≤ х ≤ l , то есть частица находится в пределах «потенциальной ямы». В этом случае U (х ) = 0, и уравнение Э. Шредингера принимает вид

Здесь

2mE / ħ 2 = 2mmv 2 / (2ħ 2 ) = (2πp / ħ )2 = =(2πp / (λp ))2 = (2π / λ )2 = k 2 . (22.20)

— квадрат волнового числа. И следовательно, предыдущее уравнение можно записать следующим образом:

Дифференциальное уравнение этого типа известно из теории колебаний. Составим характеристическое уравнение, соответствующее дифференциальному уравнению, в

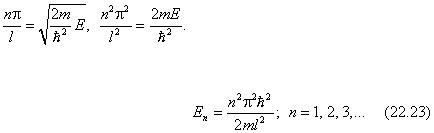
форме ρ2 + k 2 = 0. Откуда ρ 2 = –k 2 и ρ = ±ik . Так как корни характеристического уравнения мнимые, то общим решением уравнения (22.21) является пси-функция, равная

Ψ = C 1 sinkx + C 2 coskx . (22.22)

Значения постоянных С 1 и С2 следуют из (22.22) и граничных условий: Ψ(0) = 0; 0 =

C 1 sink 0 + C 2 cosk 0 = С 2 ; С 2 = 0; Ψ(l ) = 0; 0 = C 1 sinkl + C 2 coskl = C 1 sinkl ; С 1 ≠ 0 при sinkl = 0. Последнее возможно, если kl = n π , где n = 1, 2, 3,... Это значит, что на отрезке

0... l . должно укладываться целое число полуволн. Итак, k = πn / l . И поскольку согласно формуле (22.20) волновое число k = (2тЕ / ħ 2 )0,5 , то возможно равенство

Откуда кинетическая энергия квантовой частицы в «потенциальной яме» равна:

Очевидно, что в зависимости от значения числа n , которое называют главным квантовым числом, спектр энергетических состояний частицы оказывается дискретным. В таком случае говорят, что энергия квантуется, и квантованные значения ее в зонной теории называют уровнями энергии. Это значит, как Уже известно, что частица в «потенциальной яме» может находиться на определенном энергетическом уровне. Иными словами, можно сказать, что частица находится в квантовом состоянии п с энергией Е n . Согласно формуле (22.23) микрочастица в «потенциальной яме» не может иметь энергию меньше минимальной Е min = π2 ħ 2 / (2ml 2 ), n = 1, Дж. И это не случайно, так как

неопределенности х рх > ħ импульс не может иметь при этом точное, в данном случае нулевое, значение. Неопределенность импульса равна: р h / x = h / l Этому интервалу значений импульса соответствует минимум кинетической энергии Е min (Δр )2 / (2т ) = ħ 2 / (2ml 2 ). Всем же остальным уровням при п > 1 соответствует энергия, превышающая это минимальное значение.

Рассмотрим энергетические уровни, определяемые формулой (22.23). Наименьший уровень Е 1 соответствует квантовому числу п = 1. Вспомним, что значение п = 0 тождественно Ψ 0, то есть отсутствию микрочастицы. Следующий уровень имеет место при п = 2 и равен Е 2 = 4Е 1 , третий уровень — Е 3 = 9Е 1 и т. д. Очевиден вывод о том, что, во-первых, энергетические уровни распределены неравномерно и, во-вторых, чем больше значение квантового числа п, тем больше разрыв между соседними уровнями энергии (рис. 22.3).

Рис. 22.3

Из (22.23) следует, что интервал между двумя соседними уровнями энергии равен:

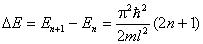. При большом п выражение (2 n + 1) / 2 п и предыдущее уравнение принимает вид

На величину интервала между соседними уровнями энергии существенное влияние оказывает размер потенциальной ямы l . Например, свободному электрону с массой т 10–30 кг в металле соответствует ширина ямы l = 10–1 м, а Е = 10–35 п , Дж. Средняя

энергия теплового движения свободных электронов равна 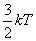и при комнатной температуре составляет 6·10–21 Дж. Таким образом, разность энергий соседних уровней очень мала по сравнению со средней величиной энергии, и поэтому можно считать, что энергетический спектр в данном случае непрерывен.

Если ширина «ямы» соизмерима с размером атома, то есть l = 10–10 м, то картина будет иной. В этом случае Е 10–17 п, Дж, что значительно (в ~104 раз) превышает энергию теплового движения микрочастиц при обычных температурах, и здесь энергетический спектр электрона дискретен. Классическая же механика не вводит ограничений на энергию этой микрочастицы, так как в классической физике Е = mv 2 /2.

Попытаемся теперь отыскать значение волновой пси-функции в зависимости от ширины «ямы» х. Равенство (22.22) с учетом полученных результатов примет вид

Условие нормировки может быть сформулировано в данном случае: