Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Педагогический Университет им. И. Н. Ульянова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ankilov

.pdf

Скачиваний:

Добавлен:

07.02.2015

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

8. Как определяется и вычисляется дивергенция векторного поля в данной точке? Что она характеризует?

4.Каков физический смысл циркуляции силового поля?

5.Как найти ротор векторного поля и что он характеризует?

6.Что означает знак (плюс или минус) потока через замкнутую поверхность в поле скоростей движущейся жидкости?

7.В каком векторном поле поток через любую замкнутую поверхность равен нулю?

8.Всякое векторное поле a(M ) порождает новое векторное поле rot a(M ) . Будет ли

это поле соленоидальным?

9.Если a(M ) = grad u(M ) , то чему равен rot a(M ) ?

10.В каком векторном поле циркуляция вдоль любого замкнутого контура равна нулю?

11.Какому уравнению удовлетворяет потенциал гармонического поля?

4.5. Задачи для самостоятельного решения

Задание 1. Найти производную скалярного поля по направлению вектора S в точке M 0

1.z ln 3x2 5y2 ; S 4i 3 j , M 0 (1, 1)

2.z arctg(xy) ; S 12i 5 j , M 0 (1, 2)

3.u ln x y2 z ; S 2i 2 j k , M 0 (1, 3, 2)

4.u x2 arctg( y z) ; S 18i 9 j 18k , M 0 (1, 1, 1)

Задание 2. Найти градиент скалярного поля в точке M 0

1. z xy12 ; M 0 (2, 3)

2.	z arcsin					x2	;	M 0 (1, 2)
2.	z arcsin					y	;	M 0 (1, 2)
						y

3.	u x		2	yz				z2	1 ;		M	0 (0, 1, 3)
3.	u x			yz				2	1 ;		M	0 (0, 1, 3)
								2
		y2 z3							1			3
4.	u				;	M				,	2,
4.	u				;	M				,	2,
			x					0	2			2
			x						2			2

Задание 3. Найти угол между градиентами скалярных полей u(x, y, z) и v(x, y, z) в точке M 0

2x yz z3 ,

xy2

; M 0 (0, 2, 1)

z 4

yz2

, v x

; M

Задание 4. Найти поток векторного поля a a(M ) через

поверхность S (нормаль к поверхности S образует острый угол с

осью Oz )

; S : z 1 x2 y2

1. a (x 2 y)i

(3y z)k

(x 0, y 0)

2. a 2xi

3yj 4zk ; S : 2x y z 1 (x 0, y 0, z 0)

a x2i

; S : x2 y 2 z 2

(0 z h)

z2 k

Ответы

3202965 512

17 15
			Ответы
	1				1
			,
	36		,
	36				27
2		,			1

	3			2 3
	3			2 3
0,1, 2
	3		3	,	3	3	,	9		2
		2		,	2		,		2
		2			2				2

Ответы

	4

Ответы

( 2)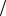3 34

h4 2

111

Задание 5. Найти поток векторного поля a a(M ) через замкнутую поверхность S в направлении внешней нормали

a yi

zj xk ; S : x y z a , x 0 , y 0 , z 0

a (x2

y2 )i

( y2 z2 )

(z2 x2 )k

; S : x 0 , x 1, y 0 ,

y 1, z 0 , z 1

3. a (x3 x)i

( y3 2 y)

(z3 3z)k

; S : x2 y2 z2 1

a (x2 yz)i

( y2 xz)

; S : x2 y2 z2 1,

(z2 xy)k

x2 y2 z2 ( z 0 )

Задание 6. Найти дивергенцию векторного поля a a(M ) в точке

M 0

1.a 2xy2i yzj 3z2 k ; M 0 (1, 2, 1)

2.a xi yj zk ; M 0 (3, 4, 5)

x2 y2


3. a	xi	yj zk	; M 0 (1, 2, 2)
3. a	x2	y2 z2	; M 0 (1, 2, 2)
	x2	y2 z2

Задание 7. Найти циркуляцию векторного поля a a(M ) вдоль

контура С в направлении, соответствующем возрастанию параметра t

a yi

xj zk

; C : x R cost, y Rsin t , z 0

x2 y2 z2

a y2 z2i

x2 z2

x2 y2k

; C : x 2cost, y 2sin t ,

z 2cos3t

a yzi

xzj

xyk ; C : x a cost, y a sin t , z bt

Задание 8. Найти ротор векторного поля a a(M ) в точке M 0

1. a 2x2 yi yz2 j xy k ; M 0 ( 1, 1, 2)

2. a x2 yzi xy2 zj xyz2k ; M 0 (0, 1, 1)

3.a x2 y2 z2 (xi yj zk ) ; M 0 ( 1, 2, 3)

4.6.Итоговый контроль

Ответы

12 5

Ответы

18125

Ответы

2 2a2b

Ответы

5, 1, 2

0, 1, 10, 0, 0

Изучив тему, студент должен:

знать:

определения скалярного поля и его основных характеристик (производная по направлению, градиент);

связь между градиентом и производной по направлению;

определения векторного поля и его основных характеристик (поток, дивергенция, циркуляция, ротор);

физический смысл потока, дивергенции, циркуляции, ротора векторного поля;

формулы Стокса и Остроградского-Гаусса в векторной форме;

простейшие векторные поля (потенциальное, соленоидальное, гармоническое) и их основные свойства;

уметь:

вычислять производную по направлению и градиент скалярного поля;

112

вычислять поток, дивергенцию, циркуляцию и ротор векторного поля;

применять формулу Остроградского-Гаусса для вычисления потока векторного поля через замкнутую поверхность;

применять формулу Стокса для вычисления циркуляции векторного поля;

иметь представление:

о конкретных физических полях;об операторе Гамильтона и правилах действий с ним.

4.6.1. Тест

1. Градиент скалярного поля U x3 y3 z3 3xyz перпендикулярен оси O z в точках, координаты которых удовлетворяют равенству:

а)	x zy2 ;
б)	y2 xz ;
в)	z2 xy ;
г)	y xz2 ;
д)	x2 yz .

2.Если s grad U (x, y, z), то производная Us равна:

а) 0; б) s ;

в) grad U ; г) grad U ; д) grad U .

3.Если r xi y j zk , то grad r равен:

а) r ; б) r / r ;

в) r r ;

г) r ; д) r / r 2 .

4.Выберите верные утверждения. Если в пространственной односвязной области D задано потенциальное поле a a(M ) , то:


а)	rot	a	(M ) 0 в каждой точке M D ;
б) в области D нет источников и стоков;
в) циркуляция Г (									, d		) 0 , где L – любой замкнутый контур, лежащий в D;
в) циркуляция Г (								a	, d	r	) 0 , где L – любой замкнутый контур, лежащий в D;
						L
г)	поток K (				,		)d 0 , где S – любая замкнутая поверхность, лежащая в D;
г)	поток K (			a	,	n	)d 0 , где S – любая замкнутая поверхность, лежащая в D;
			s

д) интеграл (a, d r) не зависит от линии интегрирования, соединяющей точки

А и В.

113

5.Выберите верные утверждения. Если в пространственной односвязной области D задано соленоидальное поле a a(M ) , то:

(см. варианты ответов на вопрос 4).

6.Поток вектора a 3xi y j zk через сферу x2 y 2 z 2 1 в направлении внешней

нормали равен:

а)

б)

3π;

в)

4π / 3;

г)

4π;

д)

Если

xi y

, а

– постоянный вектор, то дивергенция вектора

равна:

а)

б)

в)

;

г)

д)

Абсолютная величина

циркуляции вектора

x2 i y 2

z 2

вдоль окружности

x2 y 2

z 2 1, x y z 1 равна:

а)

π;

б)

в)

2π;

г)

д)

Заданное в односвязной области D векторное поле

(M ) будет гармоническим,

если:

а)

div

(M ) 0 ;

б)

div

(M ) 0, rot

(M ) 0 ;

в)

rot

(M ) 0 ;

г)

div

(M ) 0,

(M ) grad U (M ) ;

д)

rot

(M ) 0,

(M ) grad U (M ) .

10.

Выберите верные утверждения. Если в каждой точке M (x, y, z) области D заданы

скалярная функция U U (M ) и вектор-функция

(M ) , то:

а)

rot grad U (M ) 0 ;

б)

rot div

(M ) 0 ;

в)

div grad U (M ) 0 ;

г)

div rot

(M ) 0 ;

д)

grad rot

(M ) 0 .

114

4.6.2. Задачи Образцы решения задач

Задача 1. Найти производную скалярного

поля u(x,y,z)= x2

arctg y z

точке

М (1,1,1) по направлению вектора

18i

9 j 18k .

Решение.

Вычислим

grad u

точке

М (1,1,1) : grad u

u ,

2x,

, grad u (М) =

1 ,

1 .

y z 2

1 y z 2

18,9,18 .

Найдем

направляющие

косинусы

вектора

Так

как

182

2 27, то cos 18

2 , cos

1 ,

cos 18

2 .

Производную по направлению вычисляем по формуле

u cos u cos u cos :

us M 2 23 15 13 15 23 1715 .

Задача 2. Найти угол между градиентами скалярных полей u x, y, z 2x yz z3 ,

v x, y, z

xy2

в точке М (0,2,1).

z 4

Решение. Найдем градиент скалярного поля u x, y, z в точке М:

grad u

, u

2, z,3z

2 y ,

Аналогично,

grad u M 2, 1,1 .

grad v

v ,

v , v

y 2

, 2xy ,

4xy2 ,

y z

z 4

grad v M 4,0,0 .

Пусть – угол между векторами grad u (М) и grad v (М), длины этих векторов. Тогда

cos	grad u(M ), grad v(M )		2 4 1 0 1 0
	grad u(M )	grad v(M )	2 2 1 2 12	4

arccos 22 4 .

grad u(M ) , grad v(M ) –

22 , следовательно,

Задача
	3. Найти поток векторного поля a 3xi	2 yj zk через часть плоскости
x y 2z 1,	расположенную в первом октанте (нормаль образует острый угол с осью Oz).

115

Решение. Поток вектора a P,Q, R через поверхность S определяется формулой (4.9)

K Pdydz Qdxdz Rdxdy.

В данном случае P 3x, Q 2 y, R z, S – треугольник (рис. 4.7). Для вычисления поверхностного интеграла воспользуемся формулой (3.33)

K R zx P z y Q dxdy.

По условию нормаль образует острый угол с осью Oz, поэтому перед интегралом выбран знак «+».

1/2

y =1–x

Рис. 4.7

Рис. 4.8

Из уравнения плоскости

x y 2z 1

находим: z

1 1 x y ,

1 .

Подставляем полученные значения в подынтегральное выражение:

1 x y 3x

2 y

dxdy

и вычисляем двойной интеграл как повторный (рис. 4.8):

1	1 x				y				1				1				1		y 2			1 x						1				1					1 x 2
1	1 x				y				1				1				1		y 2			1 x						1				1					1 x 2
K dx			x								dy			x			y							dx x									1		x						dx
K dx			x		2				2		dy			x			y		4					dx x								2	1		x			4			dx
0	0				2				2				0				2		4			0						0				2						4
0	0												0									0						0								1
1		2		1			x			1		x		x	2		1		3		2				3					3			x	3				3	2			1
1															2		1																	3

x x																dx				x						dx									x								.
x x				2		2				4		2		4		dx			4	x					4	dx				4			3		x			4	3			2	.
0				2		2				4		2		4			0		4						4					4			3			0		4	3			2
0																	0												1							0
																											z												2
Задача	4.		Найти					поток					векторного					поля									z								x y j x				2	y z k через
Задача	4.		Найти					поток					векторного					поля					a e						2		x i				x y j x					y z k через
																													2
замкнутую поверхность S : x2 y2														z2 2x 2 y 1 (нормаль внешняя).

Решение. Поскольку S – замкнутая поверхность, то можно воспользоваться формулой Остроградского-Гаусса (4.13), согласно которой поток

K div a dV ,

116

где Т – область, ограниченная поверхностью S, div a P Q R – дивергенция вектора

x y z

aP, Q, R .

Вданном случае P ez 12 x , Q x y , R x2 y z , следовательно,

			z		1					x	y		x		2	y z	1			1
			z		1										2		1			1
div a		e				x												1	1		,
div a		e			2	x			y			z					2	1	1	2	,
	x				2				y			z					2			2
	K div							dV		1 dV			1	dV			1 V .
	K div						a	dV		1 dV			1	dV			1 V .
				T						T	2		2		T		2

Остается найти объем V тела Т. Выясним, что собой представляет это тело. С этой целью преобразуем уравнение поверхности S, выделяя полные квадраты:

x2 y2 z2 2x 2 y 1,

x2 2x 1 y2 2 y 1 z2 1 2 ,x 1 2 y 1 2 z2 1.

Таким образом, поверхность S – сфера радиуса R=1 с центром в точке (1, 1, 0), тело Т – шар, ограниченный этой сферой. Его объем V 43 . Тогда K 12 V 12 43 23 .

Задача 5. Найти циркуляцию векторного поля a xzi y j xk вдоль контура С: x sin t , y cos t , z cos t (в направлении, соответствующем возрастанию параметра t).

Решение. Из уравнений контура С следует, что изменению параметра t от 0 до 2π соответствует однократный обход этого контура. Циркуляция Г определяется формулой

(4.15)

Г Pdx Qdy Rdz .

Поскольку линия С задана параметрически, то для вычисления интеграла воспользуемся формулой (3.11) (точнее, ее обобщением на случай пространственной кривой). Учитывая,


что P xz, Q y, R x, x								(t) cos t				, y (t) sin t,	z (t) sin t, будем иметь
	2	P x Q y R z dt							2	sin t cos t cos t cos t( sin t) sin t( sin t) dt
Г		P x Q y R z dt								sin t cos t cos t cos t( sin t) sin t( sin t) dt
	0								0
2	cos2 t											2	2	1	2
	cos2 t				sin t cos t sin t sin 2					t dt cos2 td(cos t) cos td (cos t)				1	1 cos 2t dt
0												0	0	2	0
			3	t	cos	2					2	.
			3			2					2
cos							t 1 t sin 2t
		3			2		2	4
		3			2		2	4			0

Расчетное задание

Задача 1. Найти производную скалярного поля u (x, y, z) в точке М по направлению вектора s.

u (x2 y2

z 2 )3 / 2 ,

, M (1, 1, 1) .

u x ln(z 2

y2 ),

, M (2, 1, 1) .

u x2 y

xy z 2 ,

, M (1, 5, 2) .

117

4. u y ln(1 x2 ) arctg z, s 2i 3 j 2k, M (0, 1, 1) .

5.u x(ln y arctg z), s 8i 4 j 8k, M ( 2, 1, 1) .

6.u ln(3 x2 ) xy2 z, s i 2 j 2k, M (1, 3, 2) .

7. u sin(x 2 y) xyz, s 4i 3 j, M ( / 2, 3 / 2, 3) .

8.u x2 y2 z ln(z 1), s 5i 6 j 2 5k, M (1, 1, 2) .

9.u x3 y2 z 2 , s j k, M (1, 3, 4) .

10.u xy 9 z 2 , s 2i 2 j k, M (1, 1, 0) .

Задача 2. Найти угол между градиентами скалярных полей u (x, y, z) и v (x, y, z) в точке М.

	u	yz			2					x		3					2									3											1						1
1.							, v							6 y						3 6z							, M							2,							,					.
1.				2			, v							6 y						3 6z							, M							2,							,					.
		x		2						2																													2
		x								2																													2					3
			2					3				4	6							6			3											1						3
2.	u x				yz				, v																	, M						2,			,							.
2.	u x				yz				, v																	, M						2,			,							.
													x						9 y					z										3						2
													x						9 y					z										3						2
		z3														3					y	3				4z			3							1									3
3.	u						, v			9 2				x																		, M							, 2,									.
3.	u				2		, v			9 2				x																		, M							, 2,									.
		xy			2															2		2						3								3									2
		xy																		2		2						3								3									2
	u			z								3			4					1														1
4.									, v														, M 1, 2,															.
4.			3			2			, v														, M 1, 2,															.
		x	3		y	2						x			y						6z														6
		x			y							x			y						6z														6
	u	x2					, v				x3			6 y				3								z	3		M											1					1
5.																				3 6								,							2,								,						.
5.					2															3 6								,							2,								,						.
		yz			2					2																														2							3
		yz								2																														2							3
		z 2													2					y2											2						1								2
6.	u						, v			3 2x												3 2							z				,	M						, 2,									.
6.	u				2		, v			3 2x												3 2							z				,	M						, 2,									.
		xy			2															2																	3								3
		xy																		2																	3								3
	u	xz			2		, v			6 6x					3	6 6 y							3		2z					3		, M							1					1
7.																																										,						, 1 .
7.																																										,						, 1 .
			y																																				6						6
			y																																				6						6
		yz			2							6						6				2									1					1						1
8.	u						, v																	,	M									,						,					.
8.	u						, v																	,	M									,						,					.
			x								2x					2 y						3z										2					2						3
			x								2x					2 y						3z										2					2						3

9.	u	xy2	, v 3 2x2
		z 2

10.	u	x3 y 2		, v	3	4
		z			x	y

y 2	3 2 z		2			1		, 2,	2
	3 2 z			, M				, 2,		.
2						3			3
2						3			3
1					1
	,	M 1,		2,			.
	,	M 1,		2,			.
6 z					6
6 z					6

Задача 3. Найти поток векторного поля a через часть плоскости Р, расположенную в первом октанте (нормаль образует острый угол с осью Oz).

1.a 2xi y j zk, P : 2x 3y z 1 .

2.a xi 3y j 2zk, P : x y z 1.

3.a xi 2 y j zk, P : x / 2 y z 1.

4.a xi y j zk, P : x y / 2 z / 3 1.

118

5.a xi y j 6zk, P : x / 2 y / 3 z 1.

6.a xi y j zk, P : 2x y / 2 z 1.

7.a xi 3y j 8zk, P : x 2 y z / 2 1.

8.a xi y j zk, P : 2x 3y z 1.

9.a xi 9 y j 8zk, P : x 2 y 3z 1 .

10.a 2xi y j 4zk, P : x / 3 y z / 2 1.

Задача 4. Найти поток векторного поля a через замкнутую поверхность S (нормаль

внешняя).

ez 2x i ex

e y

, S : x y z 1, x 0, y 0, z 0 .

3z 2 x i ex 2 y

2z xy

, S : x2 y 2 z 2 , z 1, z 4 .

ln y 7x i sin z 2 y

e y 2z

, S : x2 y2

2x 2 y 2z 2 .

cos z 3x i x 2 y

3z y2

, S : z2

36 x2 y2 , z 6 .

e z x i xz 3y

z x2

, S : 2x y z 2, x 0, y 0, z 0 .

6x cos y i ex

2 y 3z

, S : x2

z2 , z 1, z 2 .

a 4x 2 y

2x 3 .

i ln z 4 y j x

k, S : x

z i 4 y

S : z2

4 x2 y2 , z 3 .

xyk

z x i x y

y2 z

, S : 3x 2 y z 6, x 0, y 0, z 0 .

10.

yz x i x2

xy2 z

S : x2 y2

2z .

Задача 5. Найти циркуляцию векторного поля

вдоль контура С (в направлении,

соответствующем возрастанию параметра t).

yi x

C : x

cos t, y

cos t, z sin t .

y z i z x

x y

C : x cos t, y sin t, z 2(1 cos t) .

x2 i y

C : x cos t, y

2 sin t / 2, z

2 cos t / 2 .

2zi x

C : x 2cos t,

y 2sin t, z 1.

5.a 2 yi 3x j xk, C : x 2cos t, y 2sin t, z 2 2cos t 2sin t .

6.a zi y2 j xk, C : x 2 cos t, y 2sin t, z 2 cos t .

7.a zi x j xzk, C : x 5cos t, y 5sin t, z 4 .

8.a 3yi 3x j xk, C : x 3cos t, y 3sin t, z 3 3cos t 3sin t .

9.a xyi x j y2 k, C : x cos t, y sin t, z sin t .

10.a ( y z) i (z x) j (x y) k, C : x 2cos t, y 2sin t, z 3(1 cos t) .

119

ГЛАВА 5. РЯДЫ

В данной главе будут рассмотрены ряды, являющиеся обобщением понятия суммы на случай бесконечного числа слагаемых. Ряды представляют собой важный математический аппарат, применяемый для вычислений и исследований как в различных разделах самой математики, так и во многих ее приложениях.

5.1.Числовые ряды

5.1.1.Определение ряда и его сходимость

Определение 5.1.1. Пусть дана бесконечная числовая последовательность u1 , u2 , ..., un , ... . Выражение вида

u1 u2 ... un ... un

n 1

называется числовым рядом. Числа u1 , u2 , ..., un , ... называются членами ряда, член произвольным номером – общим или n-м членом ряда.

Определение 5.1.2. Конечная сумма

Sn u1 u2 ... un uk ,

k 1

(5.1)

un с

слагаемыми которой являются первые n членов ряда (5.1), называется n-й частичной суммой данного ряда, а ряд

un 1 un 2 un 3 ... uk

k n 1

называется n-м остатком ряда (5.1).

Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную числовую последовательность Sn :

S1 , S2 , S3 , ..., Sn , ... .

(5.2)

Определение 5.1.3. Если последовательность частичных сумм (5.2) имеет конечный

предел S, т. е. lim Sn S , то ряд (5.1) называется сходящимся, а число S называется суммой

ряда (5.1).

В этом случае пишут: S u1 u2 ... un ..., или S un . Таким образом, символ

n 1

un используется как для обозначения самого ряда (5.1), так и для обозначения его суммы,

n 1

если он сходится.

Если последовательность (5.2) не имеет конечного предела (расходится), то ряд (5.1) называется расходящимся. Расходящийся ряд суммы не имеет.

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.02.201581.23 Кб178.docx
#
20.09.2019105.47 Кб48_beR.doc
#
07.02.2015282.72 Кб499-105.docx
#
06.02.2015219.14 Кб20Abl_BH_Met_Flash.doc
#
06.02.201526.62 Кб14about_myself_1.doc
#
07.02.20152.14 Mб41Ankilov.pdf
#
18.11.2019159.23 Кб5Arkhivovedenie-1.doc
#
13.08.2019157.18 Кб5B7.doc
#
20.12.2018451.58 Кб23Batychko_V_T_Trudovoe_pravo_v_voprosah_i_otveta....doc
#
26.04.2019304.13 Кб10bilety_po_yazykoznaniyu_Vosstanovlen.doc
#
05.08.201967.37 Кб4Bilet_ps.docx