Экзаменационный билет №13
1. Понятие случайного сигнала «белый шум». Спектральная плотность мощности и корреляционная функция «белого» и небелого шума. Понятие квазибелого шума.
Если спектральная плотность мощности постоянна во всей области частот, то такой сигнал называют белым шумом.
Под «небелым шумом» мы понимаем случайный процесс, ковариационная функция которого не равняется нулю для несовпадающих моментов времени. В наиболее общей постановке задачи каждое наблюдение может содержать белый шум, небелый шум марковского типа, не содержать шума вообще или быть некоторой комбинацией трех рассмотренных возможностей. Поэтому в дальнейшем под термином «небелый шум» понимается наличие шума марковского типа или отсутствие шума вообще в одном или нескольких измерениях.
Квазибелый шум – это шум с равномерным не зависящим от частоты распределением спектральной мощности в определённом диапазоне пространственных частот.
???Процесс является марковским, если следующее состояние точки зависит только от настоящего (текущего) состояния и не зависит от прошлых состояний.????
Слева спектральная плотность, справа корреляционная функция
2. Структура сверточного кодера, как цифрового фильтра. Диаграмма состояний сверточного кодера, как конечного автомата. Импульсная характеристика сверточного кодера и порядок ее расчета.
Рис. 1. Сверточный кодер
Рассмотрим работу кодера рис. 1 на двух примерах, при поступлении на его вход двух последовательностей информационных символов.
1. В этом примере на вход кодера подана последовательность информационных символов: 1000. Реакция кодера на этот входной сигнал является важной характеристикой, которая называется импульсной характеристикой кодера (по аналогии с названием «импульсная характеристика линейной цепи», которая является реакцией цепи на импульс).
Предположим, что к моменту поступления этой входной последовательности все ячейки регистра сдвига кодера находились в состоянии 0. Тогда, после поступления 1 в первую ячейку регистра на выход кодера через коммутатор будет считана кодовая последовательность 11. Затем, в первую ячейку регистра записывается второй информационный символ входной последовательности, т.е. 0, а ее первый символ 1 перейдет во вторую ячейку регистра, в результате чего через коммутатор на выход поступит вторая кодовая последовательность 10. После поступления на вход кодера третьего информационного символа 0 в ячейках регистра будет записана последовательность 001 и на выходе коммутатора появится третья кодовая последовательность 11.
Таблица 1
№ тактового интервала k |
Входные символы |
Содержимое ячеек регистра |
Символы на контактах коммутатора (на выходе) |
|||
|
|
1 |
2 |
3 |
Верхний |
Нижний |
|
Исходное состояние |
0
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0
|
0 |
1 |
0 |
1 |
0 |
2 |
0 |
0 |
0 |
1 |
1 |
1 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
После поступления на вход кодера четвертого информационного символа 0 в ячейках регистра будет записана последовательность 000 и на выход через коммутатор поступит четвертая кодовая последовательность 00. Рассмотренный пример характеризует таблица 1 и рис. 5.
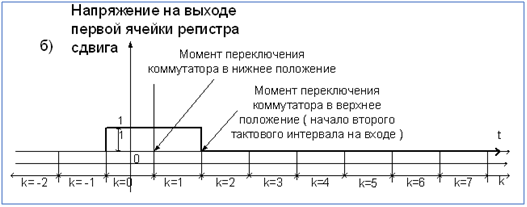
Рис.5 а) Сигнал на входе кодера, изображенного на рис. 1; б) Напряжение на выходе первой ячейки регистра; в) Сигнал на выходе: импульсная характеристика свёрточного кодера
На рис. 5 введены следующие обозначения: величина тактового интервала для входного сигнала;
- величина тактового интервала для выходного сигнала.
На рис. 5в изображена импульсная характеристика кодера – реакция на единичный символ, подаваемый на вход кодера.