Экзаменационный билет №14

1. Математическая модель случайного узкополосного сигнала в виде квадратурных колебаний.Плотность распределения вероятности мгновенных значений узкополосного случайного сигнала. Закон распределения вероятности огибающей и закон распределения вероятности фазы узкополосного случайного сигнала.

Узкополосным будет и сигнал, отличающийся фазой «быстрого» сомножителя. Наиболее общую математическую модель узкополосного сигнала можно получить, составив линейную комбинацию вида

Обе входящие сюда функции времени As(t) и Bs(t) являются низкочастотными в том смысле, что их относительные изменения за период высокочастотных колебаний достаточно малы. Функцию As(t) принято называть синфазной амплитудой узкополосного сигнала s(t) при заданном значении опорной частоты w0 а функцию Bs(t) — его квадратурной амплитудой.

Плотность распределения вероятности мгновенных значений узкополосного случайного сигнала.

Одномерная плотность вероятности огибающей. Поскольку функция не зависит от угла на основании выражений (одномерную плотность вероятности огибающей) и (2мерную плотность вероятности огибающей)

плотность вероятности огибающей равна:

(7.61)

Здесь также целесообразно перейти к безразмерной переменной z=U/σx относительно которой (7.62)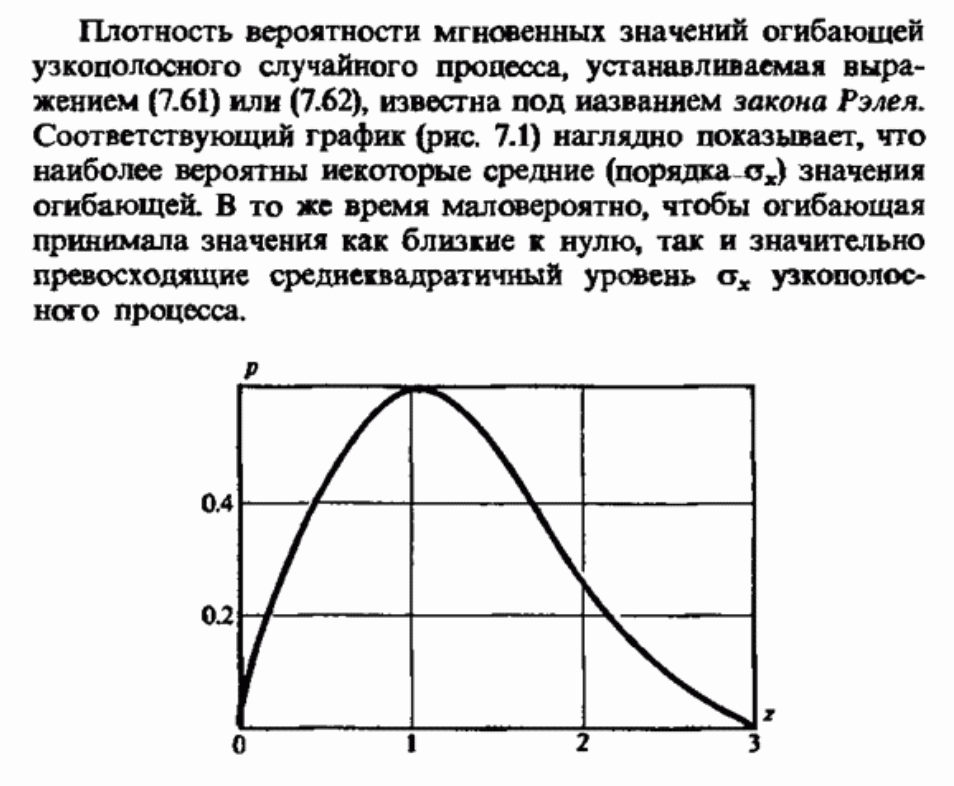

Плотность вероятности мгновенных значений огибающей узкополосного случайного процесса, устанавливаемая выражением (7.61) или (7.62), известна под названием закона Рэлея. Соответствующий график (рис. 7.1) наглядно показывает, что наиболее вероятны некоторые средние (порядка σx значения огибающей. В то же время маловероятно, чтобы огибающая принимала значения как близкие к нулю, так и значительно превосходящие среднеквадратичный уровень σx узкополосного процесса.

Рис. 7.1. График плотности вероятности случайной величины, распределенной по закону Рэлея (по оси абсцисс отложен безразмерный аргумент z=U/σx)

Распределение огибающей, характеризуемое плотностью вероятности (7.61), называется распределением Рэлея. Интегрирование двумерной плотности вероятности , определяемой выражением , по переменной А дает одномерную плотность вероятности фазы

2. Статистические критерии оптимального приема. Априорная вероятность передачи сигналов и апостериорная вероятность приема сигналов. Вероятность ошибки. Средний риск. Байесовский критерий минимума среднего риска.

Критерии оптимального приема

Количественно помехоустойчивость определяется мерой соответствия принятого сообщения переданному. Эта мера качества решения из-за случайного характера помех всегда является статистической и определяется потребителем сообщения (степенью чувствительности потребителя к тем или иным искажениям).

Оптимальный приемник (оптимальное правило решения) обеспечивает наилучшее качество решения, то есть обеспечивает минимум искажений переданного сообщения в соответствии с мерой качества, заданной потребителем.

Оптимальное значение меры качества, которое достигается приемником в процессе оптимизации, называется критерием оптимальности приема.

Байесовский приемник.

При приеме дискретных сигналов в качестве меры помехоустойчивости обычно используется средний риск R_ср, тогда критерием оптимальности является min {R_ср}.

Пij - функция потерь (риск потребителя) при приеме aj , когда передавался сигнал Si ; при этом i = j соответствует правильному приему.

M -число передаваемых сигналов.

Пример при М=2:

1. Пожар – пожарной тревоги нет (пропуск сигнала, ошибка первого рода). Плата (потери, риск) большая.

2. Пожара нет - пожарная тревога есть (ложная тревога, ошибка второго рода). Плата (потери, риск) малая.

Приемник, работающий по этому критерию, называется байесовским, а правило решения - байесовским правилом.

Априорная вероятность передачи сигналов и апостериорная вероятность приема сигналов. Вероятность ошибки. Средний риск. Байесовский критерий минимума среднего риска.

В n-мерном пространстве случайный сигнал z(t) характеризуется зет-мерной плотностью вероятностей вектора z : w (z). Ее можно рассматривать как плотность вероятности коэффициентов разложения z(t) по любому ортонормированному базису. Если передается некоторый символ b_i, т. е. посылается сигнал u_i(t), то можно определить условную n-мерную плотность вероятности w{z|b_i} - функцию правдоподобия i-й гипотезы (i = 0, 1, ..., m - 1)

Пусть на вход демодулятора в течение тактового интервала 0-Т приходит некоторый элемент сигнала z(t). Предположим, что демодулятор принимает при этом решение, что передан символ b_i. Вероятность того, что это решение правильно, очевидно, равна условной вероятности того, что действительно передавался символ b_i, при условии прихода реализации элемента сигнала z(t), P(b_i|z). Ее называют обычно апостериорной вероятностью символа b_i (т. е. вероятностью, определенной после опыта, заключающегося в наблюдении и анализе сигнала z(t)).

Очевидно, что вероятность правильного приема будет максимальной в такой решающей схеме, которая относит всякую реализацию элемента приходящего сигнала z(t) к той области B̂_i для которой апостериорная вероятность P(b_i|z) максимальна. Другими словами, критерий идеального наблюдателя обеспечивается решающей схемой, построенной по правилу максимума апостериорной вероятности - решение b_i принимается в том случае, если выполняется система из m-1 неравенств:

Согласно известной формуле Байеса

Р (b_j|z) = [Р (b_j) w (z|b_j)/w (z)], (6.5)

где P(b_j) - априорная вероятность передачи символа b_j (т. е. та вероятность, которая имеет место до наблюдения и анализа, определяемая статистикой источника сообщения и правилом кодирования).

Подставив (6.5) в и учитывая, что w(z)-безусловная плотность вероятности, не являющаяся функцией j, можно записать правило решения по критерию идеального наблюдателя в следующей форме:

Р (b_i) w(z|b_i) > P (b_j) w (z|b_j) ; i = 0, 1, ... , m - 1 ; j≠i, (6.6) или сокращенно max[P (b_i)w (z|b_i)].

Для двоичной системы правило (6.6) сводится к проверке неравенства Р (1) w (z|1) > Р (0) w (z|0), (6.7)

при выполнении которого регистрируется символ 1, а при невыполнении - 0.

Условный риск: Усреднив условный риск R_i по всем символам b_i, получим величину, называемую средним риском:

Критерий минимального среднего риска заключается в том, что оптимальной считается решающая схема, обеспечивающая наименьшее значение среднего риска R_cр. Приемник, работающий по такому критерию, называют байесовским.