2. Дисперсия случайного сигнала. Определение, формулы расчета для дискретных и непрерывных сигналов, физический смысл дисперсии, единицы измерения.

Дисперсия случайного сигнала.

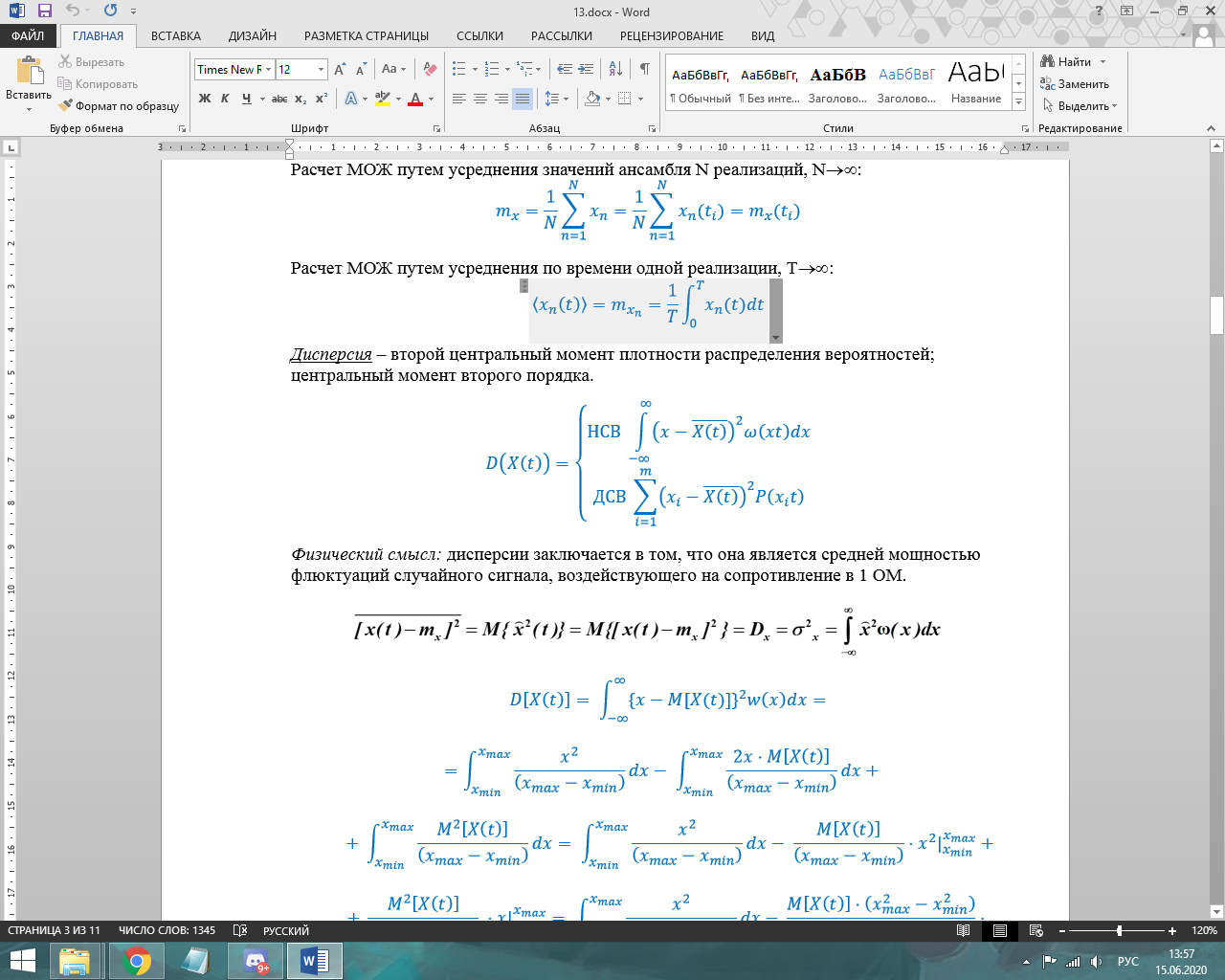
Дисперсия – второй центральный момент плотности распределения вероятностей; центральный момент второго порядка.Определение, формулы расчета для дискретных и непрерывных сигналов, физический смысл дисперсии, единицы измерения.

Физический смысл: дисперсии заключается в том, что она является средней мощностью флуктуаций(любое случайное отклонение какой-либо величины) случайного сигнала, воздействующего на сопротивление в 1 ОМ.

Экзаменационный билет №12

1. Понятие корреляции случайного сигнала. Определение, формулы расчета для дискретных, непрерывных и эргодических сигналов. Особенности АКФ эргодического сигнала. Физический смысл автокорреляционной функции случайного сигнала.

Корреляционной (ковариационной, автоковариационной, автокорреляционной) функцией случайного процесса X(t) называется неслучайная функция двух аргументов K(t1; t2), которая при каждой паре значений {t1, t2} равна корреляционному моменту соответствующих сечений X(t1) и X(t2):

Свойства:

1. Корреляционная функция при одинаковых значениях аргументов равна дисперсии с.п.

2. Корреляционная функция не меняется относительно замены аргументов, т.е. является симметричной функцией относительно своих аргументов:

3. Если к случайному процессу прибавить неслучайную функцию, то корреляционная функция не меняется, т.е. если , то . Другими словами является периодической функцией относительно любой неслучайной функции.

4. Модуль корреляционной функции не превосходит произведения ср.кв.о., т.е.

5. При умножении с.п.X(t) на неслучайный множитель её корреляционная функция умножится на произведение f(t1)*f(t2), т.е., если , то

Корреляционная функция стационарного эргодического случайного сигнала.

Корреляционной функцией случайного процесса X(t) называют неслучайную функцию двух аргументов Rx(t1,t2) которая для каждой пары произвольно выбранных значений аргументов (моментов времени) t1 и t2 равна математическому ожиданию произведения двух случайных величин соответствующих сечений случайного процесса:

Формула расчета и физический смысл интервала корреляции.

"интервал корреляции" или "время корреляции", под которыми понимается величина временного сдвига, при превышении которого корреляцией можно пренебречь в условиях конкретного эксперимента.

Тау - интервал времени; Знак модуля введен для учета случаев, когда R(тау) принимает отрицательные значения.

Основание прямоугольника называется интервалом корреляции. На этом интервале можно предсказать случайный сигнал (линейный тренд).

2. Синтез оптимального приемника дискретных сообщений при нормальной помехе в канале с использованием отношения правдоподобия. Алгоритм работы и структурная схема когерентного корреляционного приемника бинарных сигналов.

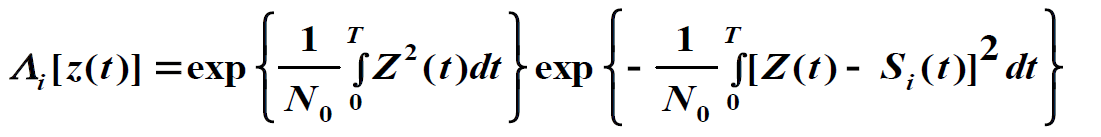
Алгоритм работы и структурная схема когерентного корреляционного приемника бинарных сигналов:

На входе демодулятора действует колебание z(t) в виде аддитивной смеси сигнала

или s0(t) (при передаче «0») + n(t) = z0(t)

или s1(t) (при передаче «1»)] + n(t) = z1(t)

с реализацией шумового гауссова процесса n(t)= N(0,σ).

Задача демодулятора состоит в принятии решения о переданном канальном символе («0» или «1») на основе анализа этого колебания на интервале длительности сигнала Т.

На выходе интегратора напряжение имеет вид суммы линейно нарастающей функции (при передаче "1") или константы 0 (при передаче "0") с шумовой составляющей.

Решающее устройство (РУ - компаратор) активируется стробирующими импульсами («kT») в моменты окончания каждого сигнала

(такта) и сравнивает отсчеты выходного напряжения интегратора с порогом.

Если отсчет превышает порог, то на выходе компаратора

формируется высокий потенциал (сообщение «1»), в противном случае - нулевой потенциал (сообщение «0»).