
- •Экзаменационный билет №1
- •1. Статистические свойства квадратурных компонент случайного узкополосного гауссова сигнала, его огибающей и фазы.
- •Экзаменационный билет №2
- •1. Модели и классификация каналов телекоммуникаций. Каналы связи с помехами. Понятие переходной вероятности канала. Вероятностные характеристики дискретного симметричного канала без памяти.
- •Экзаменационный билет №3
- •1. Оптимальный прием сигналов на фоне помех. Критерий идеального наблюдателя. Структурная схема идеального приемника Котельникова.
- •Экзаменационный билет №4
- •1. Вероятностные характеристики случайных сигналов. Физический смысл дисперсии и акф эргодического сигнала.
- •Экзаменационный билет №6
- •1. Плотность распределения вероятности мгновенных значений случайного сигнала: возможные графики одномерной прв, двумерная, многомерная.
- •2. Согласованный фильтр. Импульсная характеристика согласованного фильтра и ее связь с временной формой согласованного с ней сигнала. Описание и форма сигнала на выходе согласованного фильтра.
- •Экзаменационный билет №7
- •Математическая модель узкополосного случайного сигнала в виде комплексного колебания.
- •Экзаменационный билет №8
- •1. Корреляционная функция случайного процесса. Определение и основные свойства, формулы расчета для дискретных сигналов, для эргодических непрерывных сигналов.
- •Экзаменационный билет №9
- •1. Определение количества информации по Шеннону. Энтропия источника случайных сообщений. Свойства энтропии. Энтропия двоичного источника.
- •2. Корреляционная функция стационарного эргодического случайного сигнала. Формула расчета и физический смысл интервала корреляции.
- •Экзаменационный билет №10
- •Понятие спектральной плотности мощности случайного сигнала.
- •Теорема Винера-Хинчина.
- •Принцип помехоустойчивого кодирования канала.
- •Экзаменационный билет №11
- •1. Количественное измерение информации. Энтропия дискретного источника и ее свойства. Энтропия двоичного источника.
- •2. Дисперсия случайного сигнала. Определение, формулы расчета для дискретных и непрерывных сигналов, физический смысл дисперсии, единицы измерения.
- •Алгоритм работы и структурная схема когерентного корреляционного приемника бинарных сигналов:
- •Экзаменационный билет №13
- •1. Понятие случайного сигнала «белый шум». Спектральная плотность мощности и корреляционная функция «белого» и небелого шума. Понятие квазибелого шума.
- •2. Структура сверточного кодера, как цифрового фильтра. Диаграмма состояний сверточного кодера, как конечного автомата. Импульсная характеристика сверточного кодера и порядок ее расчета.
- •Экзаменационный билет №14
- •Плотность распределения вероятности мгновенных значений узкополосного случайного сигнала.
- •Экзаменационный билет №15
- •Экзаменационный билет №16
- •Автокорреляционная функция (акф) – второй смешанный центральный момент двумерной плотности распределения вероятностей; центральный смешанный момент второго порядка.
- •Экзаменационный билет №18
- •1. Синтез оптимального приемника на согласованных фильтрах. Алгоритм работы и структура оптимального приемника на согласованных фильтрах для бинарных сигналов.
- •2. Эффективное кодирование источника. Словарное кодирование. Алгоритм Лемпеля-Зива. Порядок составления словаря и порядок формирования кодовых символов для передачи по каналу.
- •Экзаменационный билет №20
- •1. Формирователь модулирующих символов (фмс) для сигналов кам16. Сигнальное созвездие кам-16. Понятие о коде Грея.
- •Условная энтропия между входом и выходом в канале и взаимная информация входа и выхода
- •Экзаменационный билет №21Классификация случайных сигналов по виду закона распределения. Нормальный закон: формула одномерной прВинтеграл вероятности
- •Экзаменационный билет №22
- •2. Модели непрерывных каналов с аддитивным шумом: с постоянными параметрами, с неопределенной фазой, с общими и частотно-селективными замираниями.
- •Экзаменационный билет №23
- •1. Блочный код Хэмминга (7,4). Структура проверочной матрицы для систематического кода. Принцип кодирования с использованием проверочной матрицы.
- •Экзаменационный билет №24
- •1. Блочный код Хэмминга (7,4). Проверочная матрица систематического кода и получение синдрома кодового слова. Принцип синдромного декодирования систематического блокового кода.
- •2. Модели дискретных каналов. Математическое описание несимметричного канала без памяти и канала с памятью. Принцип относительной фазовой модуляции. Исключение обратной работы демодулятора.
- •Экзаменационный билет №25
- •1. Импульсная характеристика линейной системы. Свертка сигнала и импульсной характеристики. Формулы свертки для непрерывных и дискретных сигналов. Порядок выполнения дискретной циклической свертки.
- •Экзаменационный билет №26
- •1. Особенности преобразования сигналов в параметрических цепях и системах. Параметрическое преобразование частоты. Принцип работы супергетеродинного приемного устройства. Понятие зеркальной частоты.
- •2. Статистические свойства квадратурных компонент случайного узкополосного сигнала. Статистические свойства огибающей и фазы узкополосного случайного сигнала.
- •Экзаменационный билет №27
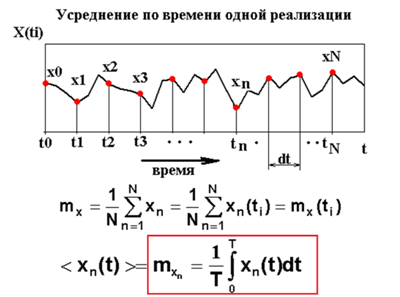
- •1. Усреднение по ансамблю реализаций, усреднение по времени: формулы расчета для дискретных и непрерывных случайных сигналов. Эргодические случайные сигналы.
- •1. Критерий минимального среднего риска.
- •2. Критерий максимального правдоподобия (критерий мп).
- •3. Критерий идеального наблюдателя.
- •4. Критерий Неймана-Пирсона.
- •Экзаменационный билет №28
- •Возможные доп. Вопросы:
- •22 Билет) а нахуя нам каноническая матрица
2. Статистические свойства квадратурных компонент случайного узкополосного сигнала. Статистические свойства огибающей и фазы узкополосного случайного сигнала.
Комплексная огибающая (амплитуда) сигнала -
Огибающую и фазу узкополосного сигнала можно представит следующими выражениями:
Модуль комплексной огибающей является амплитудой действительного узкополосного процесса, а фаза комплексной огибающей совпадает с фазой действительного процесса.
Характерный вид узкополосного процесса:
Экзаменационный билет №27
1. Усреднение по ансамблю реализаций, усреднение по времени: формулы расчета для дискретных и непрерывных случайных сигналов. Эргодические случайные сигналы.
Случайные сигналы описываются случайными функциями, Случайную функцию времени называют случайным процессом. Полная совокупность функций времени представляет собой ансамбль, и будет обозначаться x(ti), где любая функция x t ансамбля есть выборочная функция случайного процесса.
При одном наблюдении случайного процесса получают определенную функциональную зависимость, которую называют реализацией. Условно случайный процесс можно представить в виде совокупности реализаций.
Случайный процесс может быть представлен либо совокупностью (ансамблем) реализаций, либо одной, но достаточно протяженной во времени реализацией.
Стационарный случайный процесс называется эргодическим, если при нахождении его моментных функций усреднение по статистическому ансамблю можно заменить усреднением по времени.
Оно проявляется в том, что каждая реализация случайного процесса достаточной продолжительности несет практически полную информацию о свойствах всего ансамбля реализаций, что позволяет существенно упростить процедуру определения статистических характеристик, заменяя усреднение значений по ансамблю реализаций усреднением значений одной реализации за длительный интервал времени.
2. Статистические критерии оптимального приема.
Количественно помехоустойчивость определяется некоторой мерой соответствия принятого сообщения (сигнала) переданному. Эта мера (мера качества решения) из-за случайного характера помех всегда является статистической и определяется потребителем сообщения (степенью чувствительности потребителя к тем или иным искажениям).
Оптимальный приемник (оптимальное правило решения) обеспечивает наилучшее качество решения, то есть обеспечивает минимум искажений переданного сообщения в соответствии с мерой качества, заданной потребителем. Оптимальное значение меры качества, которое достигается приемником в процессе оптимизации, называется критерием оптимальности приема (или просто критерием качества).
При приеме дискретных сигналов в качестве меры помехоустойчивости обычно используется средний риск Rср, тогда критерием оптимальности является min {Rср};
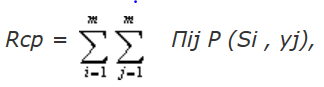 где де
P
(Si , yj)
- совмеcтная вероятность передачи S
i
и приема yj
;
где де
P
(Si , yj)
- совмеcтная вероятность передачи S
i
и приема yj
;
Пij - функция потерь (риск потребителя) при приеме yj , когда передавался сигнал Si ; при этом i = j соответствует правильному приему (значения Пij =0), i ¹ j - ошибка (значения Пij > 0) ;
m - число передаваемых сигналов.
Приемник, работающий по этому критерию, называется байесовским, а правило решения - байесовским правилом.
Рассмотрим некоторые наиболее часто применяемые критерии при передаче двух сигналов S1(t) и S2(t)
При различении сигналов обязательно возникают ошибки при любой мощности сигнала и помехи, так как из-за случайного характера помех возможны выбросы помехи значительной величины.На рис.2.1
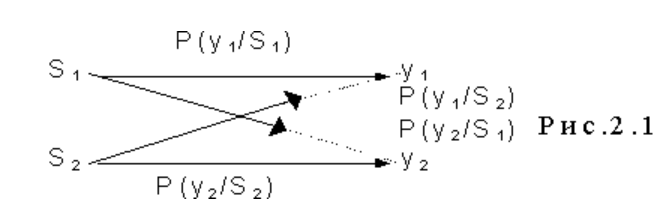
приведен граф переходов в системе связи, когда передаются сигналы S1(t) и S2(t). Если передавался сигнал S1, а принят y1 - это означает, что первый сигнал принят правильно. Если же передавался сигнал S1, а принят у2 - это означает, что при приеме вместо первого сигнала получен второй сигнал - произошла ошибка.
Условные вероятности Р(у1/S1) и Р(у2/S2) есть вероятности правильного приема этих сигналов.
Существует несколько критериев:
