Экзаменационный билет №18

1. Синтез оптимального приемника на согласованных фильтрах. Алгоритм работы и структура оптимального приемника на согласованных фильтрах для бинарных сигналов.

Скалярное произведение (Устройство, непосредственно вычисляющее скалярное произведение (или корреляционный интеграл) (5.27) называют активным фильтром или коррелятором, поэтому приёмник, называют корреляционным.)можно вычислить не только с помощью активного фильтра (коррелятора), описанного в предыдущем параграфе, но и с помощью пассивного линейного фильтра с постоянными параметрами. Если на вход фильтра подать принимаемый сигнал z(t) то напряжение на выходе фильтра в момент времени импульсная характеристика фильтра. Выберем её такой, чтобы в момент t=T получить значение равное скалярному произведению (5.27). Легко видеть, что это будет выполнено при следующем согласовании или

В более общем случае согласованным фильтром для сигнала s(t) называют линейный пассивный фильтр с постоянными параметрами и ИХ:

Где а,t0 постоянные этой ф-ии. g(t) является зеркальным отображением s(t) относительно оси, проведённой через точку t0/2 (рис. 5.7). Для физической реализуемости фильтра необходимо и достаточно, чтобы g(t)=0 при t<0. В частности, для финитного сигнала s(t) поступающего на вход фильтра в момент “t0” и заканчивающегося в момент “T” , условие физической реализуемости согласованного фильтра заведомо выполняется, как видно из рис. 5.7, если постоянная “t0” (момент отсчёта) удовлетворяет условию

Передаточная функция (частотная характеристика) согласованного фильтра с ИХ определяется преобразованием Фурье

+Рис. 5.7 Сигнал s(t) и импульсная характеристика g(t) линейного фильтра, согласованного с этим сигналом

2. Эффективное кодирование источника. Словарное кодирование. Алгоритм Лемпеля-Зива. Порядок составления словаря и порядок формирования кодовых символов для передачи по каналу.

Эффективное кодирование источника - Минимальное среднее количество элементов на выходе кодирующего устройства, соответствующее одному символу дискретного сообщения, можно сделать сколь угодно близким к максимальной энтропии источника.Эффективное кодирование осуществляется с применением неравномерных кодов, в которых более короткие кодовые комбинации соответствуют более вероятным символам сообщения, а более длинные — менее вероятным символам.

Основными требованиями, предъявляемыми к эффективному коду, являются:

• однозначность декодирования, т. е. каждому символу кодируемого сообщения должна соответствовать своя кодовая комбинация и для всех символов комбинации должны быть различны;

• в среднем на один символ сообщения должно приходиться минимальное число элементов кодовой комбинации эффективного кода;

• ни какая более короткая комбинация эффективного кода не должна являться началом другой, более длинной комбинации.

Словарное кодирование - разбиение данных на слова и замена их на индексы в словаре. В настоящее время это наиболее распространенный подход для сжатия данных.

Словарное кодирование, алгоритм Лемпеля – Зива –Велча Процесс сжатия выглядит следующим образом: последовательно считываются символы входного потока и происходит проверка, существует ли в созданной таблице строк такая строка. Если такая строка существует, считывается следующий символ, а если строка не существует, в поток заносится код для предыдущей найденной строки, строка заносится в таблицу, а поиск начинается снова. Для декодирования на вход подается только закодированный текст, поскольку алгоритм LZW может воссоздать соответствующую таблицу преобразования непосредственно по закодированному тексту. Алгоритм генерирует однозначно декодируемый код за счет того, что каждый раз, когда генерируется новый код, новая строка добавляется в таблицу строк. LZW постоянно проверяет, является ли строка уже известной, и, если так, выводит существующий код без генерации нового. Таким образом, каждая строка будет храниться в единственном экземпляре и иметь свой уникальный номер.

Кодирование • Начало. • Шаг 1. Все возможные символы заносятся в словарь. Во входную фразу XX заносится первый символ сообщения. • Шаг 2. Считать очередной символ YY из сообщения. • Шаг 3. Если YY — это символ конца сообщения, то выдать код для XX, иначе: • Если фраза XYXY уже имеется в словаре, то присвоить входной фразе значение XYXY и перейти к Шагу 2 , • Иначе выдать код для входной фразы XX, добавить XYXY в словарь и присвоить входной фразе значение YY. Перейти к Шагу 2. • Конец.

Декодирование • Начало. • Шаг 1. Все возможные символы заносятся в словарь. Во входную фразу XX заносится первый код декодируемого сообщения. • Шаг 2. Считать очередной код YY из сообщения. • Шаг 3. Если YY — это конец сообщения, то выдать символ, соответствующий коду XX, иначе: • Если фразы под кодом XYXY нет в словаре, вывести фразу, соответствующую коду XX, а фразу с кодом XYXY занести в словарь. • Иначе присвоить входной фразе код XYXY и перейти к Шагу 2 . • Конец.

Экзаменационный билет №19

1. Сигнальное созвездие КАМ-16. Алгоритм формирования синфазной и квадратурной компонент в IQ модуляторе. Форма сигналов с модуляцией КАМ 16. Кодирование созвездия КАМ16 по коду Грея.

сигнальное созвездие КАМ-16

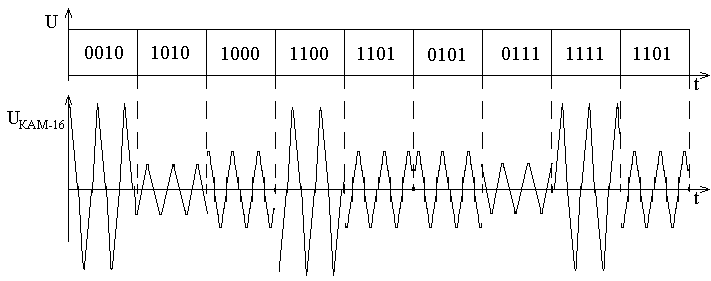
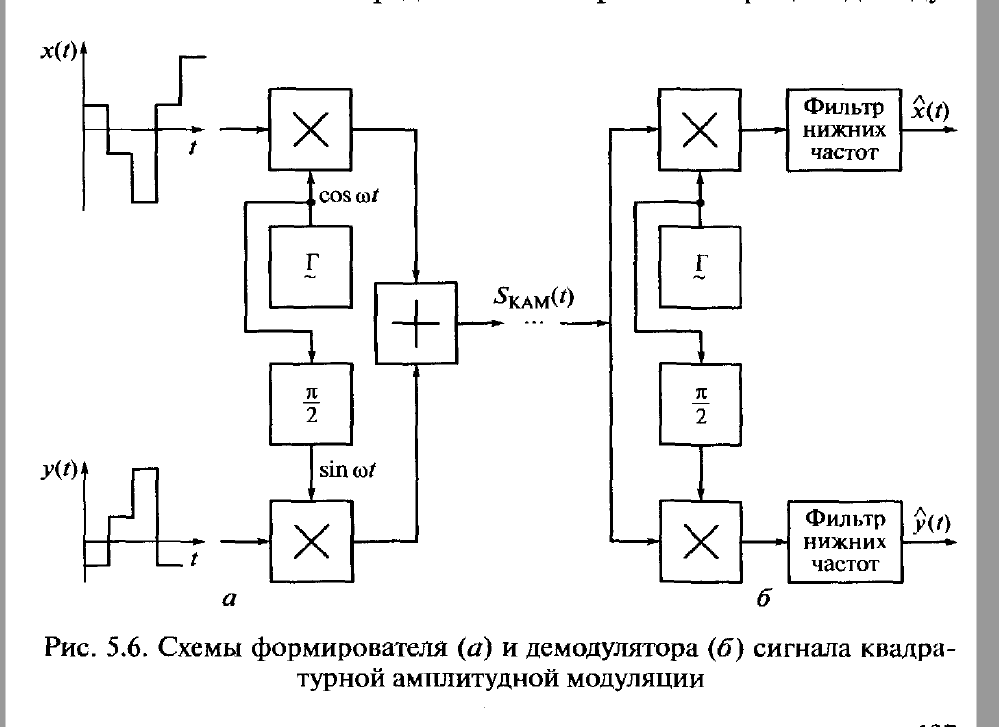
кодирование созвездия КАМ16 по коду Грея.

Наиболее известным и часто применяемым манипуляционным кодом является код Грея, при котором сигнальным точкам, находящихся на минимальном евклидовом расстоянии, ставятся в соответствие кодовые слова, отличающиеся только одним элементом. Существуют коды Грея для КАМ сигналов с при четном . На рис. приведен пример манипуляционного кода Грея для КАМ-16

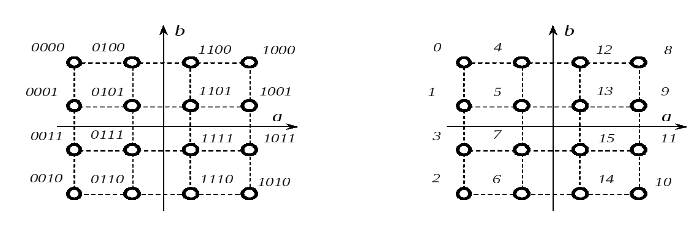
2. Сверточный кодер. Решетчатая диаграмма сверточного кодера. Импульсная характеристика кодера, порядок расчета ИХ и ее путь на решетке кодера.

импульсная характеристика кодера – реакция на единичный символ, подаваемый на вход кодера.

Мы можем описать кодер через его импульсную характеристику, т.е. в виде отклика кодера на единичный проходящий бит.

Последовательность на выходе при единице на входе называется откликом кодера на импульсное возмущение, или его импульсной характеристикой. Для входной последовательности m = 1 0 1 данные на выходе могут быть найдены путем суперпозиции или линейного сложения смещенных во времени входных "импульсов".

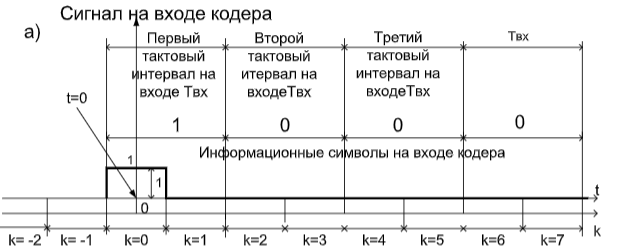
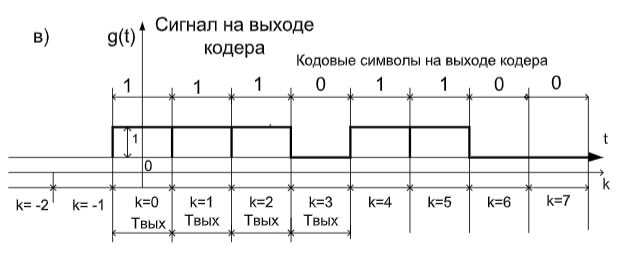
Рис.5 а) Сигнал на входе кодера, изображенного на рис. 1; в) Сигнал на выходе: импульсная характеристика свёрточногокодера.

На рис. 5 введены следующие обозначения:

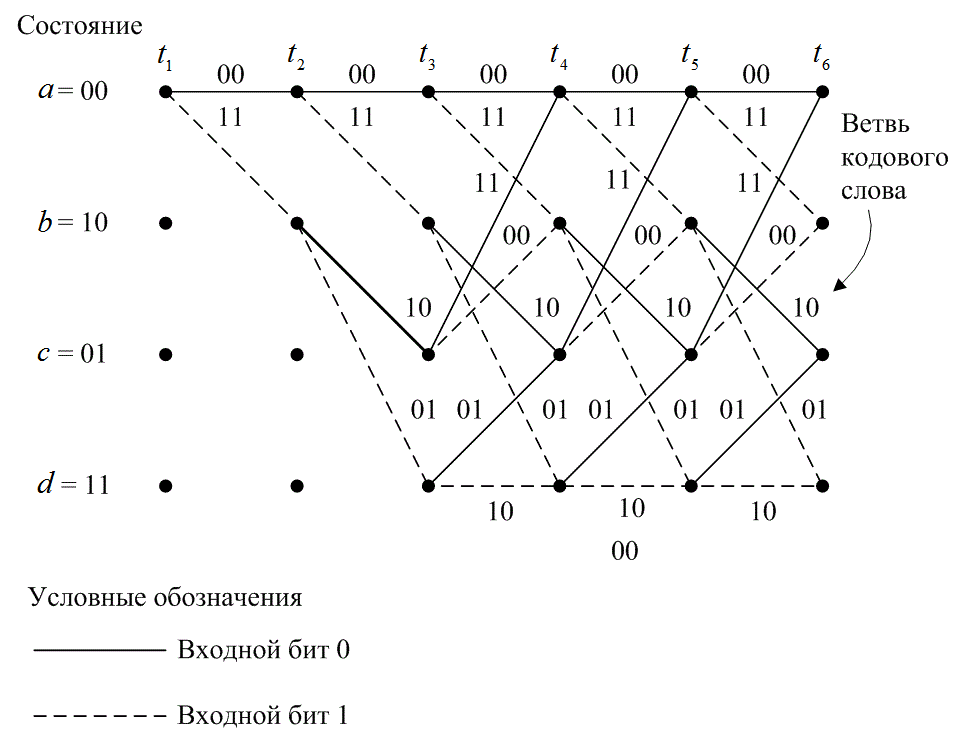
При изображении решетчатой диаграммы мы воспользовались теми же условными обозначениями, что и для диаграммы состояния: сплошная линия обозначает выходные данные, генерируемые входным нулевым битом, а пунктирная — выходные данные, генерируемые входным единичным битом. Узлы решетки представляют состояния кодера; первый ряд узлов соответствует состоянию а = 00, второй и последующие — состояниям a = 00, b = 10, с = 01 и d = 11. В каждый момент времени для представления возможных состояний кодера решетка требует узлов. В нашем примере после достижения глубины решетки, равной трем (в момент времени ), замечаем, что решетка имеет фиксированную периодическую структуру. В общем случае фиксированная структура реализуется после достижения глубины K. Следовательно, с этого момента в каждое состояние можно войти из любого из двух предыдущих состояний.