8.6. Построение теоретической кривой по методу наименьших квадратов

Как правило, в экспериментах задается значение некоторой величины Х и измеряется значение некоторой другой величины У связанной с Х функциональной зависимостью, вид которой не известен. В результате получают таблично заданную функцию . Аналитический вид этой функции неизвестен.

Метод наименьших квадратов (МНК) позволяет построить аналитическое выражение функции (теоретическую кривую) по опытным данным. В соответствии с МНК теоретическая криваядолжна проходить так, чтобы сумма квадратов отклонений ее ординат от экспериментальных данных в опытных точках была минимальной.

Математически эта задача формулируется следующим образом:

(8.6.1.).

Как правило, вид теоретической кривой выбирается в виде полинома

(8.6.2.),

тогда (8.6.1.) записывается так:

(8.6.3.).

В силу квадратичности функционала L относительно коэффициентов и неотрицательности существует единственный минимум. Условия экстремумаL позволяют получить систему m уравнений для вычисления коэффициентов . Эти уравнения называютсясистемой нормальных уравнений:

(8.6.4).

МНК особенно удобен для использования в матричной форме.

Пусть проведен эксперимент в котором получено n пар значений и; теоретическая кривая выбрана в виде полинома (8.6.2).

Введем матрицы:

; ;(8.6.5.).

Система нормальных уравнений размерности будет представлена в виде:

Разрешая это матричное уравнение относительно матрицы , находим:

(8.6.6).

При найденных таким образом коэффициентах условие (8.6.3) выполнится.

Пример 8.6: По МНК построить теоретическую кривую в виде полинома второго порядка для обработки эксперимента:

	1	2	3	4	5	6
	-2	-1	0	1	2	3
	3,3	-0,1	-0,8	-0,5	2,6	9,2

Введем матрицы в соответствии с (8.6.5.):

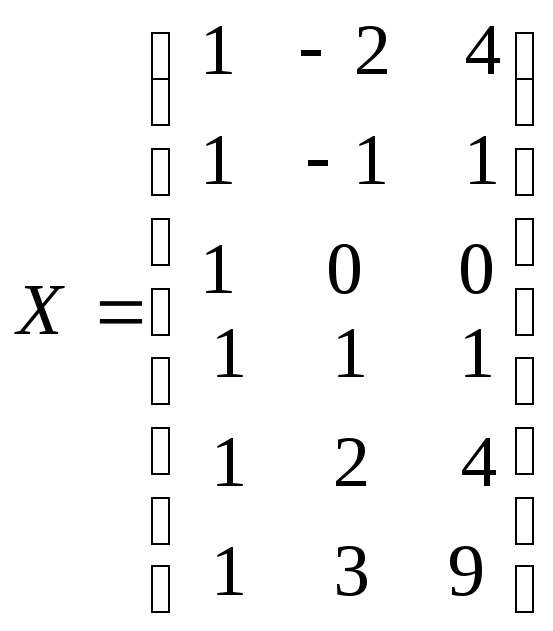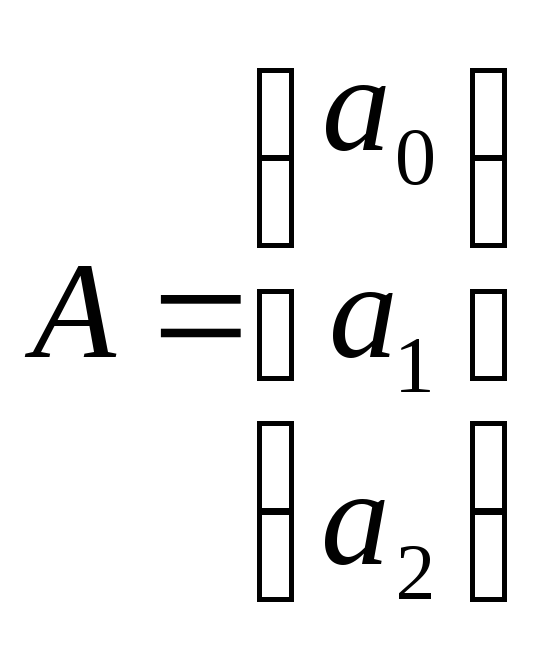; ;; По (8.6.6) находим:.

Теоретическая кривая: .

На рис. 8.4. приведена теоретическая кривая и показаны экспериментальные точки.

Рис. 8.4.

Задачи

8.1. Анализируются статистические данные о продажах в регионах (т. грн.):

123	101	135	122	112	125	127	140	99	101
116	134	123	118	112	119	125	123	143	142
122	142	112	132	99	100	103	100	111	123

Построить простой статистический и вариационный ряды, графические характеристики.

В последующих задачах дано распределение признака Х, полученного по наблюдениям. Необходимо: 1) построить полигон (гистограмму), эмпирическую функцию распределения;

2) найти Точечные оценки выборки: .

8.2 Х – число сделок на фондовой бирже за квартал; n=400 – число инвесторов.

	0	1	2	3	4	5	6	7	8	9	10
	146	97	73	34	23	10	6	3	4	2	3

Ответ:

8.3. Х – месячный доход жителя региона (в грн.); n=1000.

	Менее 50	50-100	100-150	150-200	200-250	Свыше 250
	58	96	239	328	147	132

Ответ:

8.4. Х – удой коров на молочной ферме за лактационный период в ц, n=100 коров.

	4-6	8-10	10-12	12-14	14-16	16-18	18-20	20-22	22-24	24-26
	3	4	11	15	20	14	12	10	6	2

Ответ:

В задачах 8.1 – 8.4 найти доверительные интервалы с надежностью для генерального среднего, дисперсии и среднего квадратического отклонения .

8.5. По данным 9 измерений некоторой величины найдены средняя результатов измерений и выборочная дисперсия. Найти границы, в которых с надежностью 0,99 заключено истинное значение измеряемой величины.

Ответ: .

8.6. Средняя квадратическая ошибка показаний альтиметра (высотомера) самолета равна 15 м. Скольно надо иметь таких приборов на самолете, чтобы с надежностью 0,9 ошибка средней высоты была больше (-30) м, если закон распределения ошибки нормальный?

Ответ: Нужно иметь не менее двух приборов.

8.7. В рекламе утверждается, что месячный доход по акциям А превышает доход по акциям В более чем на 0,3%. В течение годичного периода средний месячный доход по акциям В составил 0,5%, а по акциям А – 0,65%, а его средние квадратические отклонения составили 1, и 2,0%% соответственно. Полагая распределение доходности нормальным, с надежностью 0,95 проверить утверждение, содержащееся в рекламе.

Ответ: Утверждение противоречит имеющимся данным.

8.8 Вступительный экзамен проводился на двух факультетах университета. На первом факультете из абитуриентов выдержали

экзамен , на втором факультете из-. На уровне значимостипроверить гипотезу об отсутствии существенных различий в уровне подготовки абитуриентов.

Ответ: Существенных различий нет. ().

8.9. Расход сырья на единицу продукции составил:

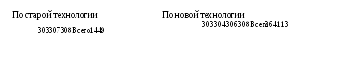
Считая, что расходы сырья по каждой технологии имеет тормальное распределение с одинаковыми дисперсиями, на уровне значимости , выяснить, дает ли новая технология экономию в расходе сырья.

Ответ: Новая технология дает экономию: ().

8.10. Ожидается, что добавление специальных веществ уменьшает жесткость воды. Оценка жесткости проведении до и после добавления веществ по 40 и 50 пробам (%):

до

	3,0 - 3,2	3,2 - 3,4	3,4 – 3,6	3,6 – 3,8	3,8 - 4,0	4,0 - 4,2	4,4 - 4,4
	2	3	4	6	10	9	6

после

	3,0 - 3,2	3,2 - 3,4	3,4 – 3,6	3,6 – 3,8	3,8 - 4,0	4,0 - 4,2	4,4 - 4,4
	3	7	8	10	12	8	2

Подтверждают ли результаты этот эффект?

Ответ: да ()

8.11. По данным задачи 8.10. выдвинуть гипотезу о законе распределения и проверить ее по критерию Пирсона при .

8.12 По данным задачи 8.4. проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности ().

8.13. При 50 подбрасываниях монеты герб выпал 30 раз. Можно ли считать монету симметричной? (решить для ).

Ответ: Монета несимметрична.

8.14. При 120 бросаниях игральной кости шестерка выпала 40 раз. Можно ли считать кость правильной? (решить для ).

Ответ: кость правильная.

8.15. Методом наименьших квадратов построить теоретическую кривую заданного вида ().

	5	10	15	20	25
	59,3	59,8	60,1	64,9	70,2

Ответ:

8.16. Методом наименьших квадратов построить теоретическую кривую заданного вида: ().

	2	4	6	12
	8	5,25	3,5	3,25

Ответ: