8.5.1. Проверка гипотезы о равенстве генеральных средних двух генеральных совокупностей

Проверяется гипотеза :, на уровне значимости. Конкурирующая гипотеза:

Статистика для проверки:

;

критическая область выбирается из условия . Если, то гипотезане отвергается (не противоречит имеющимся наблюдениям).

Пример 8.2. Для проверки эффективности рекламной компании отобраны две группы магазинов. В первой, численностью , где проводилась рекламная компания, выборочная средняя составилапроданных изделий, во второй группе, численностью, где рекламная компания не проводилась, выборочная средняяизделий. Установлено, что дисперсии продаж соответственно равны:. Выяснить: повлияла ли рекламная компания на объем продаж?

 Нулевая гипотеза :, на уровне значимости. Конкурирующая гипотеза:. Фактическое значение критерия (статистики):

.

Критическое значения критерия находится из условия: . Так как, то нулевая гипотеза отвергается, что свидетельствует о влиянии рекламной компании на объем продаж.

8.5.2. Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей. Критерий Фишера-Снедекора.

Пусть имеются две нормально распределенных совокупности, дисперсии которых и. Проверяется гипотеза::.

Конкурирующая гипотеза :.

Статистика для проверки:

;

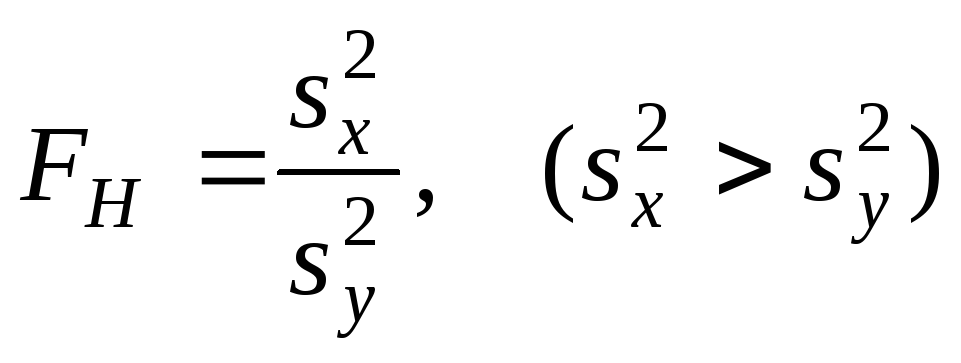Критическое значение критерия Фишера-Снедекора определяется по таблицам: , где- числа степеней свободы дисперсий. Если, то нет основания отвергнуть нулевую дисперсию.

Пример 8,3. Проверяется точность изготовления детали на двух станках x и y. Извлечены выборки объемами иизделий соответственно. При этом рассчитаны исправленные выборочные дисперсиии. На уровне значимостипроверить нулевую гипотезу:при конкурирующей гипотезе:.

 . По таблицам находим:. Так как, то нулевая гипотеза отвергается, т.е. станки не обеспечивают одинаковую точность.

8.5.3. Сравнение выборочной средней с гипотетической генеральной средней нормально распределенной совокупности

а) дисперсия генеральной совокупности известна.

Нулевая гипотеза :.

Конкурирующая гипотеза :;

Статистика для проверки: ;

Критическое значение критерия определяется по таблицам интеграла Лапласа: .

Если , то нулевая гипотеза не отвергается.

Нулевая гипотеза :.

Конкурирующая гипотеза :;

Критическое значение критерия определяется по таблицам интеграла Лапласа: .

Если , то нулевая гипотеза не отвергается.

Нулевая гипотеза :.

Конкурирующая гипотеза :;

Критическое значение критерия определяется по таблицам интеграла Лапласа: .

Если , то нулевая гипотеза не отвергается.

б) дисперсия генеральной совокупности неизвестна.

Нулевая гипотеза :.

Конкурирующая гипотеза :;

Статистика для проверки: , гдеимеет распределение Стьюдента сстепенями свободы дисперсии.

Критическое значение критерия определяется по таблицам двусторонних критических точек распределения Стьюдента .

Если , то нулевая гипотеза не отвергается.

Нулевая гипотеза :.

Конкурирующая гипотеза :;

Критическое значение критерия определяется по таблицам право-сторонних критических точек распределения Стьюдента .

Если, ,то нулевая гипотеза не отвергается.

Нулевая гипотеза :.

Конкурирующая гипотеза :;

Критическое значение критерия определяется по таблицам право-сторонних критических точек распределения Стьюдента , но.

Если, ,то нулевая гипотеза не отвергается.

Для примера 8.1 проверим выполнение гипотезы :при конкурирующей гипотезеи уровне значимости

.

, поэтому нулевую гипотезу следует отвергнуть в пользу конкурирующей и признать, что выработка возросла. 