7.2 Законы распределения функций двух случайных аргументов. Числовые характеристики

Пусть случайная величина Z является функцией двух случайных величин, образующих систему (Х, У), т.е. . Для непрерывной системы (Х,У) с известной плотностью распределения вероятностей , закон распределения Z следует определять, начиная с построения интегральной функции :

, (7.2)

величина z содержится в этом выражении неявно в пределах интегрирования.

Плотность распределения Z можно найти, дифференцируя G(z) по z:

. (7.3)

При известном законе распределения случайной величины Z ее числовые характеристики можно вычислить по обычным правилам, но можно их определить и не прибегая к нахождению закона распределения Z.

Для дискретных Х и Y:

; . (7.4)

Для непрерывных Х и Y:

;

. (7.5)

Пример 7.7. Система (Х₁,Х₂) задана плотностью распределения ; величинаZ есть произведение случайных величин и ; . Найти плотность распределения величиныZ.

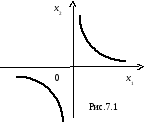
 Графиком функции является гипербола. (Рис. 7.1).

Функция распределения имеет вид:

+.

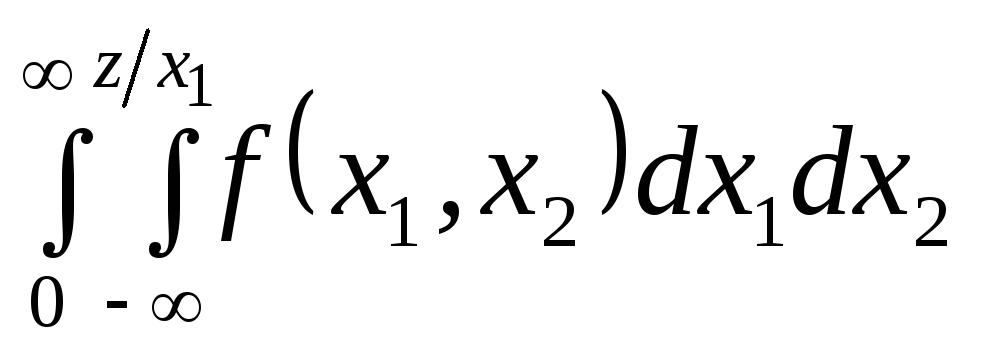Дифференцируя по z, получим:

. 

Пример 7.8. Система (Х,У) задана законом распределения

Х\У	0	1	2	3
-1	0,01	0,06	0,05	0,04
0	0,04	0,24	0,15	0,07
1	0,05	0,10	0,10	0,09

Найти закон распределения случайной величины Z =Х+У.

 Находим значения x_i+y_j: -1, 0, 1, 2, 0, 1,2 , 3, 1, 2, 3, 4. Объединяя одинаковые и располагая их в порядке возрастания, получим возможные значения Z : –1, 0, 1, 2, 3, 4. Вычисляем соответствующие вероятности: ;

; и т.д.

Z	-1	0	1	2	3	4
P	0,01	0,1	0,34	0,29	0,17	0,09

Искомый закон распределения Z имеет вид:

Контроль: 0,01+0,1+0,34+0,29+0,17+0,09=1. 

Пример 7.9. Система (Х,У) задана плотностью распределения , где. Вычислить числовые характеристикиислучайной величины.

 Воспользуемся формулами (7.5)

Получим: =

====,

. 

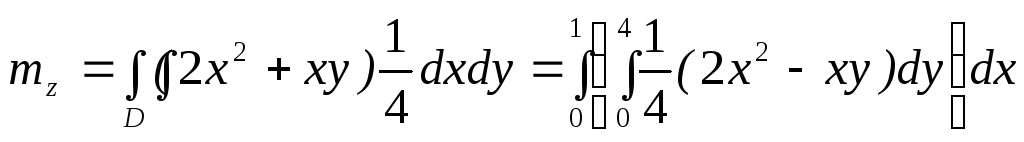Пример 7.10. Система (Х, У) задана законом распределения

Х\У	1	2
0	0,3	0,1
1	0,2	0,4

Вычислить математическое ожидание и дисперсию случайной величины .

 Не определяя закон распределения случайной величины Z, воспользуемся формулами

=

=



7.3. Теоремы о числовых характеристиках и их применение

Процесс вычисления числовых характеристик функций случайных аргументов значительно упрощается, если использовать теоремі о свойствах числовых характеристик, особенно в тех случаях, когда функции – линейны.

Теоремы о математических ожиданиях.

1.

2.

3.

4.

5. Если случайные величины независимы, то

Теоремы о дисперсиях

1.

2.

3. , где - корреляционный момент пары случайных величини.

4.

Пример 7.11. Случайная величина Х – число автомобилей, реализуемых в течение одного дня автомобильным салоном, задана законом распределения

Х	1	2	4	5
Р	0,4	0,3	0,2	0,1

Номинальная стоимость одного автомобиля 3тыс. усл. ед. и за каждый день салон имеет 0,2 тыс. усл. ед. прибыли за счет дополнительных услуг. Указать среднюю выручку, получаемую салоном ежедневно и ее разброс.

 Ежедневная выручка автомобильного салона есть случайная величина , и для решения задачи требуется определитьи. Вначале найдем числовые характеристикиХ:

- в среднем продается 2 автомобиля в день; ,

-разброс продажи составляет 1 автомобиль в день.

На основании теорем о числовых характеристиках будем иметь:

тыс.усл.ден.ед. – средняя ежедневная выручка; тыс.усл.ден.ед. – разброс от средней выручки.

Пример 7.12. Случайная величина Х задана плотностью распределения вероятностей . Найти математическое ожидание и дисперсию случайной величины.

 Функция представляет собой плотность показательного закона распределения, а это значит, чтои. Тогда согласно теоремам о числовых характеристикахи.

Пример 7.13. Случайные величины Х и У, характеризующие соответственно расширение ассортимента выпускаемой продукции и изменение ее качества, заданы своими числовыми характеристиками Вычислить числовые характеристикиислучайной величины, характеризующей колебания прибыли предприятия.

 Согласно теоремам о числовых характеристиках, будем иметь:

; .

Пример 7.14. Плотности распределения вероятностей независимых случайных величин Х и У заданы формулами:

.

Определить математическое ожидание и дисперсию случайной величины .

 Случайная величина Х распределена равномерно в интервале , это значит, чтоСлучайная величина У подчинена показательному закону распределения, следовательно. Так какХ и У независимы, то и согласно теоремам о числовых характеристиках, получим

; .

Задачи

1. Случайная величина Х задана законом распределения

хi	-2	-1	0	1	2
pi	0,1	0,2	0,3	0,3	0,1

Составить закон распределения случайной величины У=X вычислить

Ответ:

Y	0	1	4
P	0,3	0,5	0,2	=1,45

Система (Х,У) задана законом распределения:

Хi\Уi	-2	-1	0
-1	0,1	0,05	0,1
0	0,15	0,1	0,2
1	0,15	0,05	0,1

Найти закон распределения и числовые характеристики случайной величины : а)Z=X+Y; б) Z=XY; в) Z=2X-3Y; г).

Ответ: а) б)

;  =1,07. ;

в) г)

2. Случайная величина Х задана плотностью вероятности . Найти математическое ожиданиеслучайной величины .

Ответ: М=1.

3. Дискретная случайная величина Х задана законом распределения:

Найти функцию распределения F(y), построить ее график и вычислить вероятность события (Y≤4), если .

Ответ: Р(Y≤4)=0,4

4. В партии из 10 деталей содержится 4 нестандартных. Наугад отобраны 2 детали. Записать законы распределения случайных величин Х={число стандартных деталей среди отобранных} и .

Ответ:

Х	0	1	2
Р	2/15	8/15	5/15

У	1/3	1/2	1
Р	5/15	8/15	2/15

,

Случайная величина Х задана плотностью распределения:

.

Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величины .

Ответ:

5. Случайная величина Х задана функцией распределения .Найти плотность распределенияg(y) случайной величины .

Ответ:

6. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Y=sinX, если случайная величина Х задана законом распределения:

xi	-	-/2	0	/2
pi	0,1	0,3	0,4	0,2

Ответ:

7. Партия из 10 деталей содержит 8 стандартных. Наугад отобраны 2 детали. Составить законы распределения случайной величины Х={число стандартных деталей среди двух отобранных} и случайной величины . Определить вероятность того, что Y>4.

Ответ:

Х	0	1	2
Р	1/45	16/45	28/45

У	3	4	5
Р	1/45	16/45	28/45

Р(Y>4)=28/45.

8. Найти математическое ожидание случайной величины Y=e^X, если случайная величина Х задана функцией распределения:

.

Ответ: М= 0,5( е +1 ).

9. Дискретная случайная величина Х имеет возможные значения Х={-2,0,3}. Известно, что математическое ожидание величины Х равно 1.0; а дисперсия равна 1.4. Найти законы распределения случайной величины Х и случайной величины Y=X².

Ответ:

Х	-2	0	3
Р	1/130	85/130	44/130

У	0	3	4
Р	85/130	44/130	1/130

12. Дана плотность вероятности случайной величины: . Найти коэффициента и плотность вероятности случайной величиной Y= e^X .

Ответ: а= 2;

13. Случайная величина Х задана функцией распределения Рэлея: .Найти плотность распределенияслучайной величиныY=e^X.

Ответ:

14. Партия из 5 изделий проверяется на стандартность. Вероятность того, что изделие стандартно, равна 0.8. Определить математическое ожидание и дисперсию случайной величины Х={число стандартных изделий в партии}, а также математическое ожидание и дисперсию случайной величины Y=3X-1.

Ответ:

15. Плотность распределения случайной величины Х: 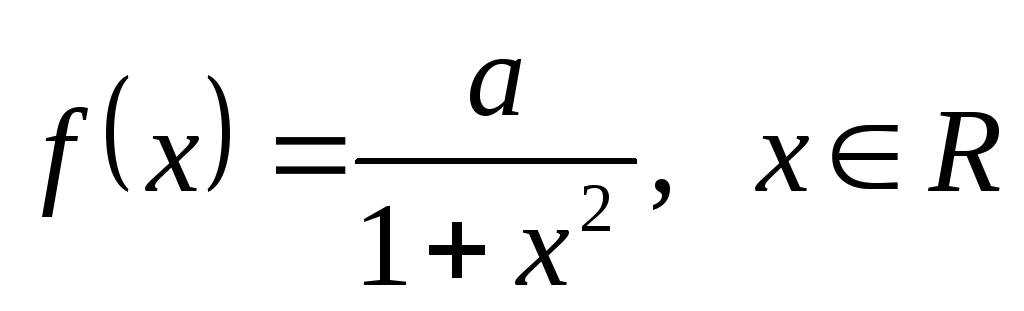. Найти коэффициента и плотность вероятности величины Y=X².

Ответ: а = 1/;

16. Дискретная случайная величина Х задана законом распределения:

xi	-	-/2	0	/2	
pi	0,1	0,3	0,3	0,2	0,1

Вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины =cos X.

Ответ:

16. Задана функция распределения случайной величины Х: . Определить вероятность того, что0.2≤Y≤0.5, если Y=.

Ответ: Р = 0,00195.

16. Случайная величина Х может принимать значения: Х={-1,0,1}. Известно, что математическое ожидание величины Х равно 0, а дисперсия равна 0.08. Составить законы распределения случайных величин Х и Y=X².

Ответ:

Х	-1	0	1
Р	0,2	0,6	0,2

У	0	1
Р	0,6	0,4

16. Случайная величина Х задана рядом распределения:

xi	-1	0	1	2
pi	0,25	0,3	0,2	0,25

Найти функцию распределения F(y), построить ее график и вычислить вероятность события (Y3), если Y=X².

Ответ:

У	0	1	2
Р	0,3	0,45	0,25

.

Р(У3)=Р(У3)=1.

16. Случайная величина Х имеет плотность вероятностей: .

Найти математическое ожидание и дисперсию случайной величины Y=e^X.

Ответ: Му=0,5е;Dy =(e –1)/16.

16. Производится два выстрела с вероятностями попадания в цель при каждом выстреле соответственно 0.6. Составить законы распределений случайной величины Х={ число попаданий при двух выстрелах} и величины Y=2X+2.

Ответ:

Х	0	1	2
Р	0,16	0,48	0,36

У	2	4	6
Р	0,16	0,48	0,36

16. Случайная величина Х имеет плотность распределения вероятностей: . Найти математическое ожидание, дисперсию и среднее квадратичное отклонение величиныY=.

Ответ:

23. Определить математическое ожидание и дисперсию случайной величины Z=4X+Y, если X и Y - независимые нормально распределенные случайные величины с плотностями распределений:

, .

Ответ:

23. Определить математическое ожидание случайной величины Z= XY+X, если X и Y - случайные величины с известными m_x=2, m_y= ‑2 и K_xy= ‑3.

Ответ:

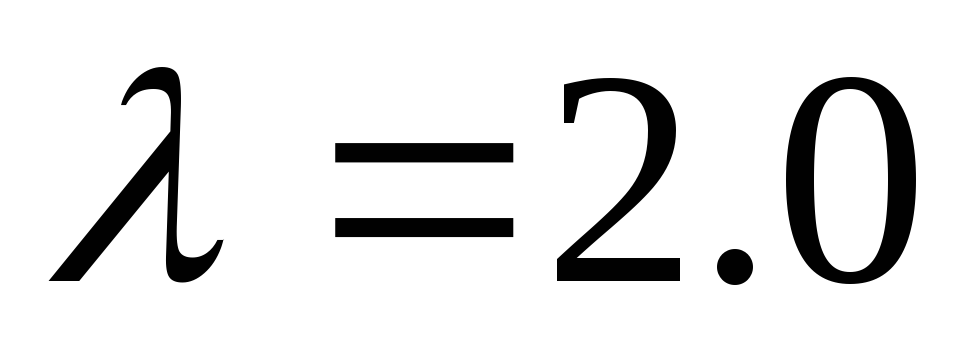23. Заданы две независимые случайные величины X и Y. Величина Х распределена по показательному закону с параметром ; величина Y распределена по тому же закону с параметром . Определить математическое ожидание и дисперсию случайной величины Z=‑3X+2Y.

Ответ:

23. Определить математическое ожидание и дисперсию случайной величины Z=4X-2Y, если X и Y - случайные величины с известными характеристиками m_x=2, m_y=-1, D_x=4, D_y=2, K_xy=2.

Ответ:

27. Случайная величина Х распределена равномерно в интервале . Найти математическое ожидание и дисперсию случайной величины.

Ответ:

27. Случайная величина Х равномерно распределена в интервале (0,3). Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины .

Ответ:

27. Заданы две независимые случайные величины X и Y. Величина Х распределена равномерно на интервале (‑3, 1), величина Y распределена по показательному закону с параметром 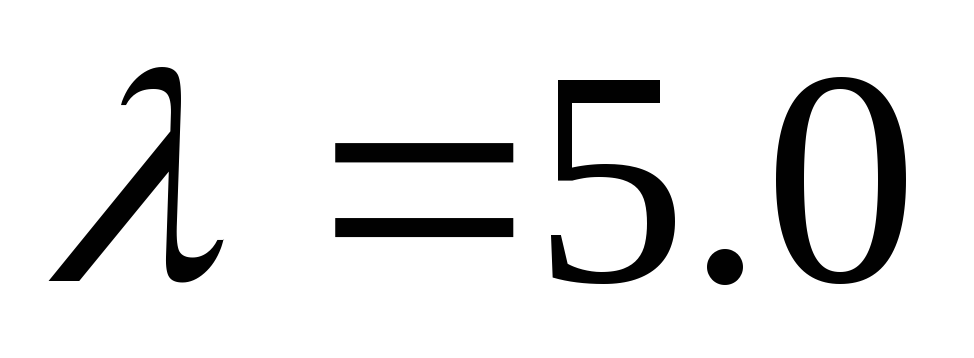. Определить математическое ожидание случайной величины Z= 5XY-3X.

Ответ:

27. Определить математическое ожидание и дисперсию случайной величины Z=3X+4Y, если X и Y - случайные величины с известными характеристиками m_x=‑2, m_y=1, D_x=3, D_y=1, K_xy=4.

Ответ:

27. Определить математическое ожидание и дисперсию случайной величины Z= ‑X+3Y, если X и Y - случайные величины с известными характеристиками m_x= ‑1, m_y=2, D_x=1, D_y=3, K_xy= ‑2

Ответ:

27. Заданы две независимые случайные величины X и Y. Величина Х распределена нормально с плотностью вероятности , величинаY распределена равномерно на интервале (‑5, 1). Определить математическое ожидание случайной величины Z= -2XY-10.

Ответ: