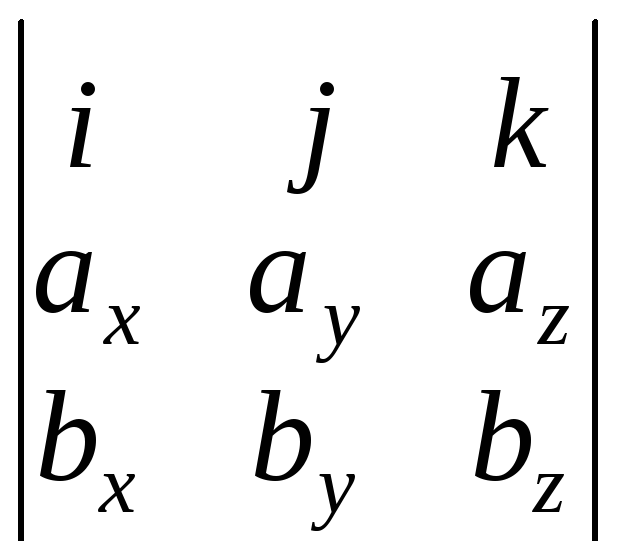Тема 2. Теория

Тема 2. Элементы векторной алгебры. Векторы на плоскости и в трехмерном пространстве. Общие сведения.

 В общем случае вектор представляет собой упорядоченный набор чисел, записанных в строку или столбец. При рассмотрении векторов на плоскости или в трехмерном пространстве принято записывать эти числа в строку и пользоваться геометрической интерпретацией вектора как направленного отрезка, характеризуемого направлением и длиной.

Векторы могут обозначаться как одной буквой, так и двумя прописными буквами. Например: или , где А – начальная точка вектора, В - конечная.

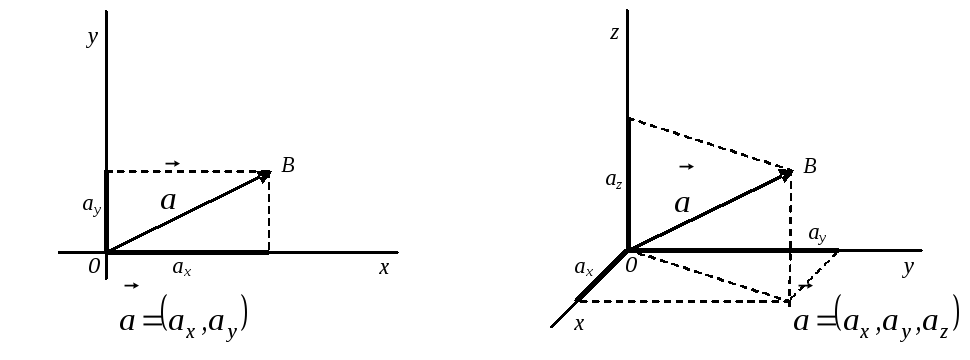Если ввести прямоугольную (декартову) систему координат в плоскости (обозначим как пространство R₂) или трехмерном пространстве (обозначим R₃), то можно говорить о геометрической интерпретации чисел, задающих вектор, как координатах вектора.

Рассматриваются только свободные вектора – их можно перемещать параллельно самим себе. Поэтому, любой из них можно перенести параллельно самому себе так, чтобы его начало совпадало с началом координат. Перпендикулярные проекции вектора на оси координат и будут являться его координатами.

Очевидно, что координаты вектора совпадают с координатами его конца (точка В на рисунке) .

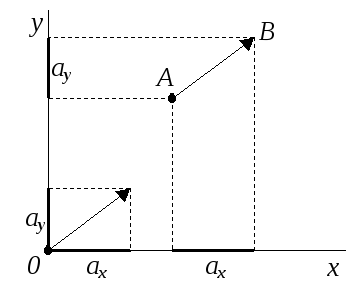Если задать точки начала вектора - т.А (x_A; y_A; z_A), и конец вектора - т.В (x_B; y_B; z_B), то его координаты можно получить, вычитая из соответствующих координат конца вектора координаты начала, т.е.

.

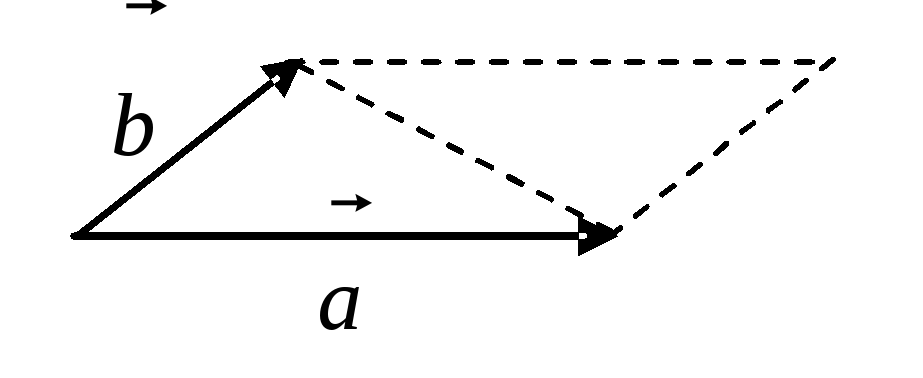
Проиллюстрируем в R₂ правомерность использования свободных векторов. Пусть - некоторый вектор. Очевидно, (см. рисунок) что при его параллельном переносе, например, в начало координат, да и в любую другую точку, его координаты не изменяются.

Нулевой вектор: или .

Противоположный вектор: или .

Операции над векторами в координатной форме как результат действия над их координатами.

• Равенство векторов. Векторы равны, если равны их соответствующие координаты. = → .

• Произведением вектора на число  называется вектор , .

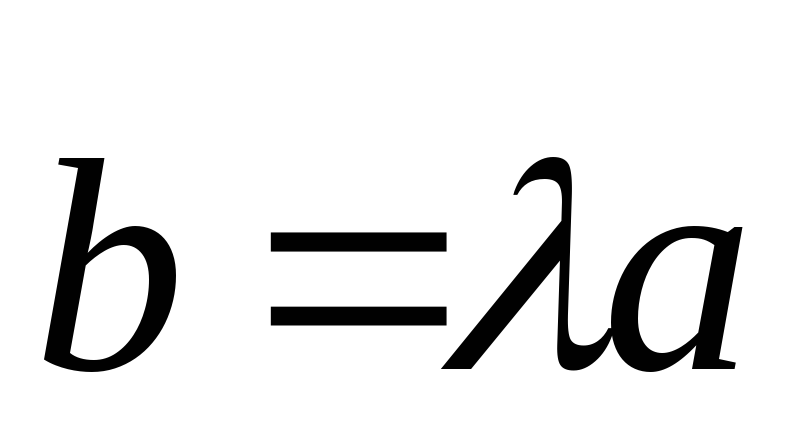• Алгебраической суммой векторов и называется вектор ; .

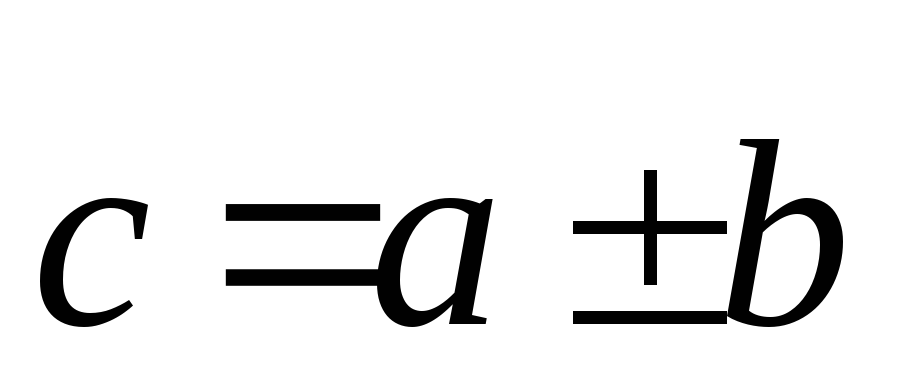 Длина или модуль вектора определяется через его координаты (из геометрических соображений, см. рисунок)

.

 Для любого вектора можно получить его орт. Орт – это вектор единичной длины. Если задан вектор , то его орт будет иметь единичную длину: и совпадать по направлению с вектором .

Е сли Если

- здесь записано действие умножения вектора на число .

Поэтому координаты орта:

Нетрудно убедиться, что при этом . Орты широко используются в векторной алгебре, одно из их применений – указание направления, например, некоторой оси. Для декартовых осей координат введены три специальных орта, обозначаемых: - для ОХ; - для OY; - для OZ. Так как оси перпендикулярны, очевидно, что:

 Разложение вектора по ортам координатных осей – это представление его в виде суммы векторов-составляющих по координатным осям:

Действительно, например, - произведение числа на вектор единичной длины дает вектор - составляющая по оси OZ.

Тогда - по правилу сложения векторов.

Произведения векторов и их свойства

(скалярное, векторное, смешанное).

 Скалярным произведением двух векторов и называется число, равное сумме попарных произведений соответствующих координат этих векторов.

Замечание. Понятие скалярного произведения существует и в пространствах более высокой размерности, чем R₂ или R₃.

Также скалярное произведение может быть выражено формулой

Из нее обычно определяют косинус угла между векторами:

Если ненулевые векторы перпендикулярны, то Поэтому равенство нулю скалярного произведения является необходимым и достаточным условием перпендикулярности двух ненулевых векторов:

Свойства скалярного произведения сходны со свойствами произведения двух чисел:

• 

• 

• .

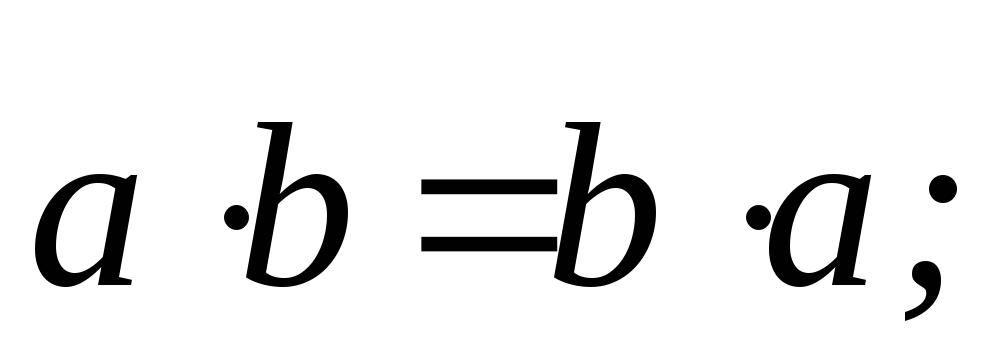
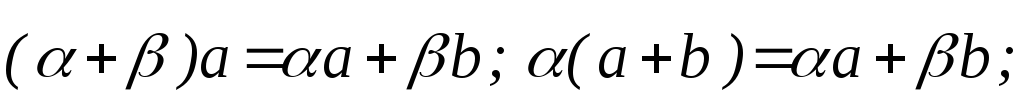
• Векторное произведение двух векторов и 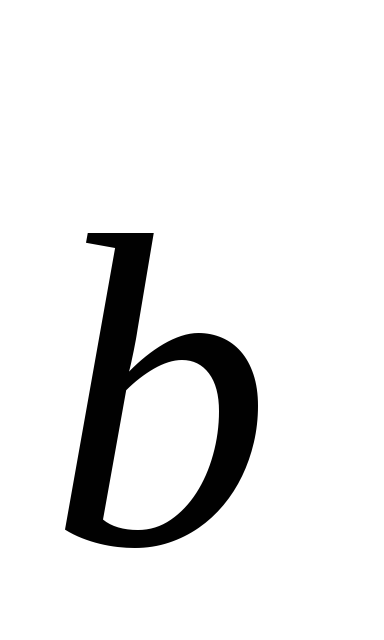- это вектор ,

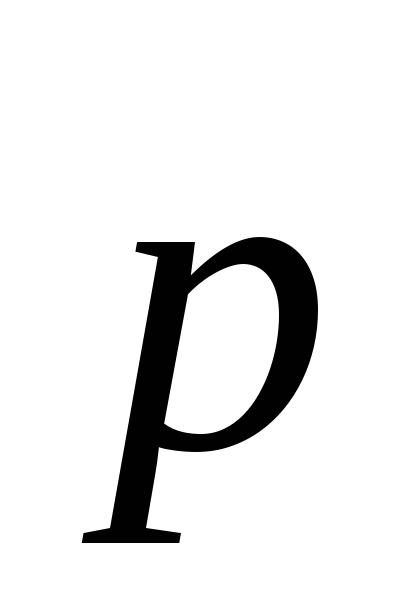• имеющий длину:

• направленный перпендикулярно векторам и , т.е.

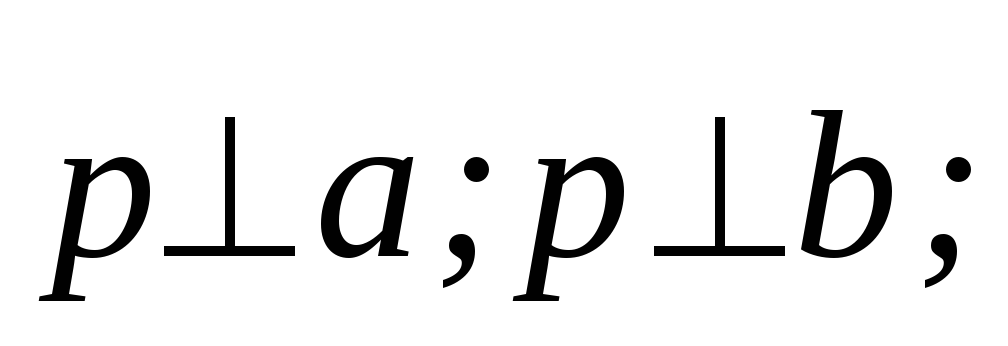
• три вектора , , образуют правую тройку.

Замечание. Направление вектора не будет играть существенной роли в дальнейшем, поэтому определение правой тройки и связанные с этим вопросы можно изучить по литературе [ ].

Если известны координаты векторов и , их векторное произведение можно найти, вычислив векторный определитель:

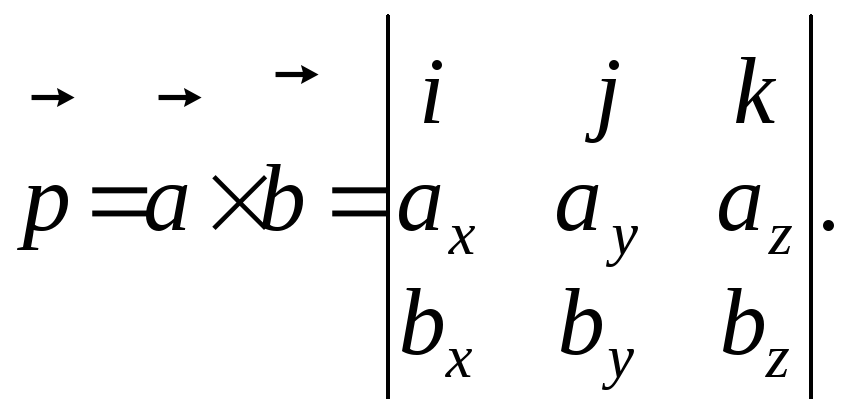
Этот определитель для удобства всегда надо раскрывается по первой строке (см. теорему о разложении определителя по элементам ряда):

При ортах стоят координаты вектора , которые будут получены при вычислении определителей второго порядка.

ПРИМЕР. Найдем векторное произведение заданных векторов:

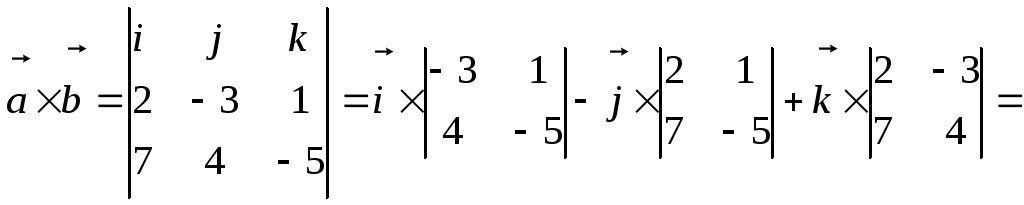
Пиктограмма ?

Если ненулевые векторы коллинеарные (параллельные), то  = 0; sin = 0. Поэтому модуль их векторного произведения . Соответственно, равен нулевому вектору определитель. Из свойств определителя известно, что он равен нулю, если в нем есть пропорциональные ряды. В определителе векторного произведения такими рядами могут быть вторая и третья строки с координатами векторов. Равенство нулю векторного произведения является необходимым и достаточным условием коллинеарности векторов.

или

Свойства векторного произведения:

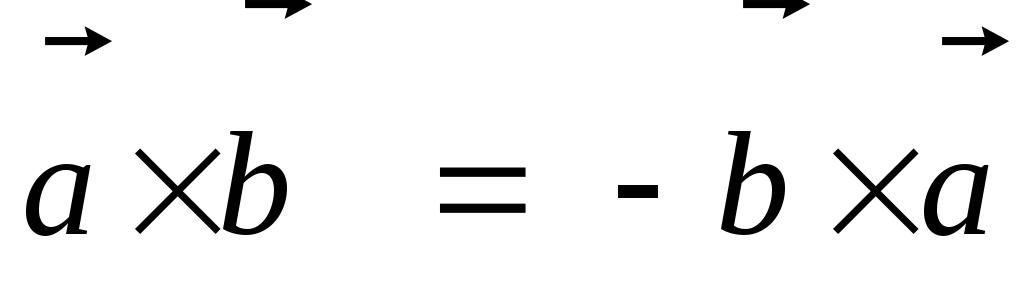• (! антипереместительное);

• остальные свойства подобны свойствам скалярного произведения.

Геометрический смысл векторного произведения: модуль векторного произведения численно равен площади параллелограмма, построенного на векторах-сомножителях. (Показать на рисунке )

,

 Смешанное произведение – определяется для трех векторов и представляет собой число, полученное в результате скалярного произведения векторного произведения двух векторов на третий:

Однако, следуя определению, смешанное произведение вычислять неудобно. Используется формула, определяющая смешанное произведение через координаты векторов:

.

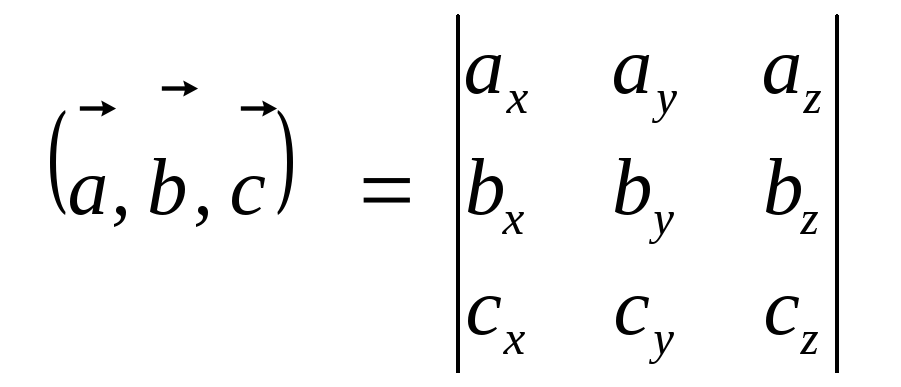Два свободных вектора можно привести параллельным переносом в одну плоскость. Но три и более векторов возможно могут быть приведены к одной плоскости, а возможно нет. Для трех и более векторов вводится понятие компланарности.

• Векторы называются компланарными, если они лежат в одной плоскости, или их можно привести в одну плоскость.

Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения.

.

Геометрический смысл смешанного произведения: модуль смешанного произведения равен объему параллелепипеда, построенного на векторах-сомножителях как на сторонах.

Тетраэдр:

Все, что было сказано о произведениях векторов, можно систематизировать в таблице.

Произведение, обозначение	Результат	Формула для вычисления	Условие равенства 0	Геометрический смысл
Скалярное	число		.	
Векторное	вектор		; .
Смешанное	число		- компланарны

Примечание. В теме 2 векторы рассматриваются заданными своими координатами, как частный случай матриц-векторов. Опущены вопросы, касающиеся физических свойств, не использующиеся в дальнейшем курсе.