
kornil / ФУБ семестр 1 / p71_74
.docТема 3. Теория
Тема 3. Аналитическая геометрия на плоскости
и в пространстве
Начальное понятие аналитической геометрии – понятие точки. Будем считать, что в рассматриваемом пространстве существует прямоугольная система координат. Тогда любая точка будет характеризоваться двумя координатами М(x; y) на плоскости, либо тремя M(x; y; z) в пространстве.
Множества точек могут образовывать линии или поверхности. При этом координаты точек, принадлежащих линии или поверхности, подчинены определенной закономерности, связаны аналитическим выражением, которое называется уравнением линии или поверхности.
F(x;y) = 0 или y=f(x) – уравнение линии;
F(x; y; z)=0 или z=f(x;y) – уравнение поверхности.
Чтобы убедиться, что точка M(a; b) лежит, например, на линии, надо подставить ее координаты в уравнение линии. Если F(a;b)=0, то М принадлежит данной линии, F(a;b)0, то М не принадлежит линии.
Аналитическая геометрия на плоскости.
Виды уравнений прямой линии
Уравнение |
Название |
|
Ax+By+C=0;
|
Общий вид |
|
|
y = k x+b |
С угловым коэффициентом k |
|
|
y - y0 = k (x-x0) |
Пучок прямых, проходящих через т. М(x0,y0) |
|
|
|
Проходящей через две заданные точки M1(x1,y1); M2(x2,y2) |
|
|
|
В отрезках на осях ( a, b – отрезки, отсекаемые прямой соответственно на осях ОХ и OY) |
Угловой коэффициент k – важнейшая характеристика прямой линии. Напомним, что k – это тангенс угла наклона прямой к оси ОХ (на рис. tg). Рассмотрим частные случаи положения прямых на плоскости.
|
Ax+By=0 или y =k x; уравнение прямой, проходящей через начало координат. k – конечное число, 0. При k=1 – биссектриса I-III четверти При k=-1 – биссектриса II-IV четверти. |
|
|
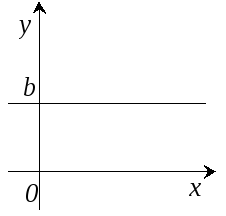
By+C=0 или y=b – уравнение прямой, параллельной оси ОХ (b – любого знака). y = b k = 0. |
|
|
Ax+C=0 или x=a – уравнение прямой, параллельной оси OY (а – любого знака). k; не существует. x = a k .. |
|
|
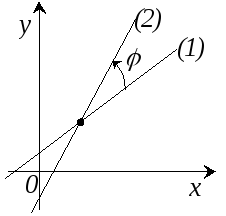
Некоторые задачи аналитической геометрии на плоскости. Угол между двумя прямыми (1) и (2) с угловыми коэффициентами соответственно k1 и k2 определяется по его тангенсу:
|
|
Из этой формулы можно получить условия параллельности () и перпендикулярности () двух прямых.
|
Условие параллельности (). |
Условие перпендикулярности (). |
|
k1 = k2 |
|
|
|
|
Формула для вычисления расстояния от точки M(x0; y0) до прямой, заданной уравнением в общем виде Ax+By+C=0 имеет вид
![]()
Кривые второго порядка
Общее уравнение кривой второго порядка имеет вид алгебраического уравнения 2-й степени:
Ax2+Bxy+Cy2+Dx+Ey+F=0. (*)
На плоскости существует всего три типа кривых второго порядка: эллипс (частный случай – окружность), гипербола и парабола. Для наглядности сведения о кривых представлены в таблице.
Если выполнить операцию выделения полных квадратов по переменным x и y, то заданное уравнение (*)
-
либо приводится к виду, представленному в III колонке таблицы, определяются основные характеристики кривой (центр, полуоси и т.п.) и кривая изображается на чертеже,
-
либо не соответствует ни одному из уравнений кривых второго порядка.
Во второй колонке (II) таблицы приведены уравнения канонически расположенных кривых, центр (для эллипса и гиперболы) или вершина (для параболы) которых совпадает с началом координат. В третьей колонке (III) – уравнения смещенных кривых – это кривые, оси симметрии которых параллельны осям координат, а центр (или вершина) лежит в некоторой точке (x0,y0).
|
I. |
II. |
III. |
IV. |
|
Кривая 2-го порядка |
Каноническое уравнение |
Уравнение смещенной кривой |
Рисунок |
|
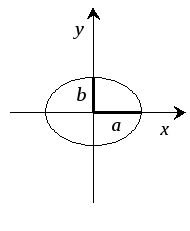
Эллипс |
|
|
|
|
a, b – полуоси эллипса; (x0 , y0) – координаты центра смещенной кривой. |
|||
|
Окружность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
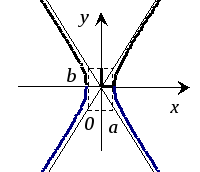
a, b – полуоси гиперболы; (x0, y0) – координаты центра смещенной кривой. |
|||
|
|
|
|
|
|
p – параметр; (x0; y0) – координаты вершины смещенной параболы. Ось симметрии параллельна ОХ. р>0 – ветви вправо, p<0 – ветви влево |
|||
|
|
|
|
|
|
p – параметр; (x0; y0) – координаты вершины смещенной параболы . Ось симметрии параллельна ОY. р>0 – ветви вверх, p<0 – ветви вниз. |
|||
Примеры решения стандартных задач аналитической геометрии в плоскости приведены в разделе "Примеры выполнения обязательного задания по теме 3".





 Гипербола
Гипербола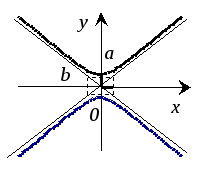 Сопряженная
гипербола
Сопряженная
гипербола Парабола
Парабола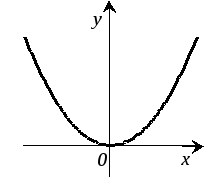 Парабола
Парабола