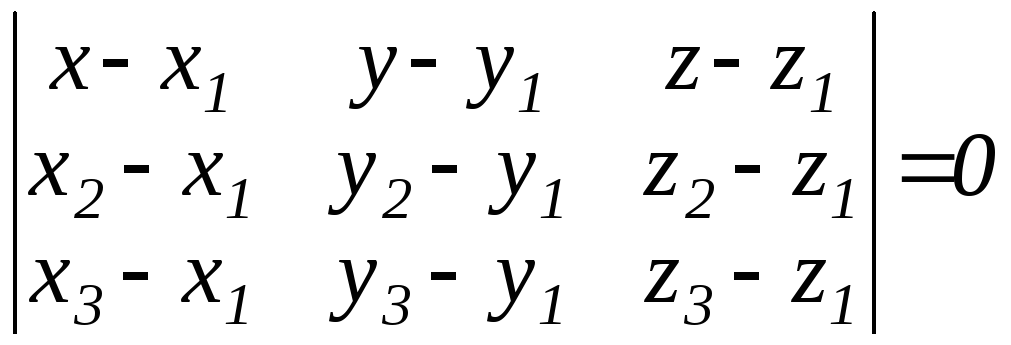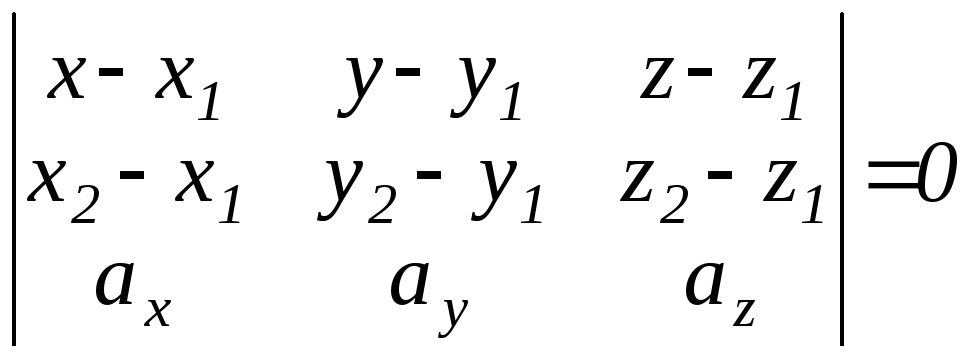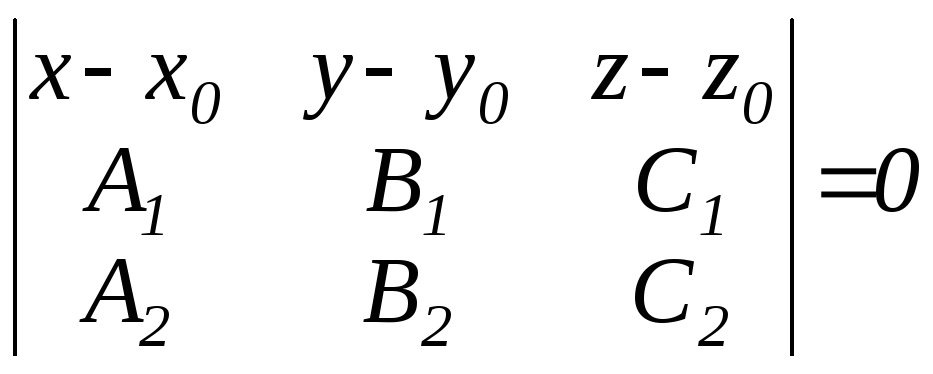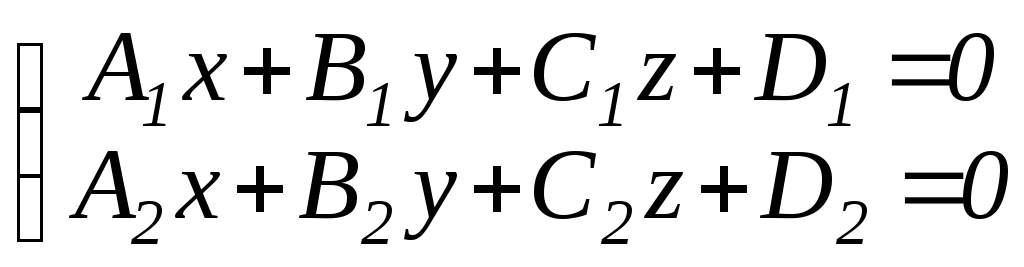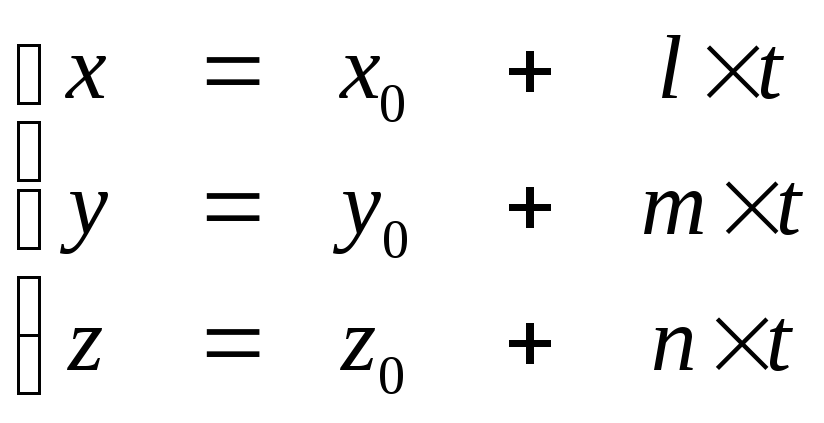Тема 3. Теория

Аналитическая геометрия в пространстве.

Уравнения плоскости и прямой линии.

 Общее уравнение плоскости является алгебраическим уравнением первого порядка относительно координат (x; y; z)

.

- нормаль, вектор, перпендикулярный плоскости.

Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормалей.

Некоторые стандартные виды уравнений плоскости:

1.	Уравнение плоскости, перпендикулярной вектору , проходящей через данную точку М0(х0,y0,z0)	A(x-x0)+B(y-y0)+C(z-z0)=0
2.	Плоскость, проходящая через три заданные точки М1(х1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3)
3.	Параллельная двум заданным векторам и , ( неколлинеарный ), проходящим через точку М0(х0,y0,z0)
4.	Проходящая через две заданные точки М1 и М2, параллельно вектору , ( неколлинеарный )
5.	Проходящая через заданную точку М0(x0,y0,z0), перпендикулярно двум заданным плоскостям: A1x+B1y+C1z+D1=0; A2x+B2y+C2z+D2=0.

Собственно уравнения плоскости будут получены, если раскрыть соответствующий определитель по первой строке.

 Формула для вычисления расстояния от заданной точки М₁(x₁, y₁, z₁) до плоскости, заданной уравнением Ах+By+Cz+D=0:

.

Очевидно, если d=0, то точка М₁ принадлежит плоскости.

 Прямая линия в пространстве определяется как линия пересечения двух не параллельных плоскостей (любых, проходящих через прямую).

Виды уравнений прямой в пространстве:

1		Общие уравнения прямой (пересечение двух плоскостей)
2	, М0(x0, y0, z0) – любая точка, лежащая на прямой. - направляющий вектор прямой	Канонические уравнения прямой или уравнения прямой, проходящей через заданную точку с заданным направляющим вектором
3		Параметрическое уравнение прямой
4		Уравнения прямой, проходящей через две заданные точки М1 и М2

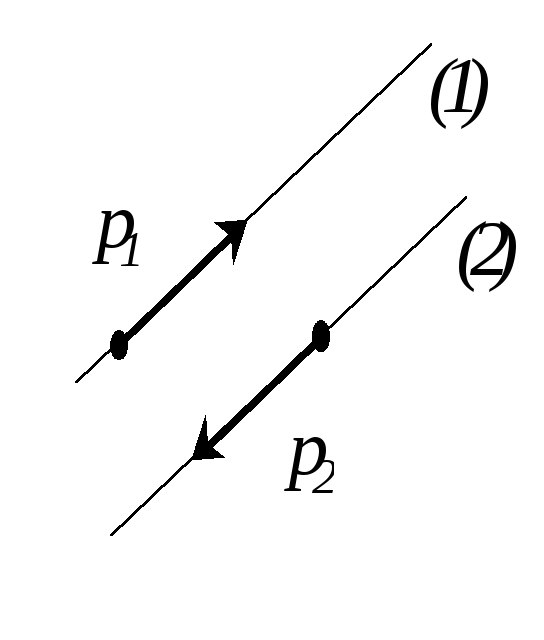
Условия параллельности и перпендикулярности прямых в пространстве определяются как условия соответственно коллинеарности и перпендикулярности их направляющих векторов. Пусть прямые (1) и (2) заданы в каноническом или параметрическом виде, тогда .

	Внимание! Перпендикулярные прямые не обязательно пересекаются. l1l2+m1m2+n1n2=0.

 Условие пересечения двух прямых в пространстве – это условие комплонарности трех векторов:

или

 Переход от общих уравнений прямой к уравнениям в каноническом или параметрическом виде осуществляется следующим образом (возможен и обратный переход).

Заданы уравнения прямой в общем виде: .

Найдем координаты направляющего вектора: 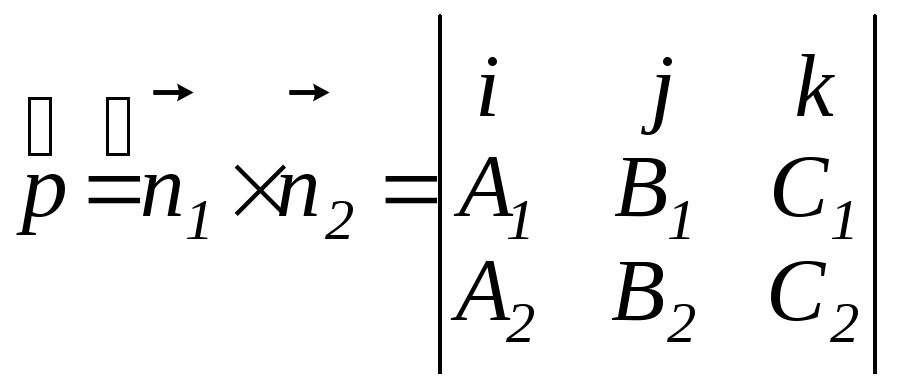как векторное произведение нормалей плоскостей, задающих прямую.

Найдем любую точку, принадлежащую прямой. Она также принадлежит обеим плоскостям, задающим прямую, поэтому ее координаты (x₀, y₀, z₀) можно найти из системы уравнений:

,

в которой одну из координат надо задать произвольно (т.к. находим любую точку), но так, чтобы система имела единственное решение. Координаты вектора и найденной точки подставляют в канонические или параметрические уравнения.

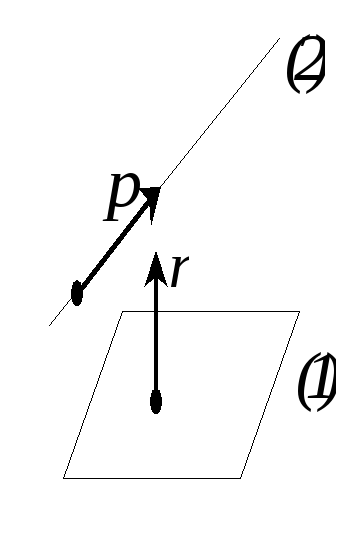
Условия параллельности и перпендикулярности прямой и плоскости формулируют как условия перпендикулярности и параллельности нормали и направляющего вектора.

, Al+Bm+Cn=0.	, .

77