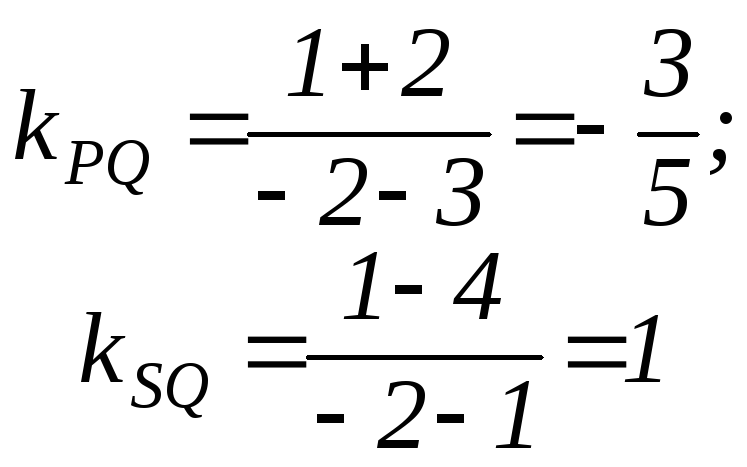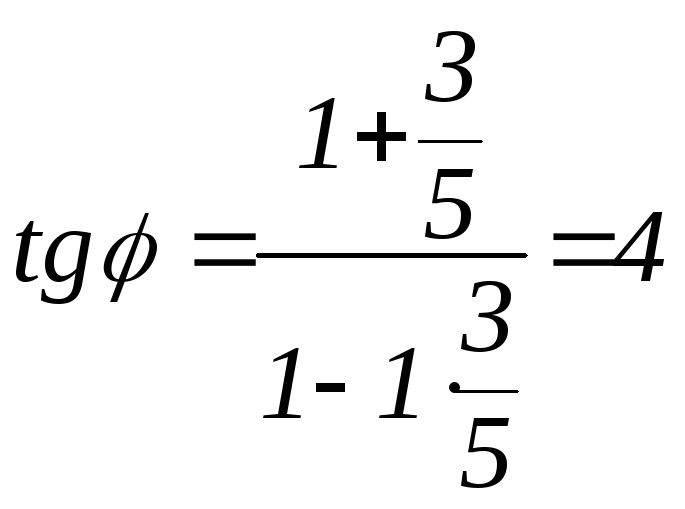kornil / ФУБ семестр 1 / p85_90
.docТема 3. Примеры
Примеры выполнения обязательного задания по теме 3.
Задание 1. Даны координаты вершин треугольника PSQ:
P(3;-2); S(1;4); Q(-2;1).
ПРИМЕР
-
Составим уравнение прямой PS, используя уравнение прямой, проходящей через две точки.
|
Общая формула |
|
|
S(х1,у1); P(х2,у2) |
|
Уравнение прямой PS: 3 х + y - 7=0.
Угловой
коэффициент:
![]() .
.
-
Составим уравнение прямой
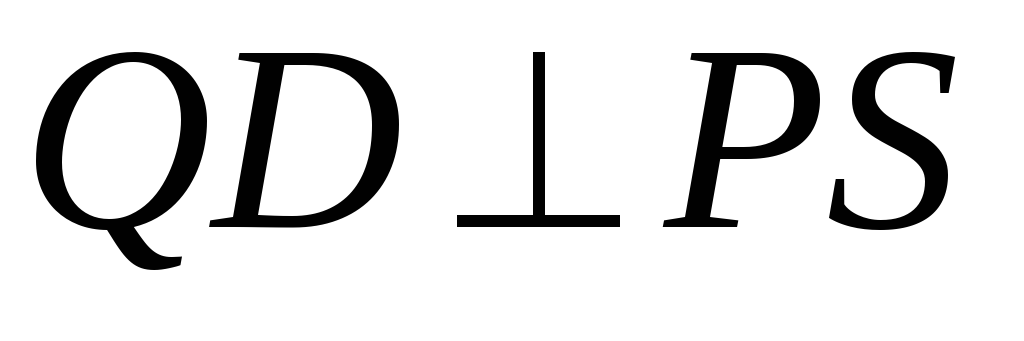 .
.
Из
условия перпендикулярности прямых:
![]() .
.
Составим
уравнение
![]() .
Из условия параллельности:
.
Из условия параллельности:
![]() .
Используем уравнение пучка прямых,
проходящих через точку Q(x0;
y0).
.
Используем уравнение пучка прямых,
проходящих через точку Q(x0;
y0).
|
Общая формула |
|
|
Q(х0 ,у0); k=kQD или k=kQК |
QD:
QK:
|
Уравнение прямой QD QD: x-3y+5=0.
Уравнение прямой QK QK: 3x+y+5=0.
-
Найдем расстояние от точки Q до прямой PS по формуле.
|
Общая формула |
|
|
|
|
.
-
Найдем точку D, как точку пересечения прямых PS и QD , решая систему уравнений
![]() .
.
Для решения системы можно использовать правило Крамера.

-
Найдем тангенс угла между прямыми PQ и SQ.
Угловые коэффициенты прямых, проходящих через две точки:
|
Общая формула |
|
|
|
|
Тангенс угла - между PQ и SQ :
|
Общая формула |
|
|
|
|
-
Ч
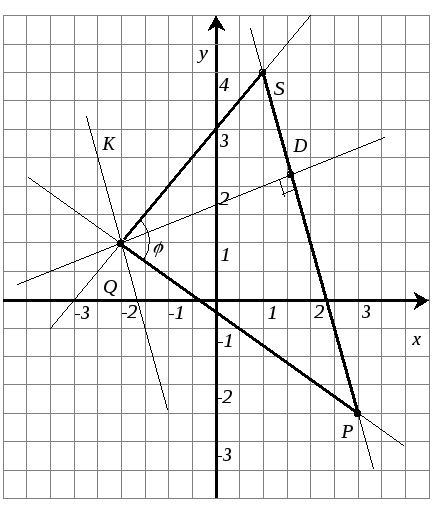 ертеж:
ертеж:
Задание 2. Определить кривые второго порядка и построить их на чертеже.
ПРИМЕРЫ
![]()
Выделим полные квадраты по
переменным х и y:
![]()
![]()
![]()
Уравнение приведено к виду III:
![]() .
.
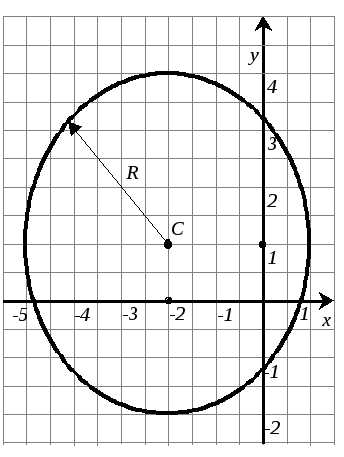
Это уравнение окружности.
Центр окружности: C(x0;y0)=C(-2;1),
радиус
![]()
![]()
Выделяем полные квадраты:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Уравнение
приведено к виду III:
![]() - это уравнение эллипса.
Центр эллипса в точке C(x0;y0)=C(2;-4).
- это уравнение эллипса.
Центр эллипса в точке C(x0;y0)=C(2;-4).
Полуоси:
![]() .
.
Строим прямоугольник со сторонами 2а=12 и 2b=62 так, чтобы центр был в точке С. Затем в прямоугольник вписываем эллипс.

![]() ;
;
Выделяем полные квадраты:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Уравнение
приведено к виду III:
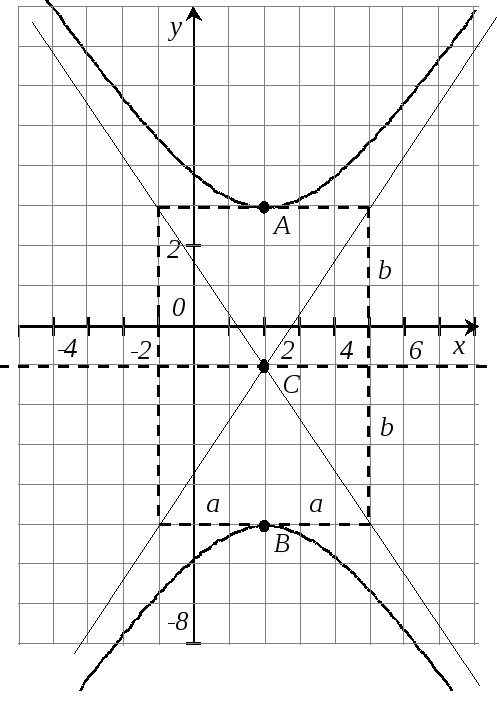
![]() ,
это сопряженная
гипербола.
Ее центр – точка С(x0;y0)=C(2;-1),
полуоси
,
это сопряженная
гипербола.
Ее центр – точка С(x0;y0)=C(2;-1),
полуоси
![]() .
Построение гиперболы начинают с
построения характеристического
прямоугольника со сторонами 2а
и 2b
и центром в точке С.
Затем в этом прямоугольнике проводят
диагонали, выходящие за его рамки,
которые будут асимптотами гиперболы.
Если гипербола обычная, то две ее ветви
будут находится слева и справа от
характеристического прямоугольника,
в углах, образованных его диагоналями.
Если гипербола сопряженная, то ветви
находятся сверху и снизу. Вершины
гиперболы – это точки касания ветвей
и характеристического прямоугольника
(точки А
и В).
.
Построение гиперболы начинают с
построения характеристического
прямоугольника со сторонами 2а
и 2b
и центром в точке С.
Затем в этом прямоугольнике проводят
диагонали, выходящие за его рамки,
которые будут асимптотами гиперболы.
Если гипербола обычная, то две ее ветви
будут находится слева и справа от
характеристического прямоугольника,
в углах, образованных его диагоналями.
Если гипербола сопряженная, то ветви
находятся сверху и снизу. Вершины
гиперболы – это точки касания ветвей
и характеристического прямоугольника
(точки А
и В).

![]()
Выделим полный квадрат для переменной х:
![]()
![]()
![]()
![]()
![]() .
.
Уравнение
приведено в надлежащий вид:
![]() ,
это уравнение параболы.
Для параболы определяем:
,
это уравнение параболы.
Для параболы определяем:
-
координаты вершины:
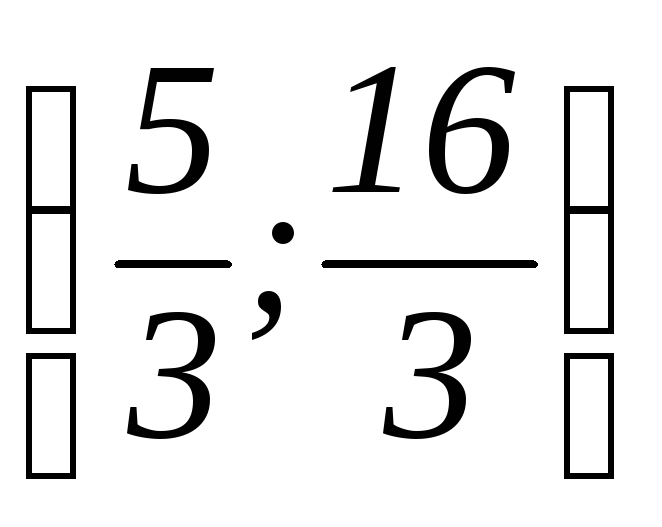 ;
; -
направление ветвей и ось симметрии: ветви направлены вниз, ось симметрии параллельна оси OY,
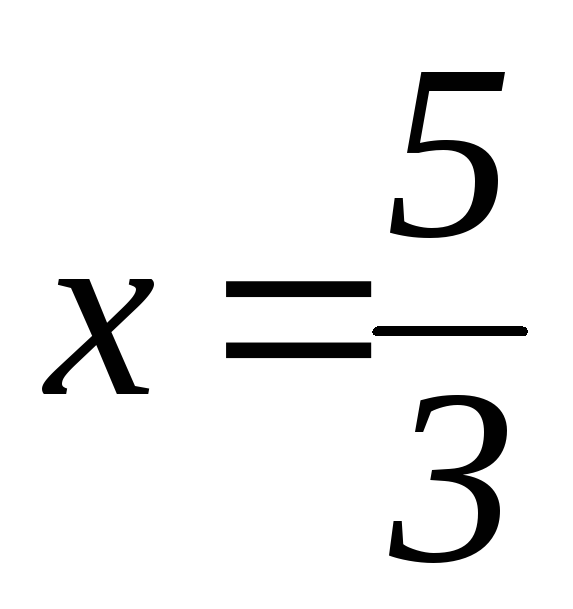 ;
; -
параметр параболы:
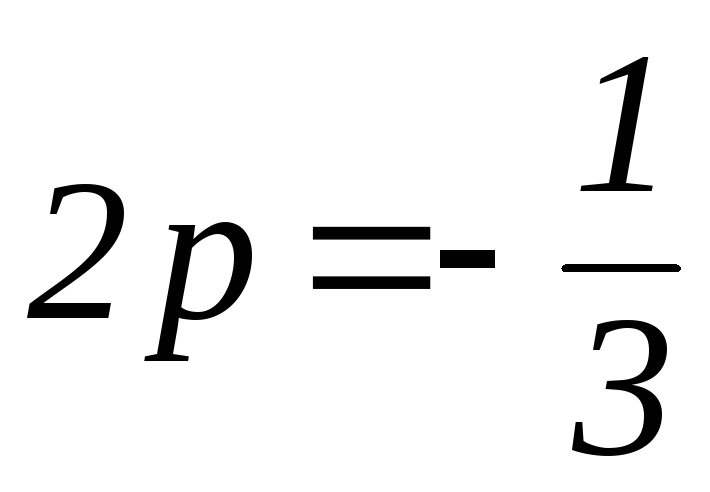 ;
; -
для удобства построения можно определить (приблизительно) точки пересечения параболы с осью ОХ (или OY) y=0; 3x2-10x+3=0; D=64.
 - точки пересечения с осью ОХ,
х=0; y=-3
– точка
пересечения с осью OY.
- точки пересечения с осью ОХ,
х=0; y=-3
– точка
пересечения с осью OY.

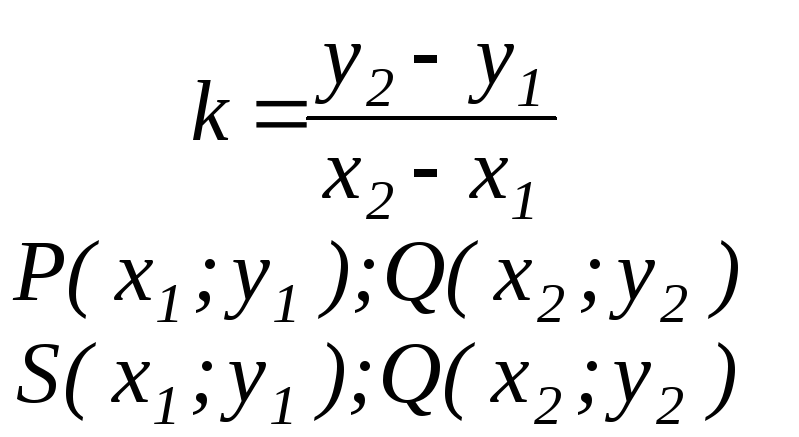 или
или