Тема 1. Теория

Тема 1. Элементы линейной алгебры. Решение систем линейных алгебраических уравнений

Понятие матрицы. Виды матриц

 Прямоугольная таблица чисел, содержащая m строк и n столбцов, называется матрицей. Матрицы обозначаются большими буквами: А, В ,С и т.п.; их элементы обозначаются соответствующими малыми буквами a, b, c и т.п. Каждый элемент матрицы снабжается двумя индексами. Первый индекс означает номер строки, второй – номер столбца, в которых находится данный элемент.

Таким образом, в общем виде матрица:

или кратко: .

Частными случаями матрицы являются:

1. матрица-строка (вектор-строка), матрица-столбец (вектор-столбец): представляют собой матрицы, состоящие из одной строки или столбца. Например:

- вектор-строка;

- вектор-столбец.

Любую матрицу можно рассматривать как набор векторов-строк или столбцов.

или

2. Если все элементы матрицы равны 0, то она называется нулевой и играет роль числа 0 в матричных уравнениях.

3.  Если количество строк матрицы равно количеству столбцов, т.е. m=n, то матрица называется квадратной. У такой матрицы можно выделить главную диагональ, ее составляют элементы с одинаковыми индексами:

.

Побочные диагонали матрицы параллельны главной.

1. Если все элементы квадратной матрицы, кроме диагональных, равны нулю, то матрица называется диагональной:

.

3.2) Среди диагональных матриц выделяют единичную матрицу, на главной диагонали которой стоят единицы. Она играет роль числа 1 в матричных уравнениях:

.

3.3) Квадратная матрица называется треугольной, если ее элементы, находящиеся над или под главной диагональю, равны нулю.

Операции над матрицами

 Операция транспонирования. Эта операция состоит в замене строк матрицы столбцами с соответствующими номерами (или наоборот).

Очевидно, что .

 Равенство матриц. Две матрицы будут равны между собой, если они одинаковых размеров и их соответствующие элементы равны между собой.

если

 Умножение матрицы на число. Чтобы умножить матрицу на число , надо каждый элемент матрицы умножить на это число.

Возможно и обратное действие - вынесение общего множителя всех элементов матрицы.

 Суммирование матриц. Алгебраической суммой двух матриц A_mn и B_mn одинаковых размеров будет матрица C_mn (того же размера), каждый элемент которой равен сумме соответствующих элементов матриц А и В.

Действия  и  обладают теми же свойствами, что и аналогичные операции над числами:

Здесь А,В,С –матрицы, , - числа.

 Умножение матриц. Две матрицы можно перемножить только в том случае, если они обладают согласованными размерами. Согласованность размеров означает, что число столбцов матрицы, стоящей слева, равно числу строк матрицы, стоящей справа.

или геометрически

	n		p		p
m		 n		= m

В результате умножения матриц получается матрица, число строк которой равно числу строк матрицы, стоящей слева, а число столбцов равно числу столбцов матрицы, стоящей справа.

Любой элемент результирующей матрицы можно определить по правилу "строка на столбец":

 Элемент, стоящий в i-той строке и j-том столбце матрицы С получают как сумму попарных произведений элементов i-той строки матрицы, стоящей слева (А), на соответствующие элементы j-того столбца матрицы, стоящей справа (В).

В общем случае операция умножения матриц не обладает переместительным свойством, т.е. АВВА или одно из произведений не существует.

Некоторые свойства произведения согласованных матриц:

ПРИМЕР. Умножить матрицы согласованных размеров. Убедиться, что операция умножения матриц не обладает переместительным свойством.

где

Теперь переставим местами матрицы и найдем . Теперь следует строки брать из матрицы В, а столбцы из матрицы А.

Очевидно, что , это матрицы разных размеров.

Определители, их свойства и вычисление

 Определитель (determinant) – это число, характеризующее квадратную таблицу чисел и вычисляющееся по определенным правилам, через элементы этой таблицы.

Любой квадратной матрице соответствует свой определитель. Например:

Определители обозначаются: D; ; detA; . Обратите внимание на то, что матрица символически записывается в круглых скобках, а определитель – в прямых.

Порядок определителя – это его размер, то есть количество строк (столбцов) в задающей таблице.

 Если detA=0, то матрица называется вырожденной или особенной.

Если detA0, то А – невырожденная или неособенная.

У любого элемента определителя существуют минор и алгебраическое дополнение .

 Минор элемента определителя - это определитель, на порядок ниже исходного, полученный вычеркиванием строки и столбца, в которых стоит элемент .

Например:

 Алгебраическое дополнение элемента a_ij – это минор со знаком по правилу:

Например:

Рассмотрим правила и способы вычисления определителей.

 Правило вычисления определителя 2-го порядка:

Определитель второго порядка равен разности произведений элементов на главной диагонали и на побочной.

 Правило вычисления определителя 3-го порядка можно схематически представить как "правило треугольников".

или в сокращенной записи:

 Для вычисления определителей более высоких порядков применяется метод понижения порядка, который основан на свойствах определителей и на теоремах об определителях.

Рассмотрим свойства определителей, справедливые для определителей любого порядка, на примере определителя второго порядка.

1.Если определитель транспонировать, то его значение не изменится. Из этого свойства следует, что строки и столбцы определителя равноправны. Поэтому в дальнейшем будем называть их рядами.	Действительно,
2. Если поменять местами любые два ряда определителя, то он изменит знак.	Например, поменяем местами столбцы:
3. Определитель равен нулю, если: содержит хотя бы один нулевой ряд; содержит хотя бы два одинаковых ряда; содержит хотя бы два пропорциональных ряда. Пропорциональность рядов означает, что отношение соответствующих элементов таких рядов равна некоторому постоянному числу. Например, пропорциональность строк:	Например, нулевую строку: Например, два одинаковых столбца: Например, две пропорциональных строки:
4. Чтобы умножить определитель на число, достаточно умножить на это число один ряд определителя. Или: Общий множитель элементов любого ряда определителя можно выносить за знак определителя.	Обратите внимание, что это свойство существенно отличается от умножения матрицы на число!
5. Если любой ряд определителя умножить (в уме!) на число к0 и прибавить к параллельному ряду, то определитель не изменится.	Например, умножим на 1-ю строку и прибавим ко 2-ой: = =

 Теорема о разложении определителя по элементам ряда.

Определитель может быть представлен как сумма попарных произведений элементов любого ряда определителя на их алгебраические дополнения.

Например:

Метод понижения порядка использует, в основном, свойство 5 и теорему о разложении. Идея метода: в каком-либо ряду определителя по свойству 5 сделать все нули, кроме одного элемента (обычно это 1), чтобы в разложении определителя по этому ряду осталось одно слагаемое. Пример вычисления определителя методом понижения порядка приведен среди примеров выполнения обязательного задания.

Обратная матрица

 Матрица называется обратной по отношению к квадратной

матрице A, если , где E - единичная матрица.

 Теорема

Для того, чтобы у квадратной матрицы А существовала обратная матрица А^-1, необходимо и достаточно, чтобы определитель матрицы А был не равен нулю, т.е. А была невырожденной матрицей.

Обратная матрица находится по формуле:

где - определитель матрицы А, A_ij — алгебраические дополнения элементов определителя матрицы A. Обратите внимание, что алгебраические дополнения располагаются в транспонированном порядке.

Примеры по вычислению обратной матрицы приведены при решении систем линейных алгебраических уравнений с помощью обратной матрицы среди примеров выполнения обязательного домашнего задания.

Системы линейных алгебраических уравнений (СЛАУ)

В общем случае СЛАУ содержит m уравнений и n неизвестных.

Если выделить матрицу коэффициентов системы ; векторы столбцы неизвестных и правых частей системы:

; , то СЛАУ можно записать в матричном виде:

Если , т.е. , то СЛАУ называется однородной.

При решении СЛАУ могут быть получены следующие варианты:

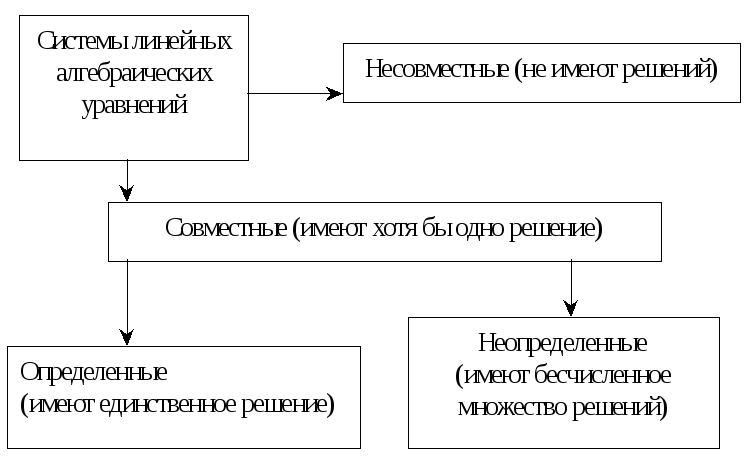
Особенности решения однородных систем ( )представлены следующей схемой:

Решение СЛАУ с невырожденной квадратной матрицей

 1. Правило Крамера.

Здесь матрица системы A_nn – квадратная, следовательно, ей соответствует определитель . Требуется, чтобы матрица была невырожденной, то есть 0. Тогда все неизвестные системы можно найти по правилу Крамера:



где  - главный определитель системы;

– определители, полученные из главного заменой j-го столбца столбцом правых частей .

ПРИМЕР. Решить СЛАУ по правилу Крамера:

Вычислим все определители, которые требуются для решения системы.

Тогда

Ответ:

 2. Решение СЛАУ с помощью обратной матрицы.

Запишем СЛАУ в матричном виде и умножим обе части уравнения на А^-1, обязательно слева:

(слева!)

по определению обратной матрицы, а (умножение на единичную матрицу аналогично умножению на число 1).

Поэтому 

ПРИМЕР. Решить СЛАУ с помощью обратной матрицы.

; здесь ;

Ответ:

13