9. Напряженно-деформированное состояние в точке тела

9.1. Напряженное состояние

Центральным элементом теории напряжений является вектор напряжений р - интенсивность силы действия одной части тела на другую через разделяющую их (мысленно) поверхность. Этот вектор можно проецировать на оси декартовой системы координат, получая матрицу-столбец проекций [р] = [р_х, p_y, р_z]^T (знак «T» означает транспонирование матрицы), или проецировать на нормаль n к площадке и касательную, получая нормальное напряжение σ и касательное τ. Напряженным состоянием в точке тела называют совокупность векторов р на бесчисленном количестве площадок n, которые можно провести через эту точку. Это множество упорядоченно: рассмотрев равновесие произвольного тетраэдра, вырезанного из тела в малой окрестности рассматриваемой точки, легко увидеть, что достаточно знать напряжения на трех площадках, чтобы найти напряжение на любой четвертой. Эти три площадки удобно брать ортогональными (пусть нормали к ним i, j, k направлены вдоль декартовых осей x, у, z), напряжения на них - векторы р_х, p_y, р_z. Из условия равновесия (по силам) получим выражение для напряжения на любой площадке, нормаль которой обозначена п:

, (9.1)

или, в матричной форме,

. (9.2)

Здесь [Т_σ] - матрица напряжений, ее столбцы представляют координаты векторов р_х, p_y, р_z в базисе i, j, k; [п] - матрица косинусов, или координат вектора n в том же базисе. Матрица [Т_σ] однозначно определяет напряженное состояние в точке тела.

Дополнительное условие равновесия по моментам показывает, что матрица [Т_σ] симметрична (парность касательных напряжений).

Пример 1. На рис.9.1 показаны напряжения на гранях кубика (в МПа). Требуется определить нормальное напряжение σ на площадке ABC, равнонаклоненной к двум граням кубика.

Для решения вводим систему координат (х, у, z), формируем матрицы [Т_σ] и [n], находим сначала полное напряжение на площадке ABC (выражение (9.2))

.

Нормальное напряжение находится проецированием вектора полного напряжения на вектор нормали n. В матричной форме это означает перемножение двух матриц

.

Задача. Найдите величину касательного напряжения на этой площадке.

9.2. Круг Мора

Выражение (9.2) удобно для решения задач типа последнего примера, но не наглядно, не позволяет увидеть все множество напряжений в площадках, проходящих через рассматриваемую точку. В значительной мере последнего удается достичь при использовании плоскости {σ, τ}. На этой плоскости откладываются точки [σ, τ], каждая из которых показывает значения нормального и касательного напряжения на некоторой площадке при заданном матрицей [T_σ] напряжённом состоянии. В случае простейшего напряженного состояния - растяжения (сжатия) - легко найти, что пары значений σ и τ для всех площадок образуют на этой плоскости точки, лежащие на одном круге. С ростом угла между осью растяжения и нормалью n к площадке точка [σ, τ] бежит по кругу со скоростью (вокруг центра круга), вдвое большей, чем скорость роста угла.

Следует особо оговорить знак касательных напряжений для данной круговой диаграммы. Правило знаков здесь принимают таким же, как для поперечной силы (на рис. 9.2 касательное напряжение на площадке перпендикулярной оси х равно +50 МПа, на площадке у - равно -50 МПа).

В общем случае картина несколько сложней: точками [σ, τ] на плоскости {σ, τ} охватывается область между тремя касающимися кругами, центры которых лежат на оси σ. Таким образом, на ось σ попадают лишь три точки, отвечающие трем главным площадкам (слово "главный" обозначает отсутствие касательного напряжения на такой площадке). Главные площадки взаимно ортогональны. Главные нормальные напряжения обозначают σ₃, σ₂, σ₁ - в порядке возрастания напряжения, с учетом знака. Каждый круг отвечает площадкам, параллельным одному из главных напряжений.

Отметим, что если все три главные напряжения не равны нулю, то напряженное состояние (НС) называют объемным. Если одно из главных напряжении равно нулю - это плоское НС. При ненулевом значении только одного главного напряжения НС называют линейным.

Пример 2. На рис.9.2 показаны напряжения на трех гранях кубика (в МПа); видно, что площадка с самым большим напряжением - главная. Требуется построить круг напряжений для всех ортогональных ей площадок (в частности, такими площадками являются площадки х и у).

Т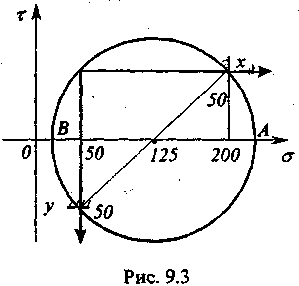очки х и у на рис.9.3 показывают нормальные и касательные напряжения на площадках х и у (в соответствии с рис.9.2); отрезки прямых со штриховкой символи-зируют расположение этих площадок на плоскости {х, у}: х — вертикальная, у - горизонтальная площадка. Угол между площадками равен 90^◦ , значит, центральный угол между точками х и у на круге равен 2·90^° = 180^°. Это однозначно определяет круг Мора и, в частности, два главных напряжения - точки А и В. Величины этих напряжений находят из геометрических соображений; в нашем случае они равны 215 и 35 МПа. Заметим, что величина главного напряжения 10000 МПа (первое главное напряжение) никак не повлияло на полученный круг.

Удобна следующая графическая интерпретация [6]: можно выделить полюс (точка Р на рис.9.4) — на пересечении линий, отвечающим нормалям к показанным площадкам х и у. Если из точки Р провести луч, параллельный нормали к любой другой площадке, то . его пересечение с кругом дает точку, отвечающую напряжениям на этой площадке.

Пример 3. Определить величину и направление главных напряжений для элемента, изображенного на рис.9.5 (напряжения даны в МПа).

Решение. Строим круг Мора для площадок параллельных, оси z (рис.9.6).

Ответ: σ₁ = 95 МПа, σ₂ = 50 МПа, σ₃ = 5,2 МПа, α = 32°. Здесь имеет место объемное напряженное состояние, так как все три главных напряжения отличны от нуля.

Пример 4. Для элемента, изображенного на рис.9.5, найти величину и направление напряжений в площадках, где действуют τ_тах.

Решение. Используя круг Мора, изображенный на рис.9.6, видим что максимальным касательным напряжениям отвечают точки А и . В на круге. В этих площадках действуют τ_тах = 45 МПа, σ_а = 50 МПа, а угол α = 32^◦ + 45^◦ = 77^◦. Соответствующее положение элемента показано слева внизу на рис.9.6.

Пример 5. Пусть задано объемное напряженное состояние: σ₁ = 90 МПа, σ₂ = 30 МПа, σ₃ = - 10 МПа. Требуется определить диапазон изменения касательных напряжений во всех тех площадках, где нормальное напряжение равно σ₂.

Решение. Строим круг Мора (рис.9.7). Рассмотрев треугольник 0₂ВС, наход им, что касательное напряжение по модулю не превышает 49 МПа (что соответствует линии АС из круга Мора).