Методички для олимпийцев / Геометрич хар-ки Теория

1. Геометрические характеристики поперечных сечения брусьев

1.1. Вычисление моментов инерции относительно произвольных осей

1.1.1. Геометрические характеристики поперечных сечений брусьев, вычисленные относительно главных центральных осей, входят в расчетные формулы для определения напряжений и перемещений в брусьях. Без знания этих характеристик невозможно оценить прочность жёсткость и устойчивость брусьев.

Между моментами инерции поперечных сечений относительно центральных осей x₀, y₀, параллельных им осей x, у и наклонённых к последним под углом α осей x₁, y₁ (рис.1.1, а) существуют следующие зависимости:

;

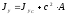; (1.1)

;

;

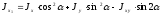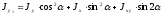(1.2)

Задача 1.1. Определить осевые и центробежные моменты инерции сечения относительно осей x, у ; x₁, y₁ (рис.1.1, в-ж).

Указание. При вычислении J_y в схемах рис.1.1. е, ж сечение разбить на два треугольника (слева и справа от оси у) и воспользоваться решением для нахождения J_y в схеме рис.1.1, д.

1.1.2. Момент инерция плоской фигуры относительно некоторой оси не изменится при сдвиге всей фигуры или отдельных её частей параллельно данной оси. Доказательство этого положения следует из определения осевого момента инерции (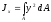) и рис.1.2, а.

Задача 1.2. Вычислить момент инерции сечения относительно оси x (рис.1.2, б-е) рациональным способом.

1.1.3. В некоторых случаях при определении момента инерции удобно достроить заданное сечение до такой фигуры, для которой величина осевого момента инерции известна (рис.1.3, а). Из рис. 1.3, а очевидно:

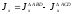
Задача 1.3. Для сечений, указанных на рис.1.3, б-г, вычислить момент инерции относительно оси x.

Указание. Дополнить сечения на рис.1.3, б-г соответственно до параллелограмма, двух квадратов, кольца.

1.2. Главные оси и главные моменты инерции сечения

1.2.1. В теории геометрических характеристик широко используются формулы для определения направления главных осей и вычисления главных моментов инерции по известным осевым и центробежному моментам инерции относительно произвольных исходных осей х, у (рис.1.1, б):

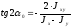, (1.3, а)

. (1.3, б)

Задача 1.4, Для сечений на рис.1.1, в-е найти положение главных осей инерции, проходящих через точку А, и величину главных моментов инерции.

Указание. Моменты инерции относительно осей х, у ( J_x, J_у, J_xу ) взять из задачи 1.1.

1.2.2. Основной признак главных осей - равенство пулю центробежного момента инерции относительно этих осой:

J_uv = 0. (1.4)

На использовании условия (1.4) основаны способы отыскания главных осей инерция без определения угла α₀ по формуле (1.3, a).

Если сечение состоит из двух одинаковых фигур, расположенных под углом 90˚, то одна главная центральная ось проходит через центры тяжести обеих фигур, а другая – перпендикулярно ей через центр тяжести сечения С (рис.I.5, а)..

Задача 1.5. Указать положение главных центральных осей инерции и ту из них в каждом сечении (рис.1.5, б-г), относительно которой осевой момент инерции минимален.

Теорема. Если сечение имеет ось симметрии, то она, и любая ось, перпендикулярная ей, являются главными осями инерции. Доказательство данного утверждения очевидно из рис.1.6, а.

Задача 1.6. Не проводя вычислений, найти положение главных осей, проходящих через точку О плоской фигуры (рис.1.6, б-з).

Указание. Сечение разбить на две фигуры и в первой провести ось симметрии, которая перпендикулярна оси симметрии второй фигуры. Тогда 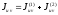= 0.

Задача 1.7. Для заданных сечений (рис.1.7, а-г) определить разность моментов инерции относительно главных осей, проходящих через точку О.

Указание. Положение главных осей, проходящих через точку О - смотри решение задачи 1.6.

1.2.3. Если сечение имеет более двух осей симметрии (рис. 1.8, а), то все центральные оси являются главными и моменты инерции относительно их будут равны. Доказательство теоремы легко получить из формулы (1.2), если принять, например, что оси y, y₁ - неперпендикулярные оси симметрии, т.е. главные центральные оси сечения, и потому = 0 ( у ┴ х, у₁ ┴ х₁ ). При этом из выражения для 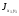имеем J_x = J_у. Учитывая последнее равенство в выражениях (1.2), убеждаемся, что при любом α центробежный момент инерции равен 0, а осевой момент инерции - постоянен.

Задача 1.8. Определить осевые и центробежный моменты инерция плоской фигуры относительно осей у₁, х₁ (рис. 1.8, б-г).

1.2.4. Если главные моменты инерции относительно двух осей, проходящих через некоторую точку сечения, равны, то все оси, проведенные через эту точку, являются главными и моменты инерции относительно их равны. Доказательство теоремы читатель легко получит из выражений (1.2), полагая, что оси х, у - главные и J_x = J_у.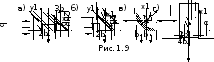

Задача 1.9: Найти момент инерции сечения (рис.1.9) относительно оси x₁.

Задача 1.10. Для плоских сечений (рис.1.10) найти точки, обладающие таким свойством, что все проходящие через них оси являются главными. Оси х, у принять центральными. (для рис.I.10, г считать известными величины J_x, J_у, J_xy). Дополнительно исследовать последний случай (рис.1.10, г), когда J_xy = 0.

Указание. Через искомую точку 0 провести главные оси u, v, параллельные исходным осям х, у. По формулам (I.I) записать выражения для J_и, J_v, J_uv. Координаты искомых точек (а; с) определяются из двух условий: J_uv = 0 и J_u = J_v.

1.2.5. Если относительно произвольных ортогональных осей моменты инерции равны, то главные оси проходят через начало координат под углом 45° к исходным осям. Доказательство очевидно из формулы (1.3, а).

Задача 1.11. а) Для сечений, указанных на рис.1.11, а-в определить на оси x положение точек, через которые главные оси проходят под углом 45° к исходной оси x.

б) Для прямоугольника (рис.1.11, а) найти точки, через которые главные оси проходят под углом 45° к его сторонам, если разность моментов инерции относительно главных осей равна .

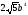в) Определить, при каком n максимальный момент инерции относительно оси, проходящей через точку 0 (рис.1.11. г), вычисляется по формуле J_v = J_x +│J_xy│.

г) В равнобедренном треугольнике (рис.1.11, д) определить высоту и разность моментов инерции относительно главных осей u, v, расположенных под углом 45°к осям х, у.

Указание. При решении задач воспользоваться формулами (1.3, а), и (1.3, б).

1.3 Определение осевых моментов инерции сечений, имеющих центральную симметрию

1.3.1. Если сечение имеет центральную симметрию и бесконечное количество главных центральных осей, то удобнее сначала вычислить полярный, а потом, осевые моменты инерции сечения.

Задача 1.12. Определить осевые моменты сопротивления Wx и Wy данной плоской фигуры (рис.1.12).

РЕШЕНИЕ

Сечение имеет более двух осей симметрии, следовательно, все центральные оси будут главными и Обозначим полярные моменты инерции сегмента, круга и квадрата соответственно: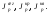

Очевидно, что для каждого сегмента (рис.1.12 Р, а) 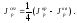Учитывая, что осевые моменты инерции квадрата имеем

Тогда очевидно, что полярный момент заданной фигуры равен

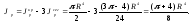
Тогда

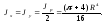
Окончательно имеем:

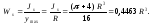
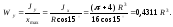
1.4. Определение экстремальных значений осевых моментов инерции и моментов сопротивления

Если какой-либо параметр сечения является переменным, то записывается выражение для J_x (W_x), в которое входит этот параметр, и затем полученное выражение исследуется на экстремум.

Задача 1.13. а) Для заданных сечений (рис.1.12, а-е) определить значение α, при котором осевой момент сопротивле-ния максимален.

б) Для схем на рис.1.13, в-д найти, при каком α осевой момент инерции относительно центральной оси имеет наибольшую величину.