5.7. Определение перемещений

При определении перемещений в статически неопределимой задаче, как и в статически определимой, рационально использовать метод Мора: формулировать вспомогательную задачу, удалив все внешние воздействия на конструкцию и приложив фиктивную единичную нагрузку требуемого типа. Подчеркнем, что конструкция (вместе с опорами) во вспомогательной задаче должна быть прежней, то есть вспомогательная задача также статически неопределима.

Однако анализ показывает, что второй раз раскрывать статическую неопределимость (при фиктивной нагрузке) не нужно. Это связано с тем, что величины X_i характеризуют самoуравновешенное состояние внутренних сил, а деформации в конструкции всегда совместны (речь идет о полных деформациях, а не о монтажных, или тепловых, или силовых составляющих деформации). Работа же самоуравновешенных сил на совместных деформациях всегда равна нулю - независимо от величин X_i.

Рассмотрим, например, случай один раз статически неопределимой конструкции. Во вспомогательной задаче для внутренних силовых факторов и для реакций опор (смещающихся или не смещающихся, но мешающих) справедлива суперпозиция:

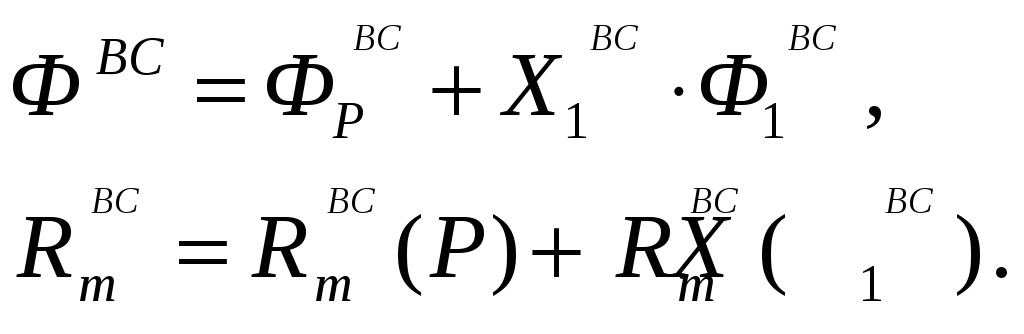
После подстановки этих выражений для внешних и внутренних сил в определение Мора для перемещения при наличии смещающихся опор (2.5) получим

(учтено, что при отсутствии фиктивной нагрузки во вспомогательной задаче реакции отброшенных связей пропорциональны параметру ). Однако выражение в последней скобке равно нулю - в связи с требованием совместности (5.5) для деформации Д(z) в основной задаче. Таким образом, при вычислении перемещения определять значение нет необходимости, оно все равно будет умножено на ноль. Можно записать

, (5.11)

(что соответствует приравниванию нулю), но бывает удобно, не раскрывая второй раз статическую неопределимость, принять для этой неизвестной какое-нибудь другое значение и использовать выражение (2.5).

Пример 7. Рама на рис.5.20 выполнена идеально (Д° = 0), но крепится на опоры, изготовленные неточно. Насколько сместится точка А по сравнению с чертежом?

Решение. Первая часть задачи - определение упругих деформаций (построение эпюры изгибающих моментов) решается стандартно. Поскольку предполагается, что смещаются все опоры, в основной системе придется снять все внешние связи. Появятся три обычные степени свободы (рис.5.21, неизвестных четыре, степень статической неопределимости равна единице). Каноническое уравнение имеет вид (смешения считаются положительными, если их направления отвечают стрелкам на рис.5.21). Полученная после раскрытия статической неопределимости эпюра кривизн показана на рис.5.22, где обозначено . Для определения положения точки А следует найти ее горизонтальное и вертикальное смещение, вызванное смещениями опор Д. Очевидно, что горизонтальное смещение равно Δ₄ (продольной деформацией стержня, как обычно, пренебрегаем по сравнению с изгибной).

Ч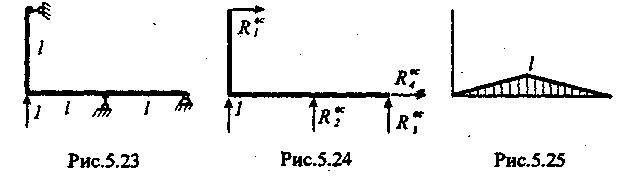тобы найти вертикальное перемещение v, следует решить вспомогательную задачу: приложить в точке А вертикальную единичную силу (рис.5.23, ищем перемещение вверх). Для решения нам понадобятся изгибающие моменты и все опорные реакции во вспомогательной задаче (рисунок 5.24 - эквивалентная система во вспомогательной задаче). Поскольку значение неизвестной нам не важно, можно выбрать любое из бесконечного множества решений системы уравнений равновесия во вспомогательной задаче, то есть она как бы превращается в статически определимую. Покажем это, выбрав два варианта решения вспомогательной задачи.

Решение а. Примем значение на рис.5.24 равным нулю, тогда = - 2, = 1, = 0. Эпюра изгибающих моментов во вспомогательной задаче в этом случае показана на рис.5.25;

.

Как видим, результат не зависит от жесткости рамы, если последняя постоянна.

Решение б. Если приравнять нулю не , a, то получим = - 1, = 1, = 1. Эпюра М^BC показана на рис.5.26, из выражения (2.5) получаем 1

Ответ тот же.

В приведенных вариантах «решения» вспомогательной задачи мы приравнивали одну из реакций нулю чтобы получить попроще эпюру изгибающих моментов. Можете для упражнения приравнять одну из реакций, например, 13,5. Если правильно найдете остальные и не ошибетесь при построении эпюры М^BC, получите прежний ответ.

Пример 8. В ферме, показанной на рис.5.27, пары обозначенных стержней одинаковы, их длины равны l и ·l). Требуется найти угол поворота стержня 1.

Решение. Задача кососимметрична; это нетрудно увидеть, сместив точку приложения силы Р к центру абсолютно жесткого горизонтального стержня (рис.5.28). По рекомендации для ферм, при построении эквивалентной системы разрезаем все стержни и обозначаем неизвестные реакции снятых связей с учетом косой симметрии (рис.5.28). Из условий равновесия найдем В = ·Р/2, А = Р/2; тем самым найдены нормальные силы.

Для поиска угла поворота φ возвращаемся к исходной задаче (рис.5.27), снимаем нагрузку Р и прикладываем пару сил моментом 1 (рис.5.29).Чтобы воспользоваться интегралом Мора, нужно построить эпюру нормальных сил в этой вспомогательной задаче. Здесь симметрии нет ("Э" показана на рис.5.30). Нетривиальных условий равновесия - четыре, неизвестных - пять; задача статически неопределима.

Пользуясь разрешением принять во вспомогательной задаче неизвестную метода сил произвольно (что бы она собой ни представляла), примем, например, что =0. Из равновесия жесткого стержня следует, что и N₃ = 0. Равновесие левого стержня требует значения А = - 1/l и, возвращаясь к горизонтальному, найдем остальные неизвестные: = - ·l, В = 1/l. Все нормальные силы найдены (= B=1/l), из интеграла Мора находим φ:

.

Чуть менее громоздко эту задачу можно было решить, используя симметрию (косую) исходной задачи: поворот обоих стержней 1 одинаков. Найдем сумму углов поворота этих стержней, приложив, во вспомогательной задаче, соответственно, две единичные одинаково направленные пары сил (рис.5.31, 5.32). Равновесие вертикальных стержней требует A^BC = 1/l; горизонтального - C^BC = /l, B^BC = 1/l . Интеграл Мора:

,

что совпадает с предыдущим ответом.