8. Устойчивость упругих систем

8.1. Что такое критическая сила?

Рассматривая этот раздел сопротивления материалов, следует обратить внимание на следующие его особенности. Во-первых, если раньше нас интересовало лишь, при каких условиях конструкция находится в равновесии, то сейчас мы анализируем качество равновесия: оказывается, для прочности конструкции это бывает крайне важно. Если равновесие неустойчиво, то при любом малом возмущении (а избежать его практически невозможно) система переходит в другое положение, не предусмотренное условиями ее работы; при этом происходит нежелательное перераспределение усилий в ее элементах.

Во-вторых, приходится отказаться от одной из основных гипотез сопротивления материалов - гипотезы малости перемещений (называемой принципом начальных размеров), так как в рамках этой гипотезы равновесие всегда устойчиво, если устойчив материал конструкции. Таким образом, изучая по-прежнему относительно малые смещения точек тела при его нагружении, мы уже не рассматриваем их как бесконечно малые. С этим связана третья особенность: даже в пределах закона Гука задача перестает быть линейной; становится несправедливым и принцип суперпозиции.

Типы равновесия проще всего увидеть на примере весомого шарика, лежащего на поверхности, рельеф которой показан на рис.8.1. Здесь П - высота рельефа как функция координаты х; одновременно, это. потенциальная энергия шарика, деленная на постоянную величину - вес шарика.

Нетрудно видеть, что равновесие наблюдается лишь в четырех положениях из показанных пяти.

Положение 3 наиболее типично для механических систем (простейшую из которых мы рассматриваем): это устойчивое равновесие. Малые возмущения, смещающие шарик влево или вправо, выводят его из начального положения равновесия и переводят в смежное положение - бесконечно близкое к исходному, но после их снятия шарик возвращается в исходное положение.

Положение 4 в этом отношении наиболее неприятно: любое малое возмущение выводит шарик из положения равновесия, и он скатывается до нахождения другого. Такое состояние системы называется неустойчивым равновесием.

Особое место занимает состояние безразличного равновесия 5. Это - единственная ситуация, когда смена положения не нарушает равновесия. Переход конструкции из устойчивого состояния в неустойчивое (при росте нагрузки) проходит через эту фазу, называемую критической; определение соответствующего (критического) значения нагрузки и представляет обычно задачу расчетчика.

Наконец, встречается "устойчивое в малом" состояние 1; оно в механике почти не изучается. Здесь при малых возмущениях шарик устойчив, однако, если возмущения больше некоторых небольших, но конечных величин, то происходит потеря данной формы равновесия.

Нетрудно заметить, что в положении равновесия шарик обладает минимальной в данной окрестности потенциальной энергией. В безразличном состоянии потенциальная энергия не изменяется при смене положения.

Для деформируемых конструкций ситуация аналогична, если считать, что величина П состоит из потенциальной энергии положения (связанной с положением точки приложения силы) и потенциальной энергии деформации. Эту сумму называют полной потенциальной энергией системы. Все приведенные выше соображения о видах равновесия (или неравновесия) остаются в силе, но рельеф поверхности П зависит от значений действующих сил. При невысоких нагрузках конструкция обычно устойчива, но при возрастании нагрузки (или температуры, или параметра кинематического воздействия) до некоторой величины ситуация изменяется: появляется новое, близкое к начальному (смежное), состояние равновесия конструкции, причем прежнее остается равновесным (бифуркация) или оказывается неравновесным, и конструкция, меняя свою форму, переходит в новое состояние равновесия. Это значение параметра нагрузки называют критическим.

В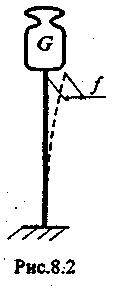 частности, при сжатии прямого вертикального стержня (задача Эйлера, рис.8.2) грузом G состояние системы «стержень - груз» характеризуется стрелой прогиба f. При невысокой нагрузке устойчивое состояние является прямолинейным (f = 0). Это можно увидеть из энергетического рельефа (рис.8.3), где П - потенциальная энергия груза в сумме с энергией сжатия стойки (практически не зависящей от f) и энергией изгиба стойки, пропорциональной квадрату f, Уменьшение высоты стойки при ее изгибе (и, соответственно, уменьшение потенциальной энергии груза) также пропорционально квадрату f, поэтому рельеф описывается квадратичной параболой. Пока груз невелик, с ростом прогиба величина П возрастает (потенциальная энергия изгиба растет быстрее, чем убывает потенциальная энергия груза, рис.8.За), но при большом весе груза ситуация обратна (рис.8.3 в). Критическому значению нагрузки G = G_* отвечает промежуточная ситуация (рис.8.3 б).