5.8. Температурные смещения

В предыдущем параграфе был рассмотрен общий случай определения смещений с помощью интеграла Мора. На практике часто приходится иметь дело с тепловыми смещениями. Ниже показаны два приема, облегчающих это дело.

Пусть внешним воздействием на статически неопределимую конструкцию является только нагрев (нет силовых воздействий), а лимитирует работоспособность не прочность, а жесткость конструкции. Температурные напряжения в этом случае можно не определять и, оказывается, статическую неопределимость в основной задаче можно не раскрывать, но следует полностью решить вспомогательную (изотермическую) статически неопределимую задачу. Покажем это.

Интеграл Мора (если опоры на месте)

(5.12)

требует, казалось бы, знания полной деформации в основной задаче:

,

где, ввиду отсутствия внешних сил, (см. выражение (5.3)). Следовательно, выражение (5.12) принимает вид

. (5.13)

Учтем, что Ф^ВС/Ж = Д^ВС (вспомогательная задача упруга) и

(5.14)

(деформации во вспомогательной задаче совместны: при ее решении мы добросовестно раскрыли статическую неопределимость, игнорируя рекомендации предыдущего параграфа). Это позволяет получить

, (5.15)

то есть для решения исходной задачи достаточно знать лишь температуры, но статическую неопределимость вспомогательной задачи следует раскрыть.

Пример 9. Пусть балка прямоугольного поперечного сечения подвергается тепловому воздействию, представ-ленному на рис. 5.33. Требуется определить угол поворота лечения А.

Решение. В исходной задаче следует определить лишь тепловые деформации осевой линии – χ^Т и . Поскольку горизонтальных связей нет, деформация не влияет ни на силы, ни на изгиб. Кривизна постоянна по длине и равна – αТ_Н/h.

Вспомогательная задача показана на рис.5.34 а. Это - статически неопределимая задача; раскрытие статической неопределимости (стандартным образом, методом сил) дает эпюру М^ВС (рис.5.34 б). Интеграл М^ВС по длине 2l равен - l/4. Соответственно, интеграл Мора определяет ответ

.

Данный прием эффективен в случаях, когда в конструкции могут варьироваться тепловые поля, а нас интересует смещение конкретной точки (например, положение рабочего органа). Тогда вспомогательная задача решается как следует, но один раз; решать температурные задачи для каждого поля температур не нужно.

Метод обобщается на произвольные тела:

или, если материал изотропен,

где σ₀ = (σ_x+σ_у+σ_z)/3 - среднее нормальное напряжение в точке конструкции х.

5.9. Метод фиктивных нагрузок

Заслуживает внимания другой нестандартный подход к решению температурных задач, предложенный в теории упругости [3]. Было показано, что задача термоупругости может быть заменена изотермической, если добавить фиктивные объемные и поверхностные нагрузки и условия равновесия записывать для фиктивных напряжений, которые связаны с деформациями (действительными, не фиктивными) обычным изотермическим законом Гука. После решения такой задачи остается лишь от найденных фиктивных напряжений перейти к действительным, а деформации и смещения корректировать не нужно.

Фиктивные объемные (отнесенные к единице объема) силы равны - тТ', где Т' - вектор-градиент температуры. Он направлен в сторону скорейшего возрастания температуры, и равен по модулю скорости роста температуры при смещении в этом направлении. Под температурой Т, как обычно, понимается нагрев (в градусах) в данной точке; m=α·E/(l - 2·μ), μ –коэффициент Пуассона.

Фиктивные поверхностные (распределенные по поверхности тела) силы направлены по нормали к поверхности и их интенсивность равна тТ. Если Т > О, эти силы направлены в сторону растяжения, при Т < 0 - в сторону сжатия. Отсюда следует, в частности, что на границе раздела двух материалов (с характеристиками m = m₁ и m = m₂) по нормали к этой поверхности должна быть приложена фиктивная распределенная по поверхности сила интенсивностью (m₁ – т₂)·Т, направленная, если эта величина положительна, в сторону второго материала.

При решении обычных задач сопротивления материалов эта несколько громоздкая схема заметно упрощается. Пусть стержень прямоугольного поперечного сечения (bxh) подвержен переменному по высоте нагреву. Рассмотрим элемент длины стержня dz (рис.5.35). Фиктивные объемные силы, действующие на элемент, сводятся к элементарной вертикальной (направленной вниз) силе

.

Таким образом, интенсивность фиктивной поперечной нагрузки dF₀/dz зависит лишь от разности температур - в верхней точке (Т_В) и в нижней точке поперечного сечения. Это справедливо лишь для данного случая: если температура изменяется и по х, или сечение не является прямоугольным, то выражение для фиктивной силы будет иным.

По четырем поверхностным граням элемента длины стержня «приложены» фиктивные поверхностные силы (интенсивность тТ) - по нормалям к поверхности. На боковых гранях они уравновешивают друг друга, их суммарная сила равна нулю. Но на верхней и нижней действуют т·Т_В (вверх) и т·Т_Н (вниз). В итоге оказывается, что сумма объемной и поверхностной силы, действующей на элемент длины, равна нулю.

Остается рассмотреть фиктивные поверхностные силы по торцам стержня (если они не защемлены): они имеют интенсивность, равную т·Т, то есть изменяются по закону изменения температуры. В итоге они сводятся к фиктивной внешней силе, действующей по нормали

(5.16)

(, S- площадь сечения, Т_ср - средняя по сечению температура), и к фиктивному внешнему моменту относительно центральной оси х

(5.17)

Здесь S_x^Т - статический момент температуры относительно оси х.

То же относится и к случаю биметаллической балки: если она нагрета равномерно по длине (и, возможно, неравномерно по высоте), то объемные и поверхностные силы по всей длине можно считать нулевыми, а на торцах каждому из металлов следует приложить фиктивные нагрузки (5.16), (5.17). Далее решение обычной изотермической задачи позволяет найти напряжения, деформации и смещения; последние - истинны, а напряжения - фиктивны, их нужно корректировать.

Фиктивные напряжения σ* отличаются от истинных σ на всестороннее равномерное растяжение величиной т·Т. Однако в задачах сопротивления материалов, объектом которых являются стержневые конструкции, нормальные напряжения в продольных площадках равны нулю, поэтому схему пересчета напряжений можно упростить.

Рассмотрим стержень произвольного сечения (вариант сечения показан на рис. 5.36), защемленный по концам и равномерно нагретый. Фиктивные объемные силы отсутствуют, фиктивные поверхностные - постоянные по длине стержня и по боковой поверхности (рис.5.36), равны т·Т. Они создают в плоскости поперечного сечения фиктивные напряжения - равномерное растяжение . Фиктивные продольные напряжения и истинные поперечные деформации ε^' находим из закона Гука, зная, что продольные деформации ε_z равны нулю по условиям закрепления:

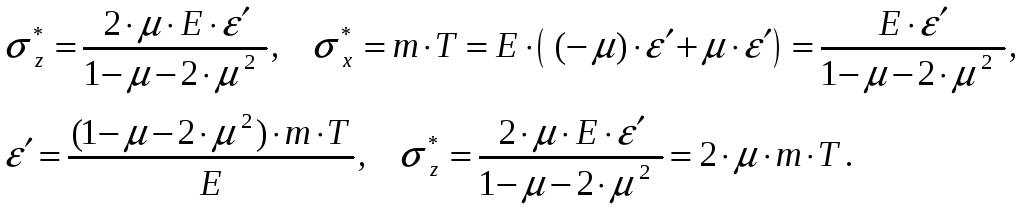
Действительные напряжения в продольных сечениях: , в поперечных - .

Итак, при решении подобных задач фиктивные объемные силы следует считать нулевыми; фиктивные поверхностные силы прикладывать только на торцах стержня (если они свободны) и считать их равными Е·α·Т. Фиктивные напряжения в поперечных сечениях связанны с истинными продольными деформациями по формуле σ* = Е·ε; после их определения находим истинные напряжения:

σ* = σ* - Е·α·Т. (5.18)

Пример 10. В равномерно нагретом биметаллическом стержне (рис.5,37 а), имеющем одинаковые размеры поперечных сечений (прямоугольник bxh), но различные значения коэффициентов теплового расширения, определить вертикальное перемещение точки А.

Решение. Модули упругости металлов одинаковы, поэтому наиболее удобен для решения задачи метод фиктивных нагрузок: в изотермической задаче фигурирует один стержень (а не два) сечением bх2h. Правый конец свободен, поэтому в фиктивной задаче к нему должна быть приложена фиктивная нагрузка интенсивностью Е·α·Т. Она дает две равнодействующие Е·α₁·Т·S₁ и Е·α₂·Т·S₂ (рис.5.37 б), где S₁ = S₂ = S = b·h. Методом сечений найдем внутренние силовые факторы, постоянные по длине (рис.5.37 в):

.

Нормальная сила не влияет на вертикальные перемещения; изгибающий (фиктивный) момент определяет обычным образом кривизну χ = M/(E·J) (J=b·(2·h)³/12), кривизна в этом выражении является действительной.

Соответствующая поставленному вопросу вспомогательная эпюра показана на рис.5.37 г. В соответствии с интегралом Мора

.

Найденное перемещение является истинным (не фиктивным). В случае, когда E₁ ≠ E₂, S₁ ≠ S₂ и T ≠ const задача несколько более громоздка, но это почти стандартная задача сопротивления материалов. Пример решения такой задачи приведен в разделе 3 (задача 9).

Пример 11. Пусть требуется определить угол поворота сечения А в задаче из примера 9 (рис.5.33).

Решение. К торцам балки прикладываем фиктивную распределенную нагрузку интенсивности q*=α·T·E (рис.5.38а). Она может быть заменена силами N^* = 3·q^*·S/2 и моментами M^* = q^*·b h²/12 (рис.5.38 б). Раскрываем статическую неопределимость, находим эпюру фиктивных изгибающих моментов (рис.5.38 в). Для определения перемещений строим эпюру M^BC (рис.5.38 г) во вспомогательной задаче, приложив единичный момент в сечении А и приняв, для простоты, что правая опорная реакция равна нулю (поскольку основная задача решена полностью, то во вспомогательной значение произвольно). Ответ, естественно, получаем тот же, что и в примере 9.

Решите самостоятельно

Для систем, изображенных на рис.5.39 и 5.40, постройте эпюры Ф (задачи, с учетом симметрии, статически определимы). Чему равен относительный угол поворота сечений A и B, A и С?