2.3. Задача распределения температуры в тонком стержне

Рассмотрим прикладную задачу из области математического моделирования – задачу о распределении температуры в тонком стержне [3].

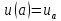Имеется тонкий стержень длины l. Его левый конец закреплен в точке a = 0, а правый, соответственно, в точке b = l. На левом конце стержня поддерживается температура , а на правом – температура 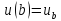. Известны следующие физические характеристики стержня:

k(x) – коэффициент теплопроводности материала, из которого состоит стержень;

q(x) – коэффициент теплоотдачи материала;

f(x) – плотность внутренних источников тепла (стоков тепла, если f(x) < 0).

Требуется определить температуру u(x) в каждой точке стержня после установления равновесия.

Решение поставленной задачи сводится к решению первой краевой задачи для одномерного стационарного уравнения теплопроводности:

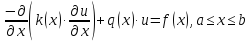, (2.5)

. (2.6)

В качестве физических характеристик возьмем конкретные значения, при этом уравнение (2.5) примет следующий вид:

,

.

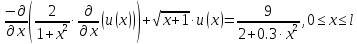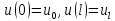Для численного решения первой краевой задачи теплопроводности может быть применена схема конечных разностей. Для этого область непрерывного изменения аргумента заменяют дискретным множеством точек, называемых сеткой. Введение равномерной сетки для рассматриваемой задачи показано на рис. 2.4.

Рис. 2.4. Разбиение стержня на n равных участков

Вместо функций непрерывного аргумента рассматривают функции, определенные только в узлах сетки, – сеточные функции. Производные, которые входят в дифференциальное уравнение (2.5), заменяют их разностными аналогами – линейными комбинациями значений сеточных функций в некоторых узлах сетки. В результате краевую задачу заменяют дискретной краевой задачей (разностной схемой), представляющей собой систему конечного числа линейных алгебраических уравнений. Решение разностной схемы принимают за приближенное решение краевой задачи (2.5)-(2.6) [3].

В зависимости от требуемого порядка точности, дискретные соотношения для производных могут быть разными. В частности, второй порядок точности имеет вид:

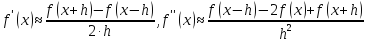. (2.7)

В этом случае приходим к СЛАУ вида:

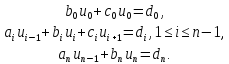(2.8)

Заметим, что СЛАУ вида (2.8) обладают свойством диагонального преобладания в силу специфики вычисления коэффициентов, это значит, что для их решения можно использовать предложенную модификацию метода Якоби.

2.4. Вычислительный эксперимент

Для поставленной задачи была проведена серия вычислительных экспериментов на кластере МЭИ (схема его архитектуры представлена на рис. 1.3). При всех запусках выбиралась точность вычислений 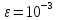, а количество узлов сетки назначалось от 500 до 5000 (каждый узел сетки соответствует одному уравнению в системе 2.8). Эксперименты проводились в двух режимах: без проверки блоков, состоящих из нулей и с проверкой. В первом случае ускорение достигалось только за счет параллелизма, а во втором – за счет параллелизма и экономии на «лишних» умножениях матрицы на вектор. Временные характеристики решений задач представлены в таблице 2.2.

Таблица 2.2. Результаты вычислительного эксперимента решения СЛАУ разреженного типа

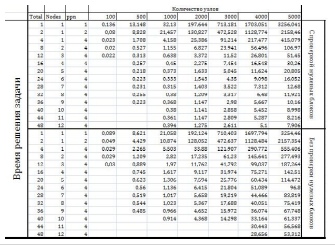
Для наглядного представления временных характеристик на основе значений из таблицы 2.2 приведем на рис. 2.5 график ускорений параллельного решения СЛАУ.

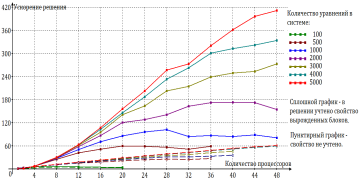
Рис. 2.5. Зависимость ускорения параллельного решения СЛАУ от ресурсов

Ускорение параллельного решения с учетом разреженности матрицы коэффициентов СЛАУ существенно превосходит ускорение, полученное без учета специфики разреженности системы. На графиках ускорений параллельных решений с учетом «нулевых» блоков для 500, 1000 и 2000 уравнений наблюдаются пики, смещающиеся вправо с ростом размерности системы. Наличие пиков – закономерное явление, объясняемое тем, что при росте числа процессоров увеличивается не только вычислительная мощность системы, но и задержки на обменные взаимодействия между ее узлами. Отсюда вывод: для решения предложенной системы, например, из 2000 уравнений целесообразно использовать от 32 до 36 процессоров. Дальнейшее увеличение вычислительных ресурсов не только не увеличит ускорение, а уменьшит его. Чем выше размерность системы, тем большее число процессоров можно порекомендовать использовать для ее решения.