2.2. Особенности разработки последовательно-параллельной модификации метода якоби
Основная
цель разработки модификации метода
Якоби – уменьшить время решения класса
СЛАУ, для которых применим классический
метод Якоби, а именно для разреженных
систем, обладающих свойством диагонального
преобладания. Моделью параллельных
вычислений выбрана модель передачи
сообщений между главным и подчиненными
процессами. Процесс выполняет свою
часть задачи. Среди всех выделен главный,
который помимо своей части вычислений
отвечает за рассылку исходных данных
всем исполнителям и прием их результатов.
Данные в программе хранятся в матричном
виде, использовано их блочное разбиение.
Количество уравнений, отправляемых на
каждый процесс, равно отношению числа
всех уравнений к количеству процессов,
округленному вверх, например:
.
На рис. 2.1 показано, как матрица в общем
виде распределяется по трем процессорам.
Рис. 2.1. Пример распределения системы по трем процессам.
Фрагменты матриц коэффициентов, попавшие на процесс, представляют собой прямоугольные матрицы. Эти матрицы разбиваются на набор квадратных матриц (блоков). Если число переменных или уравнений не кратно размерности блока, блок дополняется нулевыми элементами. Как показано на рис. 2.2, в результате разбиения получаются квадратные блоки.
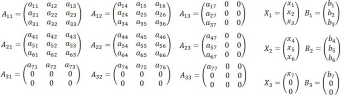
Рис. 2.2. Пример разбиения системы на блоки
Вектора решения и правой части разбиваются на фрагменты векторов столбцов по такому же принципу (рис. 2.2). Разбиение СЛАУ на блоки позволяет использовать при решении блочную схему метода Якоби:
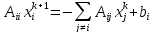. (2.3)
Заметим, что для выполнения следующего уточнения вектора решения необходим вектор, полученный на предыдущей итерации. Поэтому, при завершении итерации, фрагменты решения, полученные на отдельных исполнителях, собираются на главном, а затем в начале следующей итерации распространяются по всем процессам. Итерационный процесс продолжается до тех пор, пока не выполнено условие (2.4).
, (2.4)
где B – матрица коэффициентов, приведенная к виду, удобному для итераций [3].
Графически изложенный алгоритм изображен на следующем рис. 2.3.
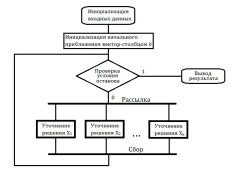
Рис. 2.3. Последовательно-параллельная модификация блочного метода Якоби.
Обратим
теперь внимание на вычислительный
процесс, проходящий в блоках «Уточнение
решения». В каждом блоке проводятся
вычисления, описанные формулой (2.3), в
которой присутствует относительно
затратная с вычислительной точки зрения
операция умножения матрицы на вектор.
Учитывая то, что рассматриваемая
модификация ориентирована на решение
разреженных систем, весьма высока
вероятность того, что матрица
из формулы (2.3) может состоять только из
нулевых элементов и соответствующее
ей слагаемое никак не повлияет на сумму.
Представляется целесообразным перед
перемножением матрицы на вектор
предварительно проверять, не является
ли она нулевой. Отметим также, что при
использовании такого подхода применительно
к плотно заполненным матрицам, получаем
результат за немного большее время в
силу того, что тратится время на проверку,
а перемножение все равно осуществляется.
Однако проверка себя оправдывает, так
как в результате экспериментов
установлено, что величина задержки не
превосходит 5-7% от общего времени решения
систем с плотно заполненными матрицами
коэффициентов. Для разреженных систем
выигрыш во времени решения весьма
ощутим.