2.1. Сравнение класических методов решения слау

При решении СЛАУ на ЭВМ ставят целью нахождение некоторого приближенного решения 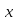(с заданной точностью) системы уравнений:

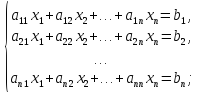
или в матричной форме

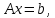
где 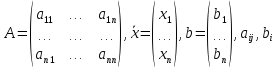- постоянные вещественные коэффициенты,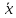– точное решение системы,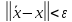[3].

Среди всех способов нахождения решения СЛАУ традиционно выделяют два типа методов: прямые и итерационные методы. Прямые методы направлены на получение точного решения систем и являются, как правило, более трудоемкими. Цель итерационных методов – нахождение некоторого приближения к точному решению.

Рассмотрим наиболее известные классические прямые методы решения СЛАУ.

Метод Гаусса – пожалуй, самый известный прямой метод решения систем. Он заключается в последовательном исключении переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которого последовательно, начиная с последних по номеру переменных, находятся все остальные. Преимущества этого метода – доступность алгоритма и наличие большого количества модификаций. Однако метод имеет весьма серьезный недостаток, не позволяющий широко использовать его в расчетах, – высокая трудоемкость метода [3]. Количество арифметических операций связано с размерностью 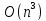, поэтому для больших систем метод Гаусса практически не применим.

Метод на основе LU-разложения [3] – известный прямой метод, являющийся одной из модификаций метода Гаусса. Его суть в получении из исходной матрицы коэффициентов двух матриц: L – нижней треугольной матрицы и U – верхней треугольной матрицы. Основная сложность алгоритма в их получении. Решение находится на фазе обратного хода. Преимущество этого метода в том, что при решении более одной системы с одинаковыми матрицами коэффициентов, но разными правыми частями, полученные при решении матрицы L и U будут такими же для всех последующих систем. Основной недостаток метода LU-разложения все в той же высокой трудоемкости.

Еще одна разновидность разложения исходной матрицы коэффициентов в произведение двух других представлена в методе Холецкого [3]. С помощью этого метода на решение систем с симметричной матрицей коэффициентов достаточно затратить в два раза меньше арифметических операций, чем потребуется при решении методом Гаусса. Однако применимость этого метода ограничивается симметричными системами.

Если необходимо решить разреженную ленточную СЛАУ, часто применяют метод прогонки [3]. Суть метода в выводе специальных соотношений (прогоночных коэффициентов). Основное преимущество этого метода в его экономичности: зависимость числа арифметических операций от размерности линейная. Однако метод имеет ряд недостатков. Главный из них – метод прогонки не универсален. Составленные прогоночные коэффициенты для системы с одним портретом матрицы коэффициентов отличаются от коэффициентов для системы с другим портретом. Иными словами, для каждого нового портрета матрицы коэффициентов необходимо заново выводить прогоночные коэффициенты.

Обратимся к рассмотрению итерационных методов решения СЛАУ. Большинство из них сводится к проведению своего итерационного процесса над некоторым приближением к решению. С каждой новой итерацией получаемое решение ближе к точному, если метод является сходящимся для взятых системы и начального приближения. Итерационный процесс проводится до тех пор, пока решение, полученное на очередной итерации не будет удовлетворять некоторому критерию точности. Общий недостаток итерационных методов – зависимость от начального приближения. Из-за этой зависимости, вообще говоря, нет гарантии, что метод сойдется (достигнет достаточно близкого к точному решение) за конечное число шагов. Однако для многих итерационных методов доказано, что они сходятся при любом начальном приближении к точному решению при выполнении определенных условий.

Метод Якоби [3] сводится к проведению следующего итерационного процесса:

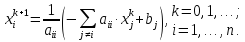(2.1)

Достаточное условие сходимости: 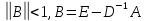,E – единичная матрица, D – диагональная. При выполнении более жесткого условия – диагонального преобладания матрицы коэффициентов – метод также сходится при любом начальном приближении.

Метод Гаусса-Зейделя является своего рода улучшением метода Якоби. Усовершенствование состоит в немедленном использовании полученных значений:

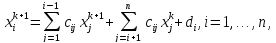(2.2)

где матрица C и столбец d получаются преобразованиями исходной матрицы коэффициентов и вектор-столбца правых частей [3].

Преимущества этого метода: он сходится даже быстрее, чем метод Якоби. К недостаткам его относят все недостатки метода Якоби. Помимо них, для вычисления очередной компоненты вектора приближенного решения необходимо сначала получить предыдущую. Это обстоятельство не позволяет применять аппарат параллельных вычислений к методу Гаусса-Зейделя.

Основные преимущества и недостатки обоих типов методов сведены в таблице 2.1.

Таблица 2.1. Преимущества и недостатки прямых и итерационных методов

	Прямые методы	Итерационные методы
преимущества	позволяют получить решение за конечное число операций; не зависят от выбора начального приближения; погрешность решения определяется машинным .	позволяют найти решение с заданной степенью точности; сохраняют свойство разреженности матрицы коэффициентов; число операций порядка ; эффективно используют оперативную память.
недостатки	число операций порядка ; приводят к потере свойства разреженности матрицы коэффициентов.	нет гарантии сходимости в общем случае; область применения конкретного метода зависит от свойства сходимости.

Приходим к следующему выводу: прямые методы не целесообразно применять при решении СЛАУ высокой размерности: во-первых, для хранения требуется большой объем оперативной памяти; во-вторых, велико количество арифметических операци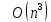й ; в-третьих, в процессе решения свойство разреженности матрицы коэффициентов может быть утеряно; в-четвертых, точного решения при выполнении на вычислительной машине, вероятнее всего, получить не удастся из-за наличия погрешности, неизбежно возникающей в результате выполнения операции деления [3]. Итерационные методы обладают рядом преимуществ для систем большой размерности: требуют меньше оперативной памяти и выполнения арифметических операций, сохраняют свойство разреженности систем и позволяют регулировать величину погрешности.

В силу того, что в настоящей работе рассматриваются разреженные системы большой размерности, возьмем за основу для составления последовательно-параллельной модификации итерационный метод Якоби.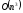