9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.

*общее предисловие к вопросам 8 и 9 В задаче линейного программирования (ЛП) кроме уравнений-ограничений существует ещё и линейная функция L  c0  c1x1  ... cjxj  ... cnxn, => нужно минимизировать. После замены xj  yi её нужно выразить через новые свободные переменные x1, x2,..., xj1, yi , xj1,..., xn. Для этого можно использовать тот же алгоритм, что и для преобразования любой строки таблицы. Действительно, т.к. L  c0  (1x1 ... jxj ... nxn ) , где 1  c1; 2  c2; ... n cn, мы получим её одну строку (добавочную) стандартной таблицы, в которой никогда не выбирается разрешающий элемент. С помощью табличного алгоритма обмена переменных в уравнениях основной задачи ЛП (ОЗЛП) можно решить любую задачу ЛП. Нахождение решения распадается на 2 этапа=> т.е. на 8 и 9 вопрос (отыскание опорного решения и отыскание оптимального решения).

Отыскание оптимального решения, минимизирующего линейную функцию L – т.е. попутно выясняется, ограничена ли снизу минимизируемая функция L.

Надо найти такое опорное решение, которое обращает в минимум линейную функцию

L  c₀  (₁x₁ ... _jx_j ... _nx_n ).

Принципиальную сторону вопроса мы уже рассматривали (как я поняла это то, что в табличке выше, но это не точно, мб сюда что-то из 2 вопроса). Здесь мы на примере покажем, как эта оптимизация м. б. проведена с помощью табличного алгоритма замены x_j  y_i .

Сформулируем правила нахождения оптимального решения симплекс-методом.

1) Если все свободные члены (не считая строки L) в симплекс таблице неотрицательны, а в строке L (не считая свободного члена) нет ни одного

положительного элемента, то оптимальное решение достигнуто.

2) Если в строке L есть положительный элемент, а в столбце, соответствующем ему,

нет ни одного положительного элемента, то линейная функция L не ограничена

снизу и оптимального решения не существует.

3) Если в этом столбце есть положительные элементы, то следует произвести замену одной из свободных переменных на одну из базисных, причём в качестве разрешающего надо взять тот элемент этого столбца, для которого отношение к

нему соответствующего свободного члена минимально.

Пример

Найти решение задачи ЛП с уравнениями

y1  2  (x1  x2  2x3);

y2 1 (x1  x2  x3);

y3  5 (x2  x3);

y4  2  (2x1  x2);

обращающее в минимум линейную функцию L  0 (x1  2x2  x3).

Решение

Т.к. все свободные члены неотрицательны, то опорное решение налицо:

x₁  x₂  x₃  0; y₁  y₄  2; y₂ 1; y₃  5; L  0

Это решение не оптимально, т.к. коэффициент при x₂ и x₃ положительны (у линейной функции). Выберем x₃, его надо поменять.

	Св. член	x1	x2	x3, x3  y2
L	0 -1	-1 -1	2 1	1 -1
y1	2 2	1 2	1 -2	-2 2
y2 , y2  x3	1 1	1 1	-1 -1	1 λ=1
Y3	5 -1	0 -1	1 1	1 -1
y4	2 0	2 0	-1 0	0 0

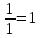; - это для строки y_2.

; - это для строки y_3.

По min выбираем y_2.

	Св. член	x1	x2, x2  y3	y2
L	-1 -6	-2 3/2	3 -3/2	-1 3/2
y1	4 2	3 -1/2	-1 1/2	2 -1/2
x3	1 2	1 -1/2	-1 1/2	1 -1/2
y3, y3  x2	4 2	-1 -1/2	2 λ=1/2	-1 -1/2
y4	2 2	2 -1/2	-1 1/2	0 -1/2

	Св. член	x1	y3	y2, y2  y1
L	-7 -2	-1/2 -5/6	-3/2 -1/6	1/2 -1/3
y1 , y1  y2	6 4	5/2 5/3	1/2 1/3	3/2 λ=2/3
x3	3 -2	1/2 -5/6	1/2 -1/6	1/2 -1/3
x2	2 2	-1/2 5/6	1/2 1/6	-1/2 1/3
y4	4 2	3/2 5/6	1/2 1/6	-1/2 1/3

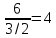; - это для строки y_1.

; - это для строки x_3.

По min выбираем y_1.

	Св. член	x1	y3	y1
L	-9	-8/6=-4/3	-10/6=-5/3	-1/3
y2	4	5/3	1/3	2/3
x3	1	-2/6=-1/3	2/6=1/3	-1/3
x2	4	1/3	4/6=2/3	1/3
y4	6	14/6=7/3	2/3	1/3

Т.к. в строке L нет ни одного положительного элемента, то оптимальное решение достигнуто.

x₁  y₃  y₁  0; y₂  x₂  4; x₃ 1; y₄  6; L  9.