Некоторые выводы

1) Решение основной задачи ЛП не может лежать внутри ОДР, а может лежать только на границе, т.к. находим экстремально удаленную точку.

2) Решение общей задачи может быть не единственным, когда оптимум достигается на всей стороне многоугольника (когда решений бесконечное множество).

3) Основная задача может не иметь решения, даже если существует ОДР. Когда ОДР не ограничена сверху (открытая область), в таком случае решения не существует.

4) Оптимальное решение всегда достигается в одной из вершин многоугольника ОДР. Решение, лежащее в одной из вершин – опорное решение, а сама вершина – опорная точка.

5) Для того, чтобы найти оптимальное решение достаточно перебрать все вершины (все опорные точки) и выбрать из них ту, в которой L минимальна.

6) Если число свободных переменных = 2, а число базисных m и решение основной задачи существует, то оно всегда достигается в одной из точек, где по крайней мере 2 из переменных обращаются в ноль.

7) Если (m<n) на 3, т.е. n-m=3, то мы приходим к случаю геометрической интерпретации в трехмерном пространстве.

Изменится: - каждое условие-ограничение не прямая, а плоскость

- ОДР если существует – выпуклый многогранник, ограничивающий часть пространства, для которой х₁ ≥ 0, х₂ ≥ 0, …, х_n ≥ 0.

- Вместо основной прямой L’=0 имеем основную плоскость, которую также мысленно будем перемещать относительно самой себя.

Опорные точки заменяются на опорные вершины.

Такую же интерпретацию можем распространить и на n-мерное пространство.

5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.

Пусть имеется задача ЛП с n переменными х₁, х₂, …, х_n.

Ограничения имеют вид неравенств (≥0, ≤0).

Методом перестановки приводим к тому, чтобы у всех неравенств стоял знак ≥0. Тогда ограничения могут принять вид:

(*)

Требуется найти такие неотрицательные х₁, х₂, …, х_n, которые удовлетворяют (*) и обращают L в минимум

[ L = C₁*x₁ + C₂*x₂ + … + C_n*x_n ]

Алгоритм решения подобных задач:

1) Вводят новые переменные:

(**)

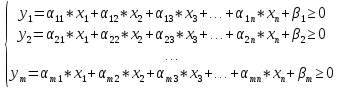y₁, y₂, …, y_m – добавочные переменные (также )

Тогда возникает новая задача ЛП – найти такие неотрицательные значения (n+m) переменных (х₁, х₂, …, х_n) и (y₁, y₂, …, y_m), чтобы они удовлетворяли системе (**) и обращали L в минимум.

2) Переход к классической постановке задачи.

В такой постановке (х₁, х₂, …, х_n) рассматриваются как свободные переменные, а (y₁, y₂, …, y_m) – базисные.

Отличия: функция L сразу выражена через свободные переменные. Если свободных переменных только 2, то используем геометрический метод, а если их больше, то используем вычислительные методы.

Пример (прикрепляю фото из лекции за 03.03)

6) Симплекс-метод решения задачи лп.

Для нахождения решения задачи ЛП в общем случае при произвольном числе свободных переменных, используются не геометрические, а вычислительные методы. Из них наиболее универсальный – Симплекс-метод.

Пусть задача ЛП имеет n переменных и m уравнений-ограничений. Будем считать все уравнения независимыми. Мы знаем, что оптимальное решение достигается в одной из опорных точек ОДР, где по крайней мере k переменных (k=n-m) обращается в ноль.

Алгоритм решения:

1) Выберем k свободных переменных х₁, х₂, …, х_k

2) Оставшиеся (базисные) выразим через эти свободные, тогда получим m уравнений следующего вида:

m штук уравнений

3) Мы знаем, что опорное решение точно достигается в точке, в которой свободные переменные равны 0, т.е. х₁ = х₂ = … = х_k = 0, тогда базисные переменные будут равные свободным членам , такое опорное решение допустимо если все β_i , i = будут .

Если какое-то β_i < 0, то такое решение – недопустимо и нужно искать не оптимальное, а опорное решение.

Допустим, что все β_i, тогда мы нашли опорную точку.

4) Для того, чтобы определить оптимальное решение мы должны через свободные переменные выразить L. Тогда L = γ₀ + γ₁*x₁ + γ₂*x₂ + … + γ_n*x_n

Если все коэффициенты при х₁, х₂, …, х_k 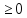, то оптимум достигнут. При этом это оптимальное решение L_min = γ₀.

Но если любой коэффициент имеет отрицательное значение, то имеет смысл соответствующую переменную сделать положительной, что позволит уменьшить значение L. Но так как опорное решение находится в точке, в которой k переменных должны быть равны 0, необходимо некоторую другую (из числа базисных) прировнять к 0.

Иными совами, нужно обменять 2 переменных: свободную и базисную.

Допустим, что γ₁ < 0. Переменную x₁ делаем положительной и меняем на базисную. Но из базисных переменных на обмен нужно выбрать ту, к которой:

1. Коэффициент при x₁ также имеет отрицательное значение.

2. Которая быстрее всего обращается в 0 при увеличении x₁.

Допустим это строка x_l = .

В опорном решении х₂ = … = х_k = 0.

Тогда, решение в опорной точке: x_l = , нам нужно, чтобы x_l быстрее стремилось к 0, при возрастании x₁.

Тогда, придадим x_l = 0: x₁ = – (Это отношение свободного члена к абсолютному коэффициенту должно быть минимальным из всех строк) (должно быть меньше всего для поиска нужной строки).

Искать оптимальное решение можно только если мы находимся в опорной точке.

5) Переразрешим систему уравнений-ограничений, относительно новых свободных переменных. Вместо x₁ используем x_l.

6) Переходим в новому опорному решению, в котором все переменные равны 0. x_l становится базисной.

7) Выразим функцию L через эти новые свободные переменные:

L = γ₀⁽¹⁾ + γ₂⁽¹⁾*x₂ + … + γ_k⁽¹⁾*x_k + γ_l*x_l .

Пример (прикрепляю фото из лекции за 03.03)