2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.

Начало из вопроса 1 (от начала до основные математические модели.

3) Оценка операции по нескольким показателям.

Пусть у нас имеется несколько показателей эффективности (группа целевых функций): w₁, w₂, …, w_k. Одни из них нужно максимизировать, а другие минимизировать.

Достижение МАКСИМАЛЬНОГО ЭФФЕКТА при МИНИМАЛЬНЫХ ЗАТРАТАХ – некорректная формулировка задачи, так как практически невозможна.

Поэтому, мы достигаем МАКСИМАЛЬНОГО ЭФФЕКТА при ЗАДАННЫХ ЗАТРАТАХ (т.е. мы фиксируем затраты)

или

достигаем ЗАДАННОГО ЭФФЕКТА при МИНИМАЛЬНЫХ ЗАТРАТАХ (т.е. параметры ограничиваются).

Пути решения:

а) Отбрасывание заведомо плохих вариантов.

Пусть дано 2 показателя: s – стоимость лекарств, w – вероятность раннего выздоровления.

Нам нужно МИНИМИЗИРОВАТЬ s и МАКСИМИЗИРОВАТЬ w.

Логично рассматривать элементы обведенные зеленым кружком. Следовательно, остальные можно отбросить.

б) Использование составных критериев.

, но это не очень хороший показатель, т.к. если знаменатель устремить к 0, то числитель роли играть не будет.

Тогда, для компенсации недостатка одного другим используют составные критерии в виде взвешенной суммы.

в) Использование составных критериев в виде взвешенной суммы.

u = a₁*w₁ + a₂*w₂ + … + a_k*w_k, где a_i – коэффициенты, которые связаны со степенью важности.

При этом естественно задать коэффициенты следующим образом:

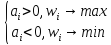
г) Сведение к одному показателю с некоторыми ограничениями.

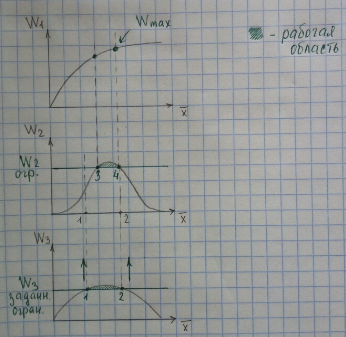
Многоэтапная процедура. Показатели эффективности (ПЭф) ранжируются по весу.

Задача: нахождение max первого показателя при ограничении оставшихся.

Мои корявые объяснения: Идем снизу вверх. Каждый показатель имеет свое ограничение. Все эти ограничения накладываются друг на друга, оставляя все меньшую рабочую область. В итоге на самом верху, остается маленький кусочек на котором определяем min и max, в зависимости от того, что нам надо.

3) Основная задача линейного программирования (озлп). Допустимые решения и оптимальное решение задачи лп.

ВСТУПЛЕНИЕ (вдруг нужно будет для полноты ответа)

Во многих практических приложениях возникают своеобразные задачи оптимизации решений, для которых характерны следующие черты:

1. Показатель эффективности (w) – представляет собой линейную функцию от элементов решения (x_i).

2. Ограничительные условия (элементы α) имеют вид линейных равенств или линейных неравенств.

Такие задачи оптимизации – задачи линейного программирования.

Рассмотрим задачу, где ограничительные условия (элементы α) имеют вид линейных равенств – ОСНОВНУЮ ЗАДАЧУ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ОЗЛП).

Формулировка основной задачи линейного программирования.

Имеется ряд переменных х₁, х₂, …, х_n. Требуется найти такие неотрицательные (≥0) значения этих переменных, которые бы удовлетворяли системе линейных уравнений (СЛУ) следующего вида:

С лекции: (*) i = , j = aij – заданные постоянные коэффициенты

И, кроме того, обращали бы линейную функцию в минимум

С лекции: L = (**)

xj – элементы решения cj – заданные постоянные коэффициенты

В некоторых задачах функция L может максимизироваться. Ее также можно привести к стандартному виду, поменяв знак.

Допустимое решение основной задачи (ДРОЗ) – любая совокупность решений х_j ≥ 0, j = . Которая удовлетворяет (*).

Оптимальное решение – то из допустимых решений, которое удовлетворяет (**), т.е. обращают L в минимум.

Основная задача ЛП необязательно должна иметь решение.

СЛУ (*) может как иметь так и не иметь решений.

Может оказаться так, что допустимые решения основной задачи (ДР ОЗ) существуют, но среди них нет оптимального: функция L в области допустимых решений не ограничена сверху.

Рассмотрим вопрос о существовании оптимальных решений.

Рассмотрим вопрос о существовании допустимых решений.

При рассмотрении данного вопроса можно не рассматривать линейную функцию L.

В линейной алгебре доказывается, что для совместимости системы линейных уравнений (СЛУ) необходимо и достаточно, чтобы ранг матрицы системы (r_c) был равен рангу расширенной матрицы (r_р).

СЛУ имеет решение при r_c = r_p.

Очевидно, что r ≤ m (число уравнений) и r ≤ n (число неизвестных).

Мы это писали на паре (скорее всего, пригодится).

Матрица СЛУ – таблица, составленная из коэффициентов при неизвестных х₁, х₂, …, х_n.

[aij], i = , j =

Расширенная матрица – матрица системы, дополненная столбцом свободных членов.

Ранг – наибольший порядок отличного от нуля определителя, который можно получить, исключая, строки и столбцы, чтобы перейти к квадратной матрице.

Пример: определить является ли совместной система СЛУ:

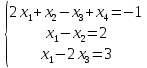
Матрица системы: 2 1 -1 1 1 -1 0 0 1 0 -2 0

Расширенная матрица системы: 2 1 -1 1 -1 1 -1 0 0 2 1 0 -2 0 3

Выделим матрицу 3х3 и найдем определитель

2	1	-1
1	-1	0
1	0	-2

Определитель Δ = 5 (перебираем все определители матрицы системы и расширенной матрицы) они все между собой будут равны, следовательно, система совместна, т.к. r_c = r_p.

На самом деле r показывает число независимых линейных уравнений.

Рассмотрим следующие случаи:

1) r = n (ранг равен числу неизвестных) Система имеет единственно решение: x_j = Δ_j / Δ

(определитель матрицы, где j-тый столбец заменили на свободные члены / обычный определитель)

Если все x_j положительные, то найденное решение является допустимым и оно же является оптимальным.

Если хоть какой-то x отрицательный, то система решений не имеет.

2) r = m (ранг равен числу уравнений)

Система имеет бесконечное множество решений, т.е. совокупность значений x₁, x₂, …, x_n, удовлетворяющий уравнениям – ограничениям.

Если среди этих решений нет ни одного, для которого все x₁, x₂, …, x_n неотрицательны, это значит, что основная задача не имеет допустимого решения.

Если же есть какие-то решения системы, для которых все x₁, x₂, …, x_n неотрицательны, то каждое из них допустимо.

Возникает вопрос – какое из допустимых решений будет оптимальным. Решение производится в зависимости от соотношения n и m.

n – m = 2	n – m > 2
Геометрический способ решения	Вычислительные способы решения

Используется прием:

1) (n-m) – количество свободных переменных, остальные переменные – базисные.

2) В области этих свободных переменных ищем ОДР.