19. Решение игр mх2.

Все тоже самое пишем, как для 2xn. Но заменяем следующее

Решение игры mx2 осуществляется аналогично. Но в этом случае строится графическое изображение игры для игрока В и выделяется не нижняя, а верхняя граница выигрыша, и на ней находится точка оптимума с наименьшей ординатой (минимакс).

ОЧЕНЬ ПРИКОЛЬНАЯ ФИГНЯ МОЖНО ЗАФИГАЧИТЬ В КОНЕЦ КАК ИТОГ

ДЛЯ NX2

1. строится графическое изображение игры;

2. выделяется нижняя граница выигрыша и находится наибольшая ордината нижней границы, которая равна цене игры γ;

3. определяется пара стратегий, пересекающихся в точке оптимума M. Эти стратегии являются активными стратегиями игрока B. Если в точке оптимума пересекаются более двух стратегий, то в качестве активных стратегий может быть выбрана любая пара из них;

4. решается полученная игра 2x2.

Решение игры mx2 осуществляется аналогично. Вместо пункта 2 применяется:

2. Выделяется верхняя граница выигрыша, и на ней находится точка оптимума с наименьшей ординатой.

КАК У НЕЕ В МЕТОДЕ, НО ДЛЯ НАШЕГО СЛУЧАЯ

Игры mx2 можно легко решить с помощью геометрического способа. Они задаются матрицей игры (табл.1), а на рис.1 показана геометрическая интерпретация этой игры для случая m=4.

Таблица 1

Ai	Bj
	B1	B2
A1	a11	a12
A2	a21	a22
………
Am	am1	am2

Рисунок 1

Геометрическое построение осуществляется так же, как и для игры 2х2, только число наклонных линий получается равным m, по числу стратегий для игрока A. Нижняя граница игры может быть сложной ломанной линией, максимум которой определяет решение игры.

Из рис.1 нижняя граница выигрыша А₂NMА₁, ее минимум достигается в точке N, которая определяет оптимальную стратегию . Стратегия A₃ вообще может не рассматриваться как заведомая невыгодная игроку A, а значения q₁ и q₂ можно найти по формулам игры 2х2, учитывая, что в точке N активных стратегий игрока А только две, А₂ и А₄.

20. Решение игр mxn.

Нельзя применять геометрическую интерпретацию.

Применяются чисто расчетные методы.

Решение любой игры mxn может быть сведено к задаче линейного программирования.

Допустим у игрока А имеется m стратегий (A₁, A₂, …, A_m), у игрока B есть n стратегий: B₁, B₂, B₃. Игра задается матрицей mxn . Мы ищем две оптимальные смешанные стратегии и , где p₁, p₂, …, p_m и q₁, q₂, …, q_n – вероятности применения соответствующих стратегий A₁, A₂, …, A_m и B₁, B₂, …, B_n и .

Для нахождения полагаем, что цена игры 𝛄 положительна (𝛄 ≥ 0). Если есть отрицательные члены, то мы добавляем к ним достаточно большое положительное число М (также можно умножить). На решение игры это не влияет, но в конце важно не забыть провести обратные действия с ценой игры (если прибавили вычесть, если умножили разделить) – нее написано прибавить, но потом в примере (который на стр.87) вычитают, так что делаем выводы. а вообще можно написать так: Тогда цена игры увеличится на М, а вероятности останутся теми же.

Когда мы применяем , а противник – чистую стратегию Bj, то наш средний выигрыш будет равен

Так как мф применяем 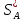, то наш средний выигрыш не может быть меньше цены игры 𝛄, т.е. a_j>𝛄, j = 1, 2, …, n, поэтому

………………

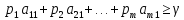
(1)

СТРОКИ ВЫШЕПЕРЕЧИСЛЕННОЙ СИСТЕМЫ ПИШЕТСЯ ПО СТОЛБЦАМ МАТРИЦЫ ИГРЫ

Разделим все получившиеся на положительную величину 𝛄 и введем обозначения

x₁ = p₁/𝛄, x₂ = p₂/𝛄, …, x_m = p_m/𝛄.

Тогда система (1) превращается в следующую

………………

(2)

Так как р₁+р₂+…+p_m=1, то

x₁+x₂+…+x_m=1/𝛄.

Мы хотим сделать наш гарантированный выигрыш максимально возможным. При этом величина 1/𝛄 принимает минимальное значение.

Мы получаем следующую задачу линейного программирования: найти такие неотрицательные значения x₁, x₂, …, x_m, которые удовлетворяли бы линейным ограничениям (2) и обращали бы в минимум линейную функцию

L = x₁+x₂+…+x_m

Решив эту задачу линейного программирования, мы можем найти оптимальную стратегию игрока А.

Нахождение . Оптимальная стратегия находится аналогично. Разница заключается в том, что игрок В стремится не максимизировать, а минимизировать выигрыш, а значить максимизировать величину 1/𝛄. Следовательно, вместо условий (2) должны соблюдаться условия

………………

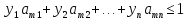(3)

где y_j = q_j/ 𝛄, j = 1, 2, …, n.

Требуется так выбрать неотрицательные значения переменных y1, y2, …, yn, чтобы они удовлетворяли условиям (3) и обращали в максимум линейную функцию

L = y₁ + y₂ + … + y_n = 1/𝛄

или, что то же самое, обращали в минимум линейную функцию

L =y₁ y₂ … y_n = 1/𝛄

Таким образом, любая конечная игра nxm сводится к задачам линейного программирования.

Возможно, сюда еще надо будет вписать первую часть (теорию) из пункта 3.2., который идет дальше