
- •1) Методы принятия оптимальных решений. Математические модели операции: детерминированный случай, оптимизация решений в условиях неопределенности.
- •1) Детерминированный случай
- •2) Оптимизация решений в условиях неопределенности
- •2) Методы принятия оптимальных решений. Оценка операции по нескольким показателям.
- •3) Оценка операции по нескольким показателям.
- •3) Основная задача линейного программирования (озлп). Допустимые решения и оптимальное решение задачи лп.
- •4) Геометрическая интерпретация озлп.
- •Анализ положения l относительно одр.
- •Дадим геометрическую интерпретацию поиска оптимального решения.
- •Тогда (x1*, x2*, …, xn*) – оптимальное решение
- •Некоторые выводы
- •5) Задача лп с ограничениями-неравенствами. Переход от нее к основной задаче.
- •6) Симплекс-метод решения задачи лп.
- •7) Табличный алгоритм замены переменных.
- •8. Отыскание опорного решения задачи лп на основе табличного алгоритма замены переменных.
- •9. Отыскание оптимального решения задачи лп на основе табличного алгоритма замены переменных.
- •10. Метод динамического программирования (дп). Алгоритм решения задач управления состоянием организма в биотехнических системах. Основное рекуррентное уравнение дп.
- •11. Управление переходом организма из исходного в конечное состояние методом дп: использование ориентированного графа.
- •12. Управление переходом организма из исходного состояния в конечное в условиях неопределенности.
- •13. Игровые методы обоснования решений. Основные понятия теории игр. Платежная матрица.
- •14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.
- •15. Решение игры в смешанных стратегиях.
- •16. Игры 2х2 и их решение.
- •17. Геометрическая интерпретация решений игры 2х2.
- •18. Решение игр 2хn.
- •19. Решение игр mх2.
- •20. Решение игр mxn.
- •3.2. Элементы теории статистических решений
1) Методы принятия оптимальных решений. Математические модели операции: детерминированный случай, оптимизация решений в условиях неопределенности.
Операция – любое мероприятие (система действий), объединенных единим замыслом и направленных к достижению определенной цели.
– всегда управляемое мероприятие (т.е. от нас зависит, какие параметры выбрать и как организовать).
– определенный выбор параметров составляет решение
Основная задача исследование операции – предварительное количественное обоснование оптимальных решений.
Раз мы говорим об оптимизации, то необходимо операции сопоставить функцию эффективности.
Эффективность – степень приспособленности к выполнению задачи, стоящей перед ней. Чем лучше организована операция, тем она более эффективна.
В исследовании операций вводят показатель эффективности или целевую функцию (ЦФ). Как правило, ЦФ определяется моделью операции, а модель операции, в свою очередь, определяет круг методов оптимизации.
Основные математические модели операций.
1) Детерминированный случай
Предположим, что модель операции известна. Она позволяет вычислить значения целевой функции при всяком (различном) принятом решении.
w = w (α1, α2, …, x1, x2, …), где αi – некоторые известные факторы, на которые мы влиять не можем;
xi – элементы решения, т.е. зависящие от нас факторы.
Параметры α могут быть числа, функции, различные ограничения, которые накладываются на x.
Параметры x могут быть либо числа, либо функции.
Для такой модели возникает класс вариационных задач.
– Если известно аналитическое выражение w, то используются поисковые методы для обнаружения экстремумов функции.
– Если вид функции не известен (т.е. нет формулы), то используются следующие поисковые методы:
– метод перебора;
– метод пропорционального поиска;
– градиентный метод.
Если α – линейные ограничения на элементы решения xi, то чаще используют методы линейного программирования.
Если исследуется динамика некоторой системы, т.е. развитие ее состояния во времени и удается выделить некоторые промежуточные состояния системы, то используют методы динамического программирования.
2) Оптимизация решений в условиях неопределенности
Предположим, что модель операции известна. Она позволяет вычислить значения целевой функции при всяком (различном) принятом решении.
w = w (α1, α2, …, y1, y2, …, x1, x2, …),
где αi – некоторые известные факторы, на которые мы влиять не можем;
xi – элементы решения, т.е. зависящие от нас факторы;
yi – неизвестные фактора (условия) проведения операции.
Применяемые методы зависят от природы yi.
– Если yi – параметры, обладающие статистической устойчивостью (подчиняются некоторым статистическим законам распределения), тогда
yi
заменяются на средние
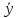 и применяются методы, что и в
детерминированных случаях или используют
оптимизацию в среднем.
и применяются методы, что и в
детерминированных случаях или используют
оптимизацию в среднем.
Оптимизация
в среднем
– процедура нахождения wmax
заменяется на нахождение
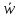 max.
max.
– Если параметры yi не подчиняются законам (т.е. меняются хаотично), то находят множество локально оптимальных решений. В результате их анализа выбирается наилучшее решение, но оно не будет строго оптимальным. – yi зависят не от объективных обстоятельств, а от активно противодействующий (т.е. противника). В боевых действиях, спортивных соревнованиях, конкурентной борьбе, т.е. в конфликтных ситуациях. В данном случае применяется теория игр, учитывающая, что «противник» ведет себя наихудшим образом для нас.
